- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему ЕГЭ по математике 2016. Решение геометрических задач.
Содержание
- 1. ЕГЭ по математике 2016. Решение геометрических задач.
- 2. «Если хотите научиться плавать,то смело входите в
- 3. Заявленное авторами содержание К каждому контрольно-измерительному
- 4. Проверяемые умения«Спецификация КИМ – 2016(профильный)»:«Уметь выполнять действия
- 5. О чём в действительности эта задача?Суть задачи:
- 6. Рассмотрим несколько задач из федерального банка заданий,
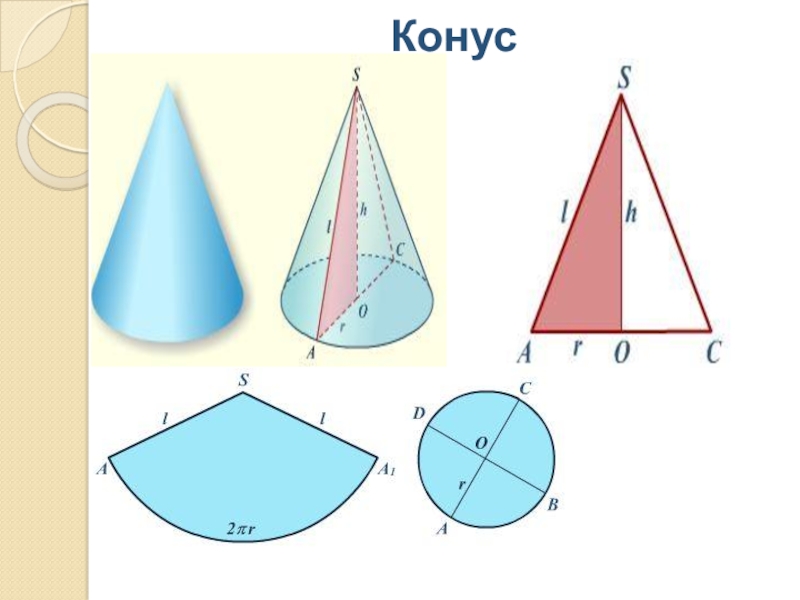
- 7. Конус
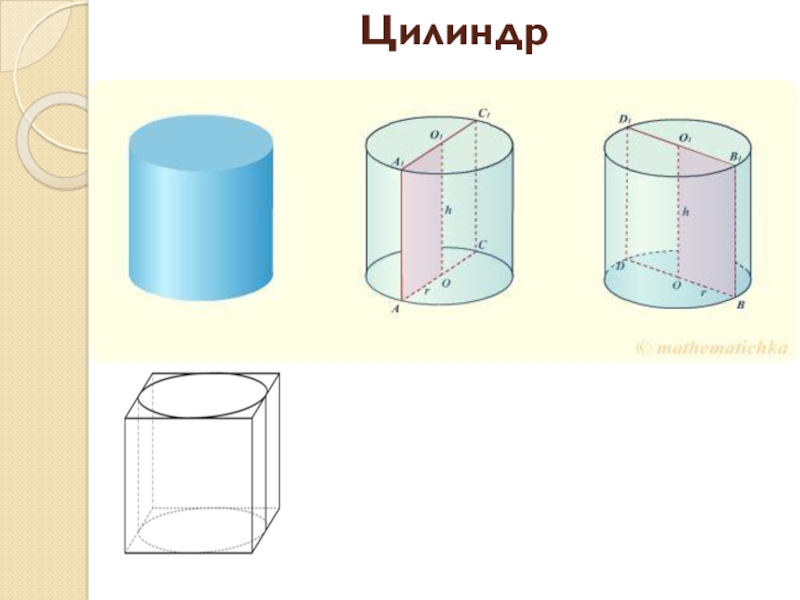
- 8. Цилиндр
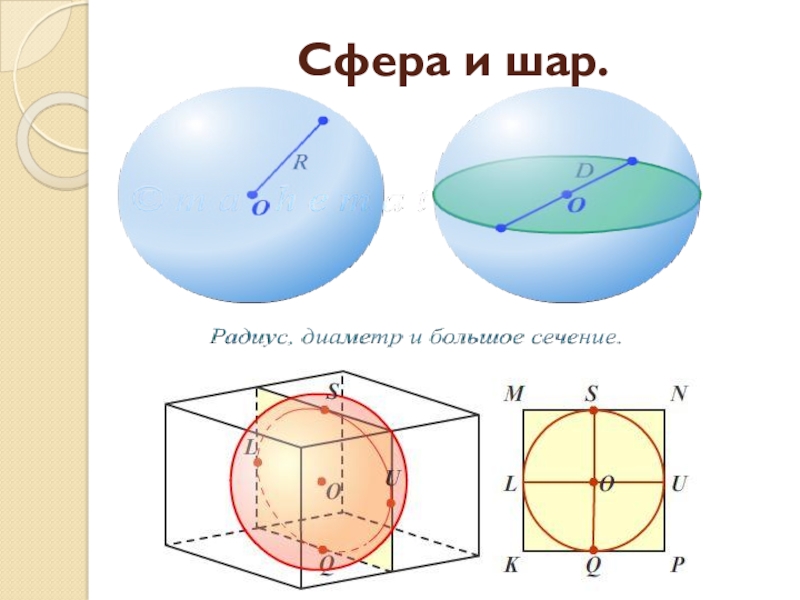
- 9. Сфера и шар.
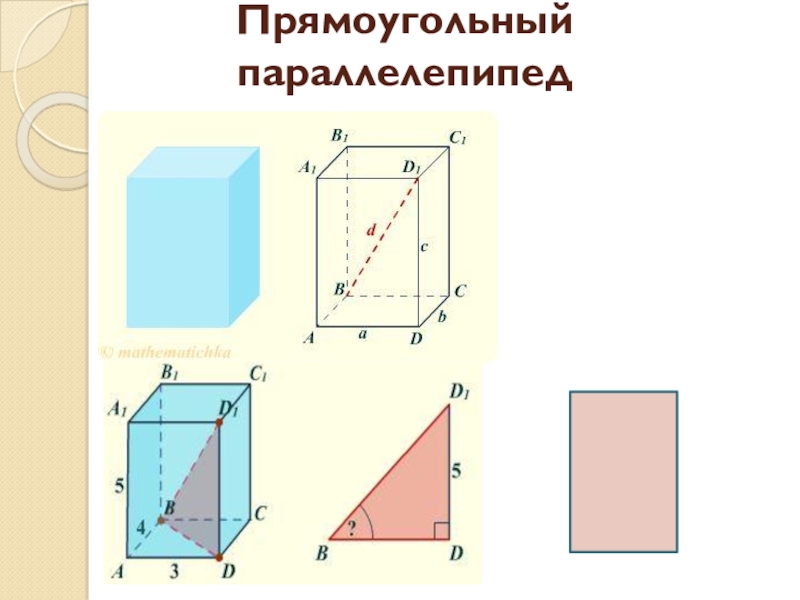
- 10. Прямоугольный параллелепипед
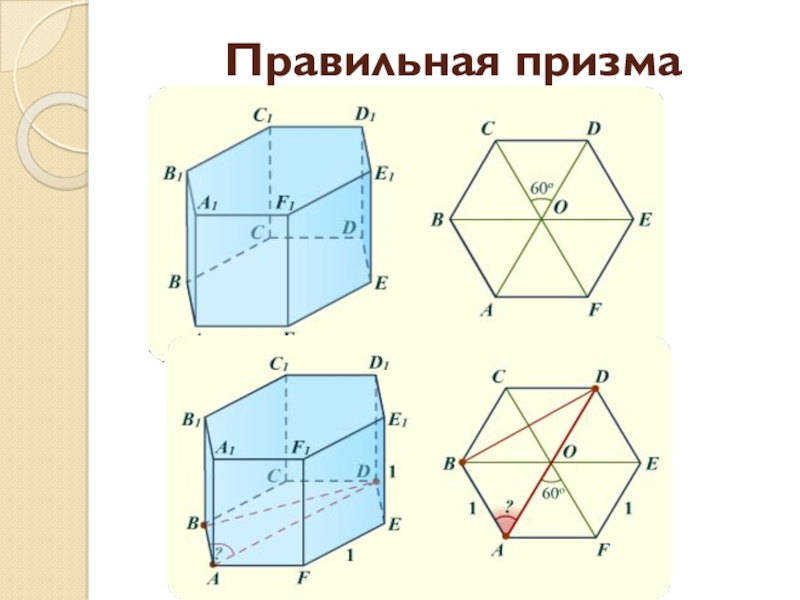
- 11. Правильная призма
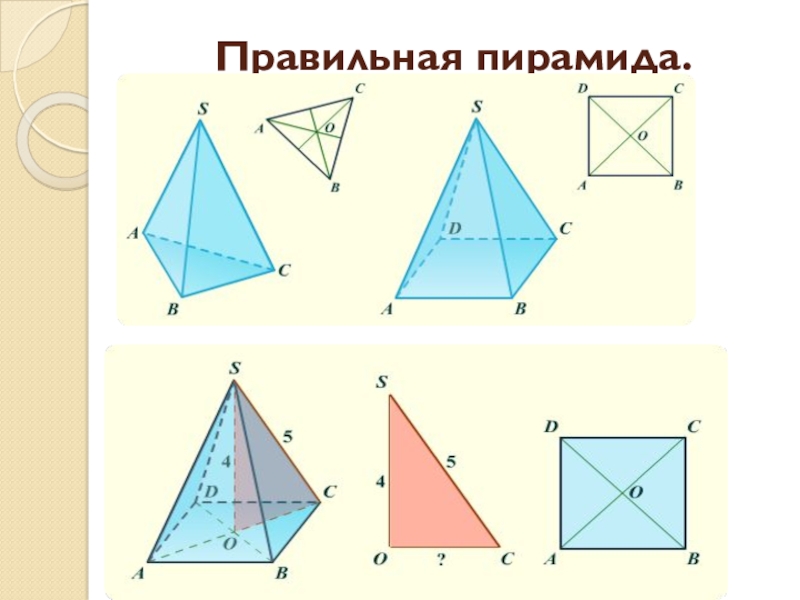
- 12. Правильная пирамида.
- 13. Теоретическая базаОБЪЁМЫ ТЕЛ:
- 14. Теоретическая базаОБЪЁМЫ ТЕЛ:
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Алгоритм решения задач: 1. Чертим фигуру. Не
- 19. Задача 1 Высота конуса равна 4,
- 20. Задача 2. Высота конуса равна 4, а
- 21. Задача 3 Диаметр основания конуса равен 6,
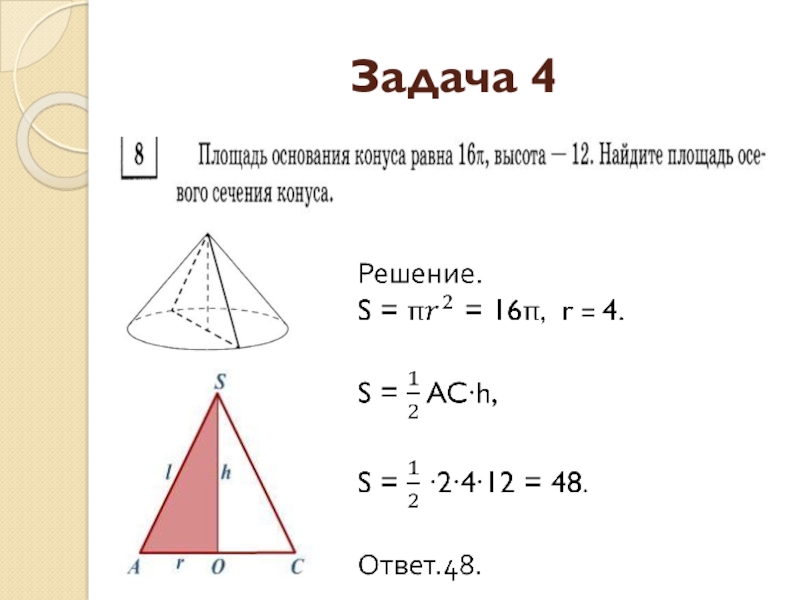
- 22. Задача 4
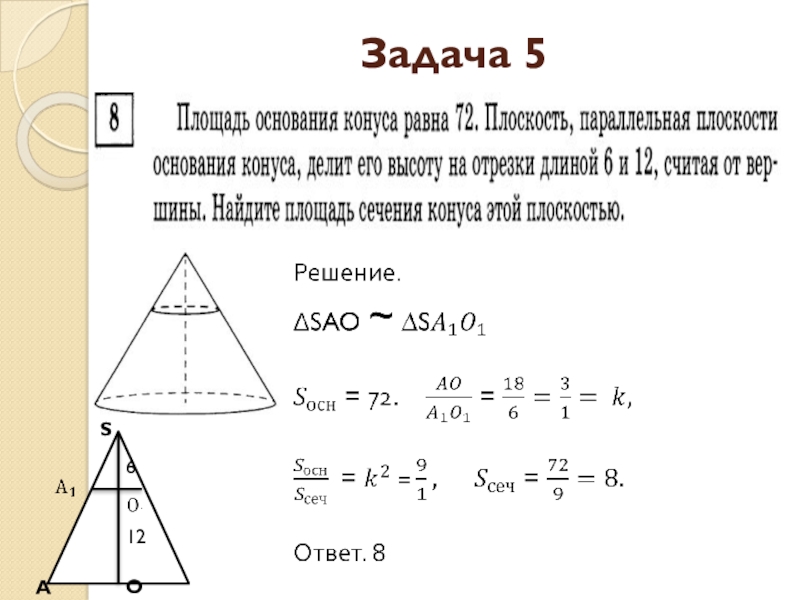
- 23. Задача 5А126ОS
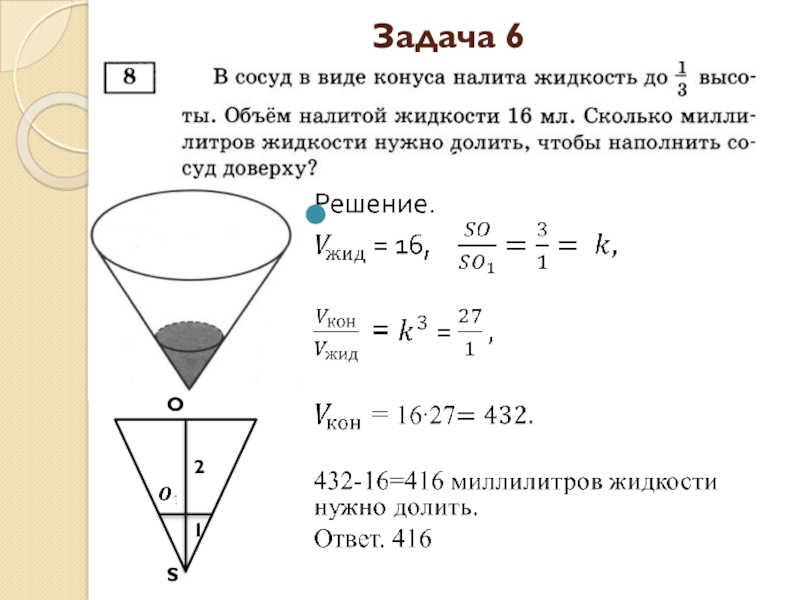
- 24. Задача 612SO
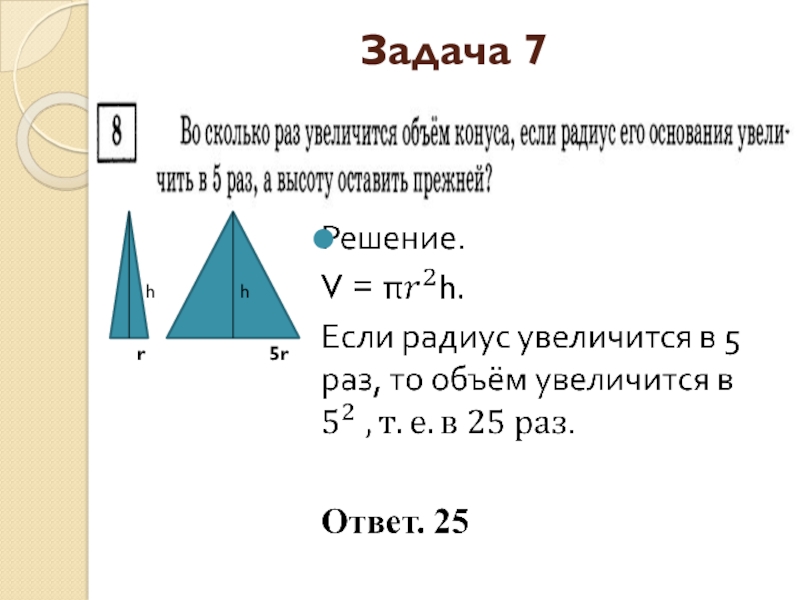
- 25. Задача 7r5rhh
- 26. Задача 8
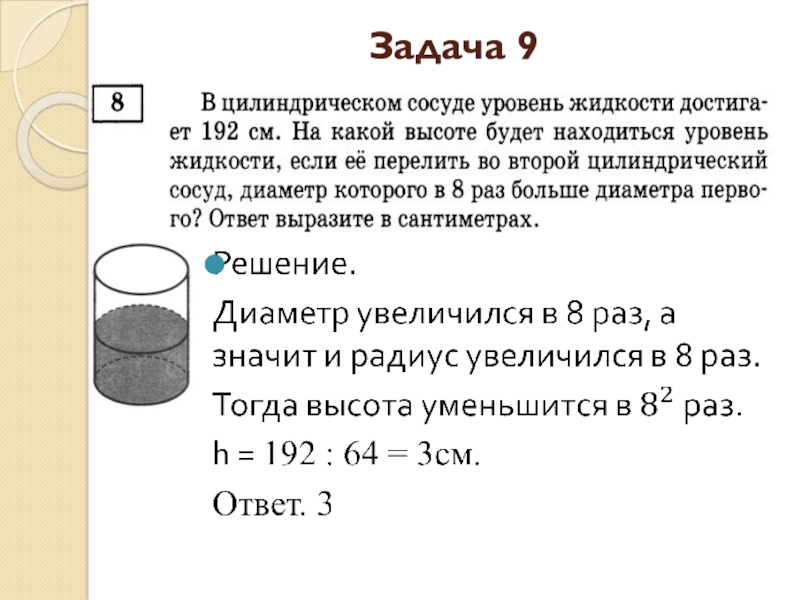
- 27. Задача 9
- 28. Задача 102211
- 29. Задача 11
- 30. Задача 12
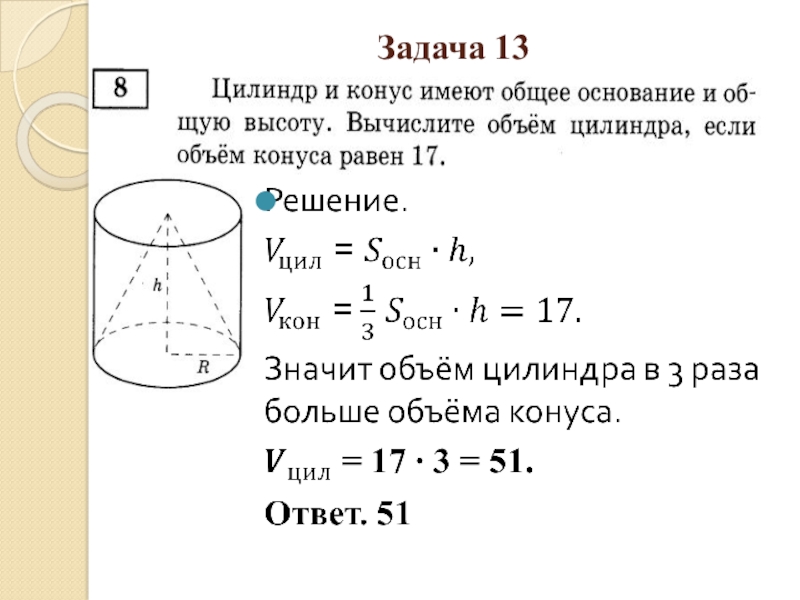
- 31. Задача 13
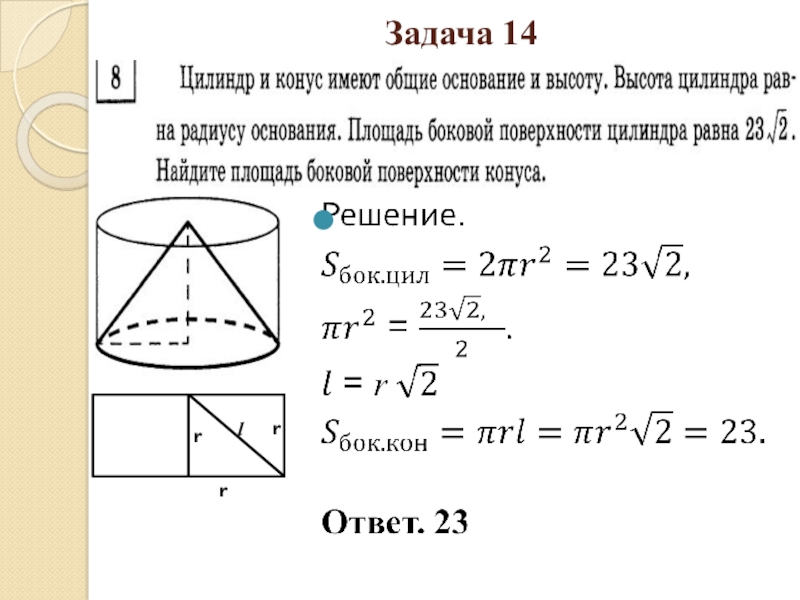
- 32. Задача 14rrrl
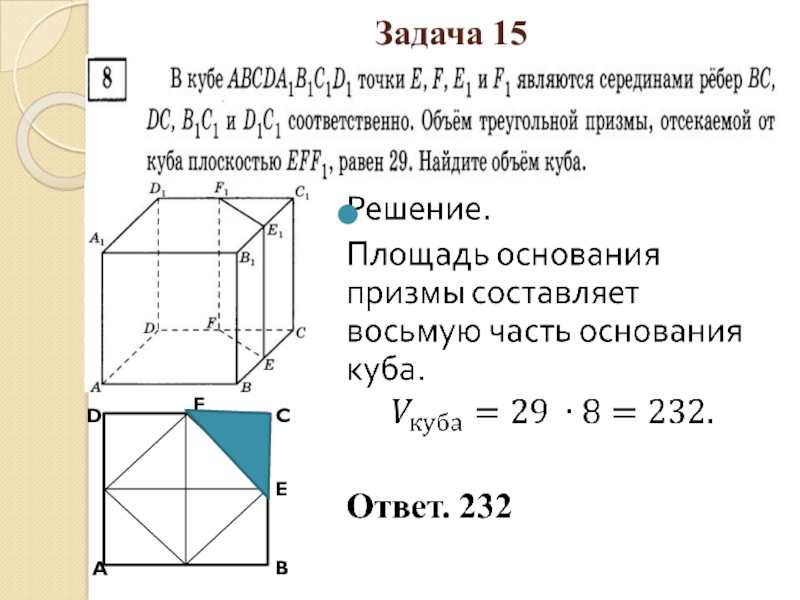
- 33. Задача 15АВСDFE
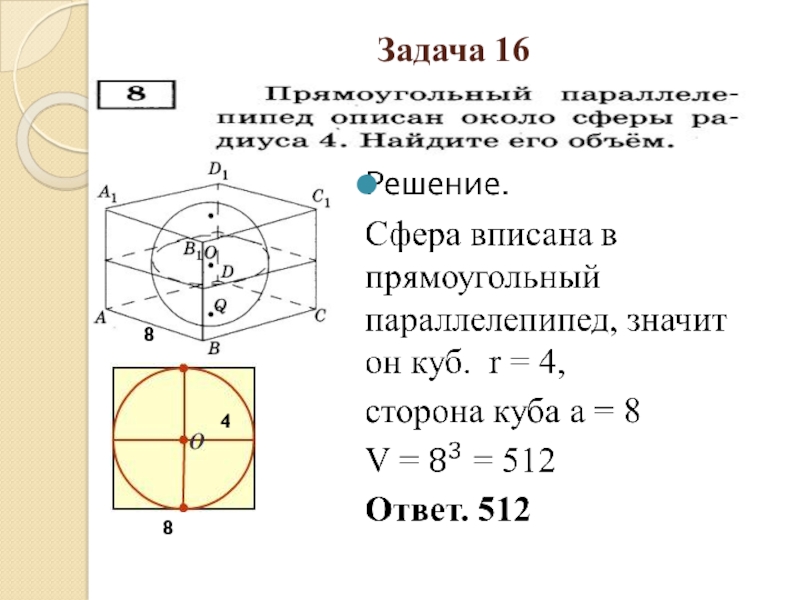
- 34. Задача 16488
- 35. Задача 17
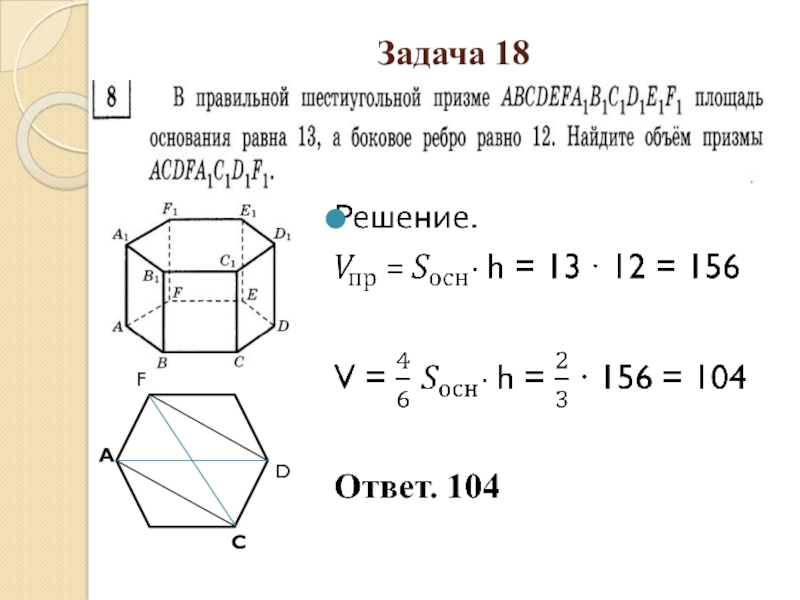
- 36. Задача 18АСDF
- 37. Методические рекомендацииВнимательное построение параллельной проекции стереометрической фигуры
- 38. ВыводИтак, мы научились решать стереометрические задачи. Но
- 39. Спасибо за внимание !
«Если хотите научиться плавать,то смело входите в воду, а если хотите научиться решать задачи, то решайте их» Д. Пойа
Слайд 1ЕГЭ по математике 2016
Задача № 8
Профильный уровень
МБОУ Крюковская СОШ
Учитель математики: Угроватова
Т.В.
Слайд 2«Если хотите научиться плавать,
то смело входите в воду, а если хотите
научиться решать задачи,
то решайте их»
Д. Пойа
то решайте их»
Д. Пойа
Слайд 3Заявленное авторами содержание
К каждому контрольно-измерительному материалу (КИМ) ЕГЭ авторы
предоставляют полный набор сопровождающей документации:
Спецификацию контрольно-измерительных материалов 2016,
Кодификатор требований к уровню подготовки выпускников образовательных организаций 2016
Кодификатор элементов содержания по математике 2016
Спецификацию контрольно-измерительных материалов 2016,
Кодификатор требований к уровню подготовки выпускников образовательных организаций 2016
Кодификатор элементов содержания по математике 2016
Слайд 4Проверяемые умения
«Спецификация КИМ – 2016(профильный)»:
«Уметь выполнять действия с геометрическими фигурами, координатами
и векторами»
Детализация проверяемых умений.
«Кодификатор требований КИМ 2016 (КТ)»
Проверяемые элементы содержания.
«Кодификатор элементов содержания КИМ 2016 (КЭС)»
П. 5.2 «Прямые и плоскости в пространстве»
П.5.3 «Многогранники»
П.5.4 «Тела и поверхности вращения»
П. 5.5 «Измерение геометрических величин»
Детализация проверяемых умений.
«Кодификатор требований КИМ 2016 (КТ)»
Проверяемые элементы содержания.
«Кодификатор элементов содержания КИМ 2016 (КЭС)»
П. 5.2 «Прямые и плоскости в пространстве»
П.5.3 «Многогранники»
П.5.4 «Тела и поверхности вращения»
П. 5.5 «Измерение геометрических величин»
4.2
Решать простейшие геометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении стереометрических задач планиметрические факты и методы.
Слайд 5О чём в действительности эта задача?
Суть задачи: определение объёмов многогранников и
тел вращения, умение производить операции с объёмами (сравнение, вычитание, сложение).
Типы задач №8.
Нахождение объёмов вписанных и описанных фигур.
Нахождение объёмов составных фигур.
Сравнение объёмов двух фигур по известному соотношению их элементов.
Задача с переливанием жидкости из одного сосуда в другой.
Типы задач №8.
Нахождение объёмов вписанных и описанных фигур.
Нахождение объёмов составных фигур.
Сравнение объёмов двух фигур по известному соотношению их элементов.
Задача с переливанием жидкости из одного сосуда в другой.
Слайд 6Рассмотрим несколько задач из федерального банка заданий, сгруппировав их по типам
тел.
Конус.
Цилиндр.
Шар и сфера.
Прямоугольный параллелепипед
Правильная призма.
Правильная пирамида.
Многогранник
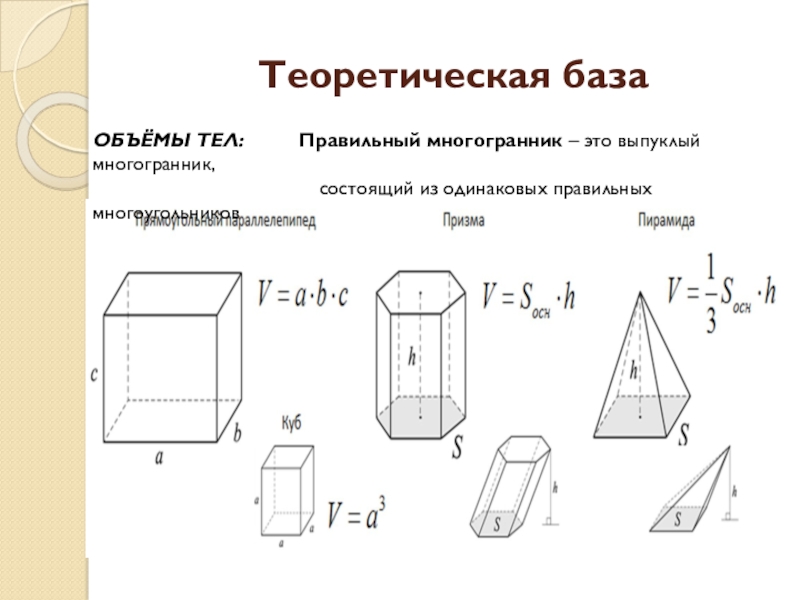
Слайд 13Теоретическая база
ОБЪЁМЫ ТЕЛ: Правильный многогранник – это
выпуклый многогранник,
состоящий из одинаковых правильных многоугольников
состоящий из одинаковых правильных многоугольников
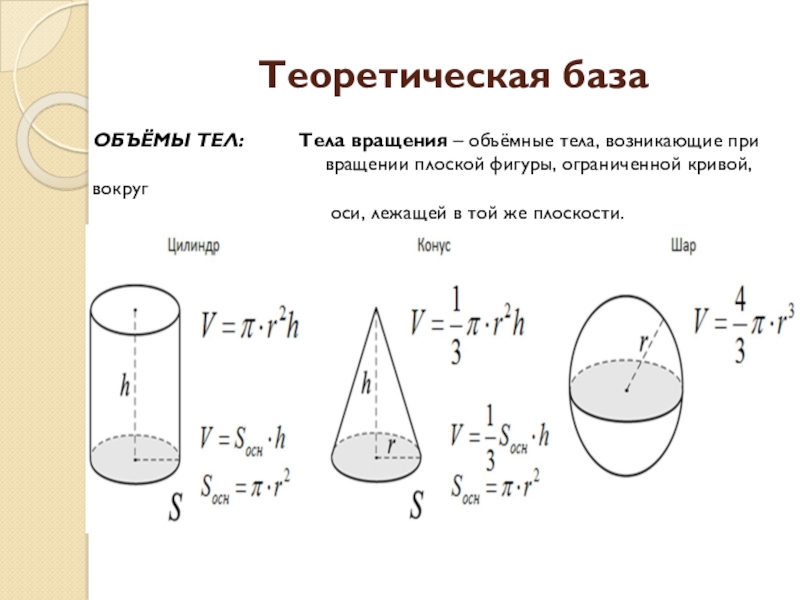
Слайд 14Теоретическая база
ОБЪЁМЫ ТЕЛ: Тела вращения – объёмные
тела, возникающие при
вращении плоской фигуры, ограниченной кривой, вокруг
оси, лежащей в той же плоскости.
вращении плоской фигуры, ограниченной кривой, вокруг
оси, лежащей в той же плоскости.
Слайд 18Алгоритм решения задач:
1. Чертим фигуру. Не обязательно в масштабе, можно
от
руки. 2. Подписываем вершины. Отмечаем на чертеже
упомянутые в условии точки. Соединяем линиями, где
это необходимо. 3. Ставим известные (заданные) значения прямо на
чертеже. 4. Если получился треугольник внутри тела, то выясняем
есть ли в нем прямой угол и какой именно. Для этого
пользуемся теоремами о перпендикуляре к плоскости
или о трех перпендикулярах. 5. Чертим этот треугольник на плоскости. На нем также
отмечаем заданные и искомые величины, если нужно,
перенося числа с параллельных ребер. 6. Проводим необходимые вычисления по известным
формулам. Как правило, это будут теорема Пифагора и
определения синуса и косинуса острых углов
прямоугольного треугольника.
руки. 2. Подписываем вершины. Отмечаем на чертеже
упомянутые в условии точки. Соединяем линиями, где
это необходимо. 3. Ставим известные (заданные) значения прямо на
чертеже. 4. Если получился треугольник внутри тела, то выясняем
есть ли в нем прямой угол и какой именно. Для этого
пользуемся теоремами о перпендикуляре к плоскости
или о трех перпендикулярах. 5. Чертим этот треугольник на плоскости. На нем также
отмечаем заданные и искомые величины, если нужно,
перенося числа с параллельных ребер. 6. Проводим необходимые вычисления по известным
формулам. Как правило, это будут теорема Пифагора и
определения синуса и косинуса острых углов
прямоугольного треугольника.
Слайд 19Задача 1
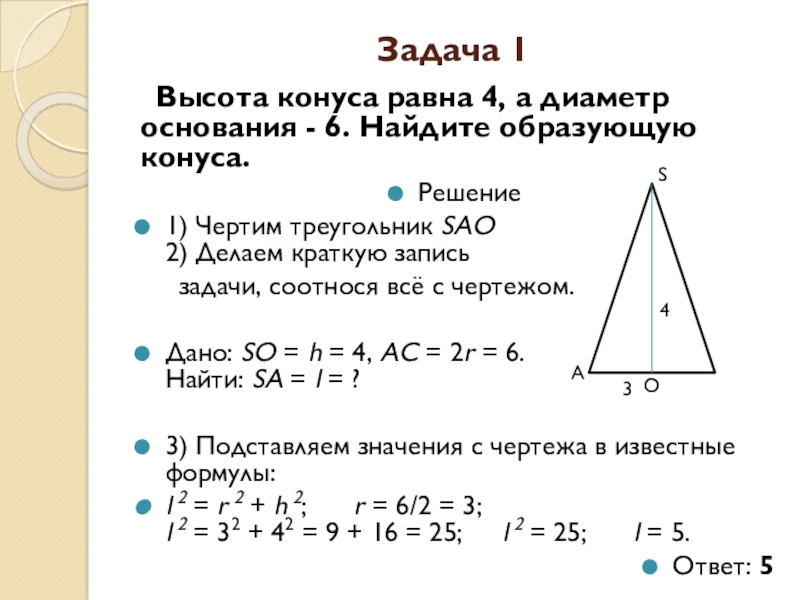
Высота конуса равна 4, а диаметр основания - 6.
Найдите образующую конуса.
Решение
1) Чертим треугольник SAO 2) Делаем краткую запись
задачи, соотнося всё с чертежом.
Дано: SO = h = 4, AC = 2r = 6. Найти: SA = l = ?
3) Подставляем значения с чертежа в известные формулы:
l 2 = r 2 + h 2; r = 6/2 = 3; l 2 = 32 + 42 = 9 + 16 = 25; l 2 = 25; l = 5.
Ответ: 5
Решение
1) Чертим треугольник SAO 2) Делаем краткую запись
задачи, соотнося всё с чертежом.
Дано: SO = h = 4, AC = 2r = 6. Найти: SA = l = ?
3) Подставляем значения с чертежа в известные формулы:
l 2 = r 2 + h 2; r = 6/2 = 3; l 2 = 32 + 42 = 9 + 16 = 25; l 2 = 25; l = 5.
Ответ: 5
S
A
O
4
3
Слайд 20Задача 2.
Высота конуса равна 4, а длина образующей - 5. Найдите
диаметр основания конуса.
Решение
Порядок наших действий такой же, как в предыдущей задаче: чертеж, краткая запись, формулы. Только в конце неизвестная величина оказывается в правой части равенства, что несколько удлиняет вычисления.
SO = h = 4, SA = l = 5, AC = 2r = ? l 2 = r 2 + h 2; 52 = r 2 + 42; 52 − 42 = r 2 или r 2 = 52 − 42 = 25 − 16 = 9; r 2 = 9; r = 3; AC = 2r = 2×3 = 6.
Ответ. 6
Решение
Порядок наших действий такой же, как в предыдущей задаче: чертеж, краткая запись, формулы. Только в конце неизвестная величина оказывается в правой части равенства, что несколько удлиняет вычисления.
SO = h = 4, SA = l = 5, AC = 2r = ? l 2 = r 2 + h 2; 52 = r 2 + 42; 52 − 42 = r 2 или r 2 = 52 − 42 = 25 − 16 = 9; r 2 = 9; r = 3; AC = 2r = 2×3 = 6.
Ответ. 6
Слайд 21Задача 3
Диаметр основания конуса равен 6, а длина образующей - 5.
Найдите высоту конуса.
Решение
См. пояснения к предыдущим задачам. AC = 2r = 6, SA = l = 5, SO = h = ? l 2 = r 2 + h 2; r = 6/2 = 3; 52 = 32 + h 2; 52 − 32 = h 2 или h 2 = 52 − 32 = 25 − 9 = 16; h 2 = 16; h = 4.
Ответ. 4
Решение
См. пояснения к предыдущим задачам. AC = 2r = 6, SA = l = 5, SO = h = ? l 2 = r 2 + h 2; r = 6/2 = 3; 52 = 32 + h 2; 52 − 32 = h 2 или h 2 = 52 − 32 = 25 − 9 = 16; h 2 = 16; h = 4.
Ответ. 4
Слайд 37Методические рекомендации
Внимательное построение параллельной проекции стереометрической фигуры в черновике (изображение как
самой фигуры, так и её плоских сечений)
Предварительный анализ чертежа для поиска правильного хода решения
Пространственное мышление
Знание формул вычисления объёмов и площадей(умение вывести нужную формулу при необходимости)
Хорошее знание планиметрии
Контроль результата с учётом искажений проекции тела
При параллельном проектировании не сохраняются углы, длины отрезков и соотношения длин сторон, лежащие в разных плоскостях.
Сайт. http://mathematichka.ru
Предварительный анализ чертежа для поиска правильного хода решения
Пространственное мышление
Знание формул вычисления объёмов и площадей(умение вывести нужную формулу при необходимости)
Хорошее знание планиметрии
Контроль результата с учётом искажений проекции тела
При параллельном проектировании не сохраняются углы, длины отрезков и соотношения длин сторон, лежащие в разных плоскостях.
Сайт. http://mathematichka.ru
!
Слайд 38Вывод
Итак, мы научились решать стереометрические задачи. Но то, что мы посмотрели,
это лишь капля в море. Для того, чтобы уметь хорошо решать задачи надо прежде всего много сидеть самому.