- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Детская презентация по математике Симметрия в природе
Содержание
- 1. Детская презентация по математике Симметрия в природе
- 2. Симме́три́я (др. греч. συμμετρία «соразмерность», от μετρέω — «меряю»), в широком
- 3. типы симметрии в природе :ПОВОРОТНАЯ
- 4. Свойственная большинству цветов поворотная симметрия n-го порядка
- 5. Например, для цветка молочая n=2, он совмещается сам с собой при повороте на углы 180 и 360.
- 6. Для триллиума и ириса n=3, а подходящие углы поворота-120, 240, 360.
- 7. Нередко встречаются цветы с поворотной симметрий 4-го порядка (сирень, чистотел)
- 8. 6-го порядка (лилия, шафран)
- 9. и более высокого порядка, но особенно часто – 5-го (герань, лютик )
- 10. ЗЕРКАЛЬНАЯ СИММЕТРИЯ. Зеркально симметричным считается объект, состоящий
- 11. Подсолнухи могут похвастаться радиальной симметрией и интересным
- 12. Большинство животных имеют двустороннюю симметрию, что означает,
- 13. Есть около 5000 типов пауков, и все
- 14. Даже такие крошечные образования, как снежинки, регулируются
- 15. Как мы уже видели, симметрия и математические
- 16. Если учесть, что Солнце имеет диаметр 1,4
- 17. На протяжении тысяч лет люди удивлялись идеальной
- 18. На протяжении веков симметрия остается предметом, который
- 19. Слайд 19
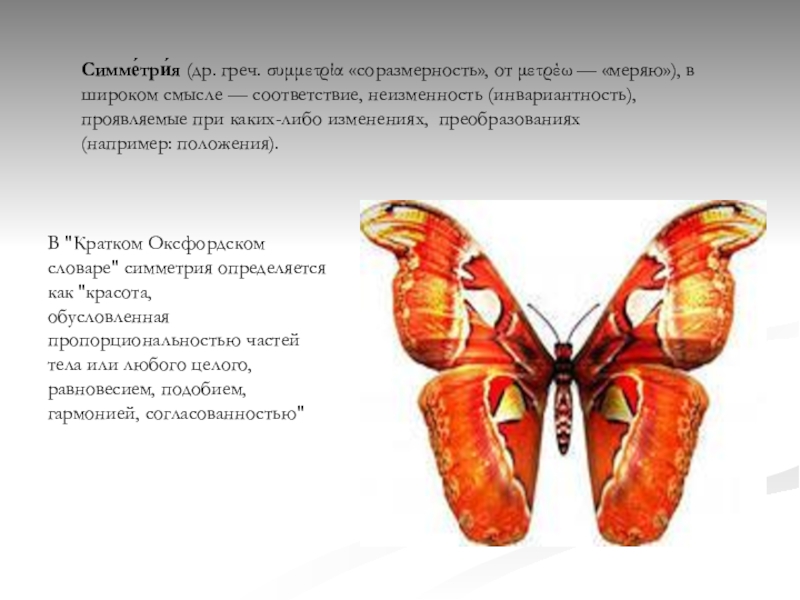
Симме́три́я (др. греч. συμμετρία «соразмерность», от μετρέω — «меряю»), в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях(например: положения).В "Кратком Оксфордском словаре" симметрия определяется как "красота,обусловленная пропорциональностью частей тела или любого целого,равновесием, подобием, гармонией, согласованностью"
Слайд 2Симме́три́я (др. греч. συμμετρία «соразмерность», от μετρέω — «меряю»), в широком смысле — соответствие, неизменность (инвариантность),
проявляемые при каких-либо изменениях, преобразованиях(например: положения).
В "Кратком Оксфордском словаре" симметрия определяется как "красота,
обусловленная пропорциональностью частей тела или любого целого,
равновесием, подобием, гармонией, согласованностью"
Слайд 3типы симметрии в природе :
ПОВОРОТНАЯ СИММЕТРИЯ.
2) ПЕРЕНОСНАЯ (СКОЛЬЗЯЩАЯ)
СИММЕТРИЯ.
3) ЗЕРКАЛЬНАЯ СИММЕТРИЯ.
4) СИММЕТРИИ ПОДОБИЯ И ДР.
3) ЗЕРКАЛЬНАЯ СИММЕТРИЯ.
4) СИММЕТРИИ ПОДОБИЯ И ДР.
Слайд 4Свойственная большинству цветов поворотная симметрия n-го порядка проявляется в том, что
цветок совмещается сам с собой при повороте вокруг своей оси на любой из углов, где n>1, k=1,2,3…,n.
Слайд 10ЗЕРКАЛЬНАЯ СИММЕТРИЯ. Зеркально симметричным считается объект, состоящий из двух половин, которые
являются зеркальными двойниками по отношению друг к другу.
Слайд 11Подсолнухи могут похвастаться радиальной симметрией и интересным типом симметрии, известной как
последовательность Фибоначчи. Последовательность Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д. (каждое число определяется суммой двух предыдущих чисел). Если бы мы не спешили и подсчитали количество семян в подсолнухе, то мы бы обнаружили, что количество спиралей растет по принципам последовательности Фибоначчи. В природе есть очень много растений (в том числе и брокколи романеско), лепестки, семена и листья которых отвечают этой последовательности, поэтому так трудно найти клевер с четырьмя листочками.
Слайд 12Большинство животных имеют двустороннюю симметрию, что означает, что они могут быть
разделены на две одинаковых половинки. Даже люди обладают двусторонней симметрией, и некоторые ученые полагают, что симметрия человека является наиболее важным фактором, который влияет на восприятие нашей красоты.
Слайд 13Есть около 5000 типов пауков, и все они создают почти идеальное
круговое полотно с радиальными поддерживающими нитями почти на равном расстоянии и спиральной тканью для ловли добычи. Ученые не уверены, почему пауки так любят геометрию, так как испытания показали, что круглое полотно не заманит еду лучше, чем полотно неправильной формы. Ученые предполагают, что радиальная симметрия равномерно распределяет силу удара, когда жертва попадает в сети, в результате чего получается меньше разрывов.
Слайд 14Даже такие крошечные образования, как снежинки, регулируются законами симметрии, так как
большинство снежинок имеет шестигранную симметрию. Это происходит в частности из-за того, как молекулы воды выстраиваются, когда затвердевают (кристаллизуются). Молекулы воды приобретают твердое состояние, образуя слабые водородные связи, они выравниваются в упорядоченном расположении, которое уравновешивает силы притяжения и отталкивания, формируя гексагональную форму снежинки. Но при этом каждая снежинка симметрична, но ни одна снежинка не похожа на другую. Это происходит потому, что падая с неба, каждая снежинка испытывает уникальные атмосферные условия, которые заставляют её кристаллы располагаться определенным образом.
Слайд 15Как мы уже видели, симметрия и математические модели существуют почти везде,
но разве эти законы природы ограничиваются нашей планетой? Очевидно, нет. Недавно открыли новую секцию на краю Галактики Млечного Пути, и астрономы считают, что галактика представляет собой почти идеальное зеркальное отражение себя.
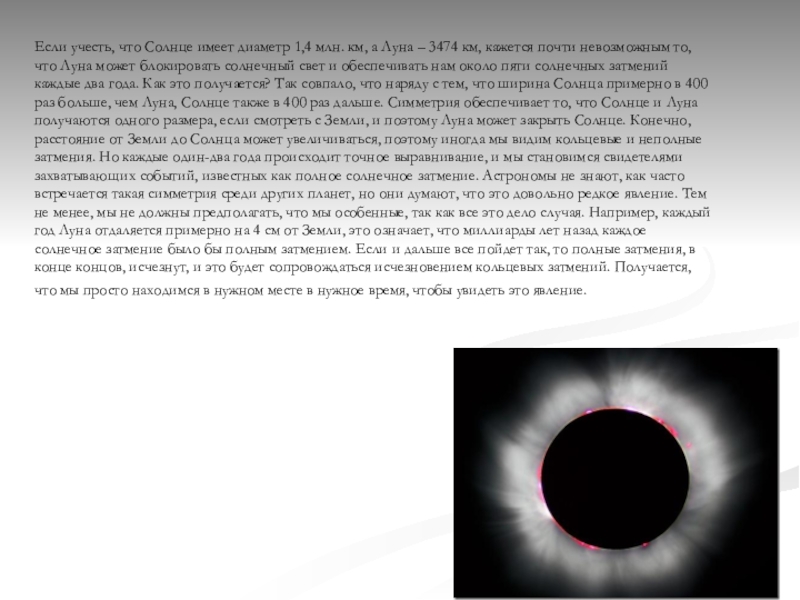
Слайд 16Если учесть, что Солнце имеет диаметр 1,4 млн. км, а Луна
– 3474 км, кажется почти невозможным то, что Луна может блокировать солнечный свет и обеспечивать нам около пяти солнечных затмений каждые два года. Как это получается? Так совпало, что наряду с тем, что ширина Солнца примерно в 400 раз больше, чем Луна, Солнце также в 400 раз дальше. Симметрия обеспечивает то, что Солнце и Луна получаются одного размера, если смотреть с Земли, и поэтому Луна может закрыть Солнце. Конечно, расстояние от Земли до Солнца может увеличиваться, поэтому иногда мы видим кольцевые и неполные затмения. Но каждые один-два года происходит точное выравнивание, и мы становимся свидетелями захватывающих событий, известных как полное солнечное затмение. Астрономы не знают, как часто встречается такая симметрия среди других планет, но они думают, что это довольно редкое явление. Тем не менее, мы не должны предполагать, что мы особенные, так как все это дело случая. Например, каждый год Луна отдаляется примерно на 4 см от Земли, это означает, что миллиарды лет назад каждое солнечное затмение было бы полным затмением. Если и дальше все пойдет так, то полные затмения, в конце концов, исчезнут, и это будет сопровождаться исчезновением кольцевых затмений. Получается, что мы просто находимся в нужном месте в нужное время, чтобы увидеть это явление.
Слайд 17На протяжении тысяч лет люди удивлялись идеальной гексагональной форме сот и
спрашивали себя, как пчелы могут инстинктивно создать форму, которую люди могут воспроизвести только с помощью циркуля и линейки. Как и почему пчелы имеют страстное желание создавать шестиугольники? Математики считают, что это идеальная форма, которая позволяет им хранить максимально возможное количество меда, используя минимальное количество воска. В любом случае, все это продукт природы, и это чертовски впечатляет.
Слайд 18На протяжении веков симметрия остается предметом, который очаровывает философов, астрономов, математиков,
художников, архитекторов и физиков. Древние греки были совершенно одержимы ею – и даже сегодня мы, как правило, сталкиваемся с симметрией во всем от планирования расположения нашей мебели до стрижки волос.