- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Четырехугольники
Содержание
- 1. Четырехугольники
- 2. МногоугольникиМногоугольникВыпуклый многоугольникЧетырёхугольникПараллелограмм и трапецияПараллелограммСвойства параллелограммаПризнаки параллелограммаТрапецияТеорема ФалесаПрямоугольник, ромб, квадратПрямоугольникРомб и квадратОсевая и центральная симметрииРАССМАТРИВАЕМЫЕ ВОПРОСЫ
- 3. МНОГОУГОЛЬНИК Рассмотрим фигуру, составленную из отрезков АВ, ВС,
- 4. Обрати внимание! Фигура, изображенная на рисунке 3, не
- 5. Две вершины многоугольника, принадлежащие одной стороне, называются
- 6. Выпуклый многоугольник Многоугольник называется выпуклым, если он
- 7. Выпуклый многоугольник Для этого соединим диагоналями вершину А1
- 8. Четырёхугольник Каждый четырехугольник имеет четыре вершины, четыре стороны
- 9. ПараллелограммОпределениеПараллелограммом называется четырехугольник, у которого противоположные стороны
- 10. 2°. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть
- 11. Признаки параллелограммаРассмотрим три признака параллелограмма.1°. Если в
- 12. 2°. Если в четырехугольнике противоположные стороны попарно
- 13. Трапеция Трапецией называется четырехугольник, у которого две стороны
- 14. Теорема ФАЛЕСА Докажем теорему Фалеса: если на одной
- 15. Прямоугольник Прямоугольником называется параллелограмм, у которого все углы
- 16. Докажем обратное утверждение (признак прямоугольника). Если в параллелограмме
- 17. Ромб и квадрат Ромбом называется параллелограмм, у которого
- 18. Квадратом называется прямоугольник, у которого все стороны
- 19. Осевая и центральная симметрии Две точки А и
- 20. Фигура называется симметричной относительно прямой а, если
- 21. Имеются фигуры, у которых нет ни одной
- 22. Фигура называется симметричной относительно точки О, если
- 23. С симметрией мы часто встречаемся в искусстве,
- 24. Рассмотрим решение задач.
- 25. Задача. Через середину М стороны АВ треугольника ABC
- 26. Постройте параллелограмм:- по двум смежным сторонам и
- 27. Построение Строим треугольник ABD так, чтобы его стороны
- 28. Спасибо за внимание!
Слайд 2Многоугольники
Многоугольник
Выпуклый многоугольник
Четырёхугольник
Параллелограмм и трапеция
Параллелограмм
Свойства параллелограмма
Признаки параллелограмма
Трапеция
Теорема Фалеса
Прямоугольник, ромб, квадрат
Прямоугольник
Ромб и квадрат
Осевая
РАССМАТРИВАЕМЫЕ ВОПРОСЫ
Слайд 3МНОГОУГОЛЬНИК
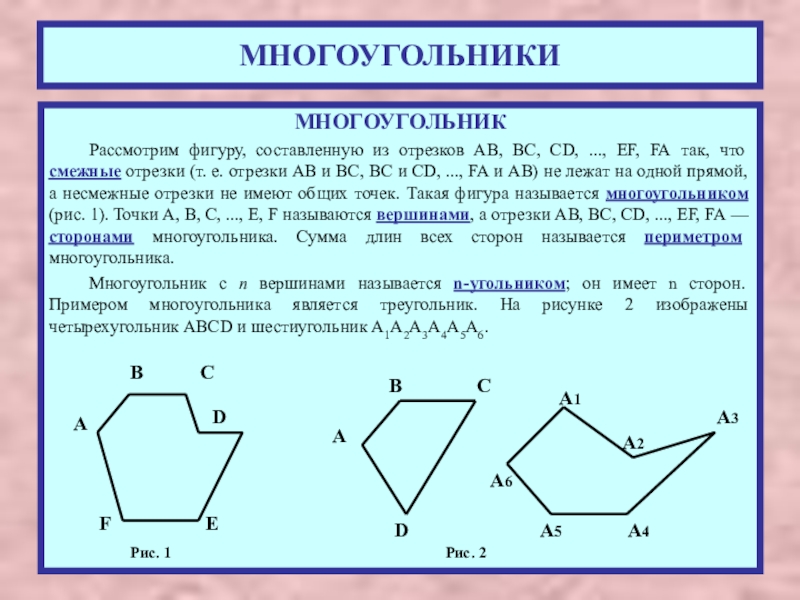
Рассмотрим фигуру, составленную из отрезков АВ, ВС, CD, ..., EF, FA
Многоугольник с п вершинами называется n-угольником; он имеет n сторон. Примером многоугольника является треугольник. На рисунке 2 изображены четырехугольник ABCD и шестиугольник A1A2A3A4A5A6.
МНОГОУГОЛЬНИКИ
А
В
С
D
E
F
Рис. 1
А
А6
А1
А2
А3
А4
А5
В
С
D
Рис. 2
Слайд 4Обрати внимание!
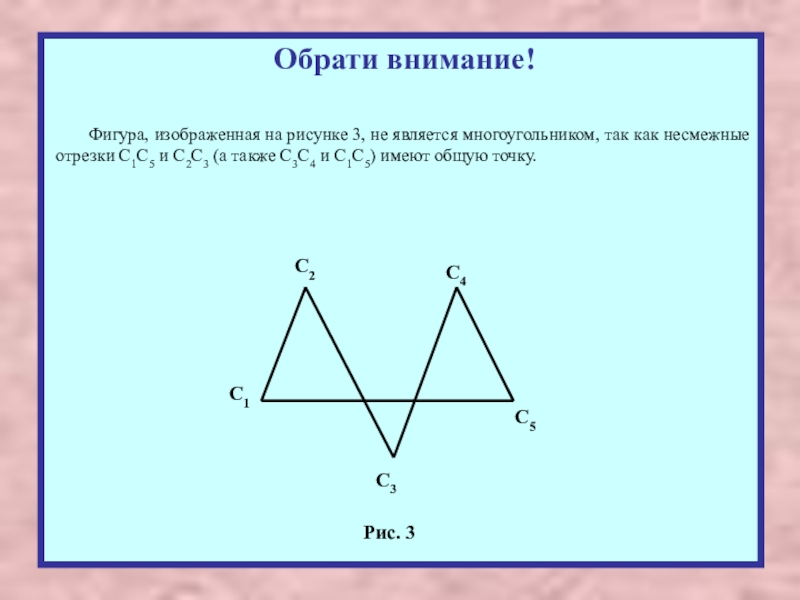
Фигура, изображенная на рисунке 3, не является многоугольником, так как
С1
С5
С4
С3
С2
Рис. 3
Слайд 5 Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая — внешней областью многоугольника.
На рисунке 4 внутренние области многоугольников закрашены. Фигуру, состоящую из сторон многоугольника и его внутренней области, также называют многоугольником.
Рис. 4
Слайд 6Выпуклый многоугольник
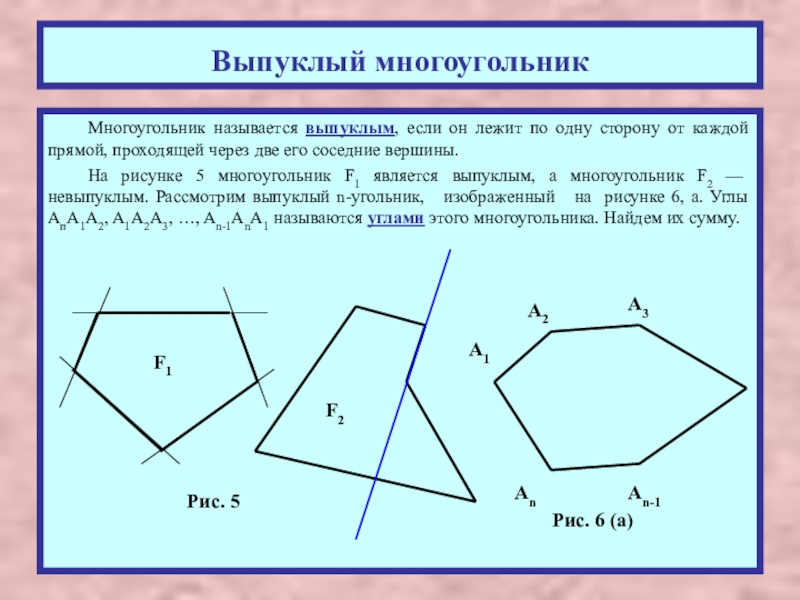
Многоугольник называется выпуклым, если он лежит по одну сторону
На рисунке 5 многоугольник F1 является выпуклым, а многоугольник F2 — невыпуклым. Рассмотрим выпуклый n-угольник, изображенный на рисунке 6, а. Углы АпА1А2, A1A2A3, …, An-1AnA1 называются углами этого многоугольника. Найдем их сумму.
F1
F2
Рис. 5
A1
An
An-1
A3
A2
Рис. 6 (a)
Слайд 7Выпуклый многоугольник
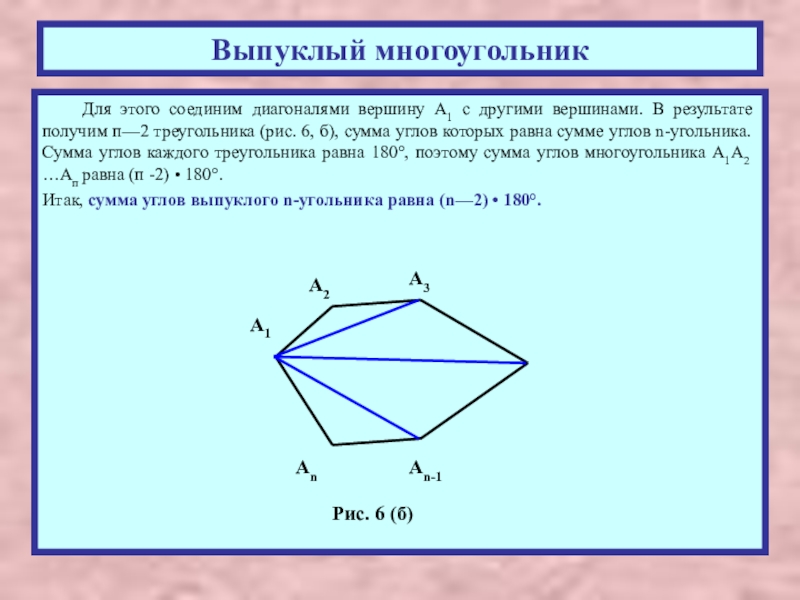
Для этого соединим диагоналями вершину А1 с другими вершинами. В
Итак, сумма углов выпуклого n-угольника равна (n—2) • 180°.
A1
An
An-1
A3
A2
Рис. 6 (б)
Слайд 8Четырёхугольник
Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали (рис.
Четырехугольники бывают выпуклые и невыпуклые. На рисунке 156, а изображен выпуклый четырехугольник, а на рисунке 7, б — невыпуклый.
Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника. Одна из диагоналей невыпуклого четырехугольника также разделяет его на два треугольника (см. рис. 7, б).
Так как сумма углов выпуклого n-угольника равна (n—2) • 180°, то сумма углов выпуклого четырехугольника равна 360°.
Рис. 7
а)
б)
A1
A2
A3
A4
A1
A2
A3
A4
Слайд 9Параллелограмм
Определение
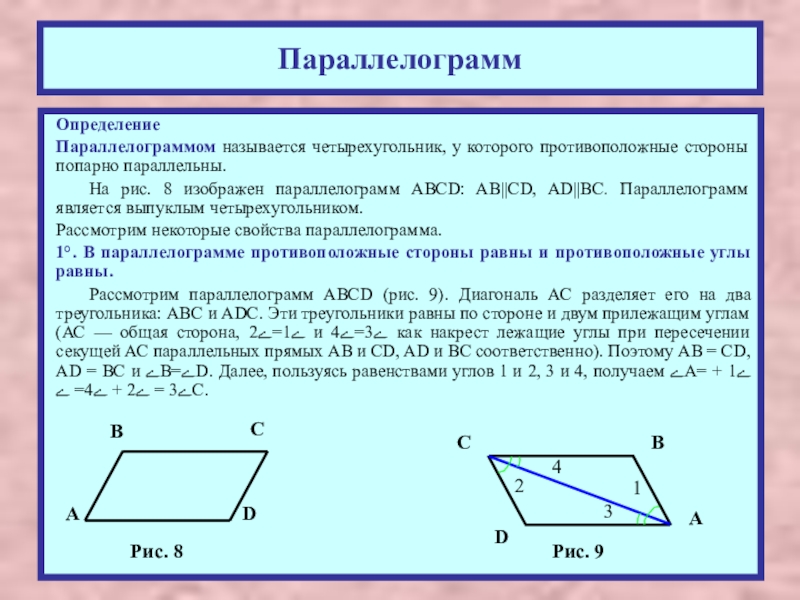
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
На рис. 8
Рассмотрим некоторые свойства параллелограмма.
1°. В параллелограмме противоположные стороны равны и противоположные углы равны.
Рассмотрим параллелограмм ABCD (рис. 9). Диагональ АС разделяет его на два треугольника: ABC и ADC. Эти треугольники равны по стороне и двум прилежащим углам (АС — общая сторона, ے1=ے2 и ے3=ے4 как накрест лежащие углы при пересечении секущей АС параллельных прямых АВ и CD, AD и ВС соответственно). Поэтому AB = CD, AD = BC и ےB=ےD. Далее, пользуясь равенствами углов 1 и 2, 3 и 4, получаем ےA= ے1 + ے3 = ے2 + ے4= ےC.
A
B
C
D
A
B
C
D
Рис. 8
Рис. 9
1
3
2
4
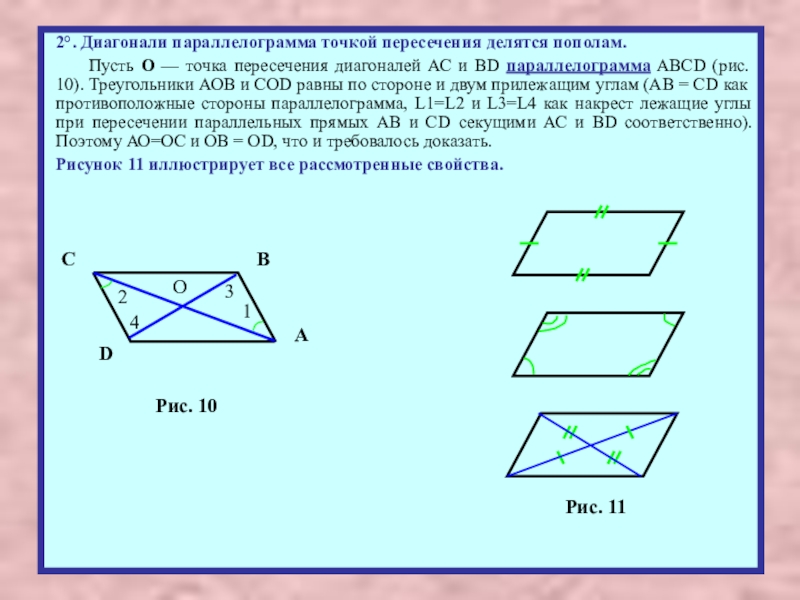
Слайд 102°. Диагонали параллелограмма точкой пересечения делятся пополам.
Пусть О — точка пересечения
Рисунок 11 иллюстрирует все рассмотренные свойства.
A
B
C
D
O
1
2
4
3
Рис. 10
Рис. 11
Слайд 11Признаки параллелограмма
Рассмотрим три признака параллелограмма.
1°. Если в четырехугольнике две стороны равны
Пусть в четырехугольнике ABCD стороны АВ и CD параллельны и AB = CD (см. рис. 12).
Проведем диагональ АС, разделяющую данный четырехугольник на два треугольника: ABC и CDA. Эти треугольники равны по двум сторонам и углу между ними (АО — общая сторона, AB=CD по условию, ے1=ے2 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущей АС), поэтому ے3=ے4. Но углы 3 и 4 накрест лежащие при пересечении прямых AD и ВС секущей АС, следовательно, AD||ВС.
Таким образом, в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD — параллелограмм.
A
B
C
D
Рис. 12
1
3
4
2
Слайд 122°. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник
Проведем диагональ АС данного четырехугольника ABCD, разделяющую его на треугольники ABC и CDA (см. рис. 13). Эти треугольники равны по трем сторонам (АС — общая сторона, AB = CD и BC=DA по условию), поэтому L1 =L2. Отсюда следует, что АВ||CD. Так как AB = CD и AB||CD, то по признаку 1° четырехугольник ABCD — параллелограмм.
3°. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Рассмотрим четырехугольник ABCD, в котором диагонали АС и BD пересекаются в точке О и делятся этой точкой пополам (см. рис. 14). Треугольники АОВ и COD равны по первому признаку равенства треугольников (АО = ОС, BO = OD по условию, ےAOB = ےCOD как вертикальные углы, поэтому АВ = CD и ےl = ے2. Из равенства углов 1 и 2 следует, что АВ || CD.
Итак, в четырехугольнике ABCD стороны АВ и CD равны и параллельны, значит, по признаку 1° четырехугольник ABCD — параллелограмм.
A
B
C
D
Рис. 13
A
B
C
D
O
1
2
4
3
Рис. 14
1
3
2
4
Слайд 13Трапеция
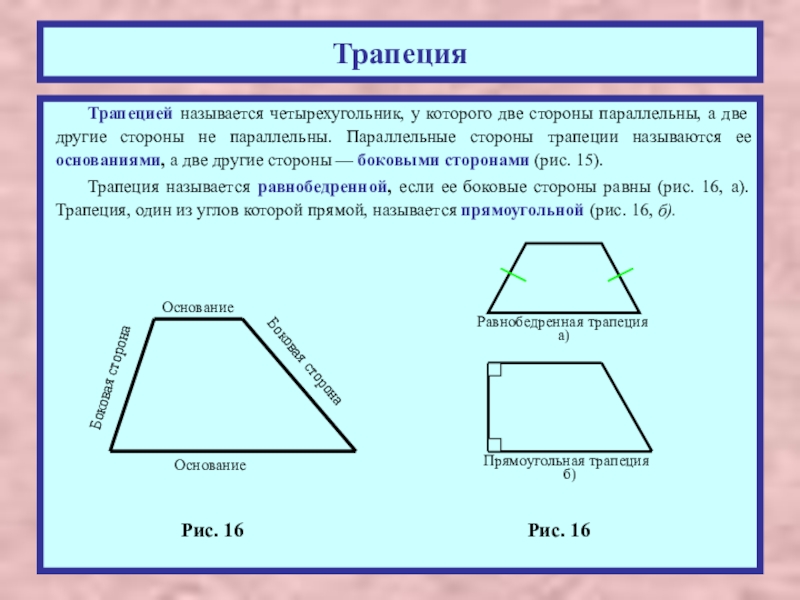
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие
Трапеция называется равнобедренной, если ее боковые стороны равны (рис. 16, а). Трапеция, один из углов которой прямой, называется прямоугольной (рис. 16, б).
Равнобедренная трапеция
а)
Прямоугольная трапеция
б)
Рис. 16
Основание
Боковая сторона
Основание
Боковая сторона
Рис. 16
Слайд 14Теорема ФАЛЕСА
Докажем теорему Фалеса: если на одной из двух прямых отложить
Решение.
Пусть на прямой L1 отложены равные отрезки A1A2, A2A3, A3A4 и через их концы проведены параллельные прямые, которые пересекают прямую L2 в точках B1, B3, B4, ... (рис. 17). Требуется доказать, что отрезки B1B2, B2B3, B3B4, … равны друг другу. Докажем, например, что B1B2=B3B4. Рассмотрим сначала случай, когда прямые L1 и L2 параллельны (рис. 17, а). Тогда А1А2=В1В2 и А2A3=B2B3 как противоположные стороны параллелограммов A1B1B2A2 и A2B2B3A3. Так как A1A2=A2A3, то и B1B2=B2B3. Если прямые L1 и L2 не параллельны, то через точку B1 проведем прямую L, параллельную прямой L1 (рис. 17, б). Она пересечет прямые А2В2 и A3B3 в некоторых точках С и D. Так как А1А2=А2А3, то по доказанному B1C=CD. Отсюда получаем В1В2=В2В3 (задача 1). Аналогично можно доказать, что B2B3=B3B4 и т. д.
Рис. 17
Слайд 15Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Так как прямоугольник является
Рассмотрим особое свойство прямоугольника.
Диагонали прямоугольника равны.
Действительно, обратимся к рисунку 18, на котором изображен прямоугольник ABCD с диагоналями АС и BD. Прямоугольные треугольники ACD и DBA равны по двум катетам (CD=BA, AD — общий катет). Отсюда следует, что гипотенузы этих треугольников равны, т.е. AC = BD, что и требовалось доказать.
A
B
C
D
Рис. 18
Слайд 16Докажем обратное утверждение (признак прямоугольника).
Если в параллелограмме диагонали равны, то этот
Пусть в параллелограмме ABCD диагонали АС и BD равны (см. рис. 19). Треугольники ABD и DCA равны по трем сторонам (AB=DC, BD=CA, AD— общая сторона). Отсюда следует, что ےA= ےD. Так как в параллелограмме противоположные углы равны, то LA=LC и LB=LD. Таким образом, ے A= ے B= ے C= ے D. Параллелограмм — выпуклый четырехугольник, поэтому ےA+ ےB+ ےC+ ےD=360°. Следовательно, ےA= ےB= ےC= ےD = 90°, т.е. параллелограмм ABCD является прямоугольником.
A
B
C
D
Рис. 19
Слайд 17Ромб и квадрат
Ромбом называется параллелограмм, у которого все стороны равны. Так
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Рассмотрим ромб ABCD (рис. 20). Требуется доказать, что AC┴BD и каждая диагональ делит соответствующие углы ромба пополам. Докажем, например, что ےBAC=ےDAC.
По определению ромба AB=AD, поэтому треугольник BAD равнобедренный. Так как ромб — параллелограмм, то его диагонали точкой О пересечения делятся пополам. Следовательно, АО — медиана равнобедренного треугольника BAD, а значит, высота и биссектриса этого треугольника. Поэтому AC┴BD и ےBAC=ےDAC, что и требовалось доказать.
A
B
C
D
O
Рис. 20
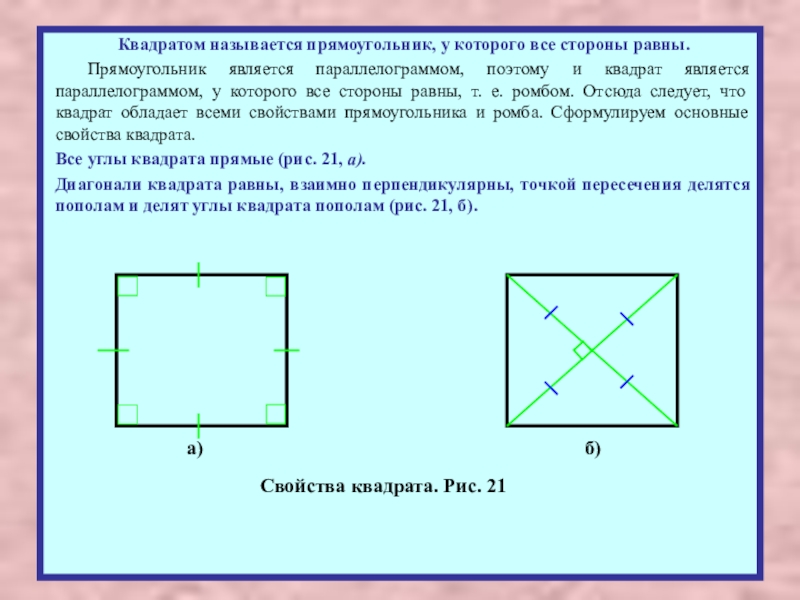
Слайд 18Квадратом называется прямоугольник, у которого все стороны равны.
Прямоугольник является параллелограммом, поэтому
Все углы квадрата прямые (рис. 21, а).
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам (рис. 21, б).
а)
б)
Свойства квадрата. Рис. 21
Слайд 19Осевая и центральная симметрии
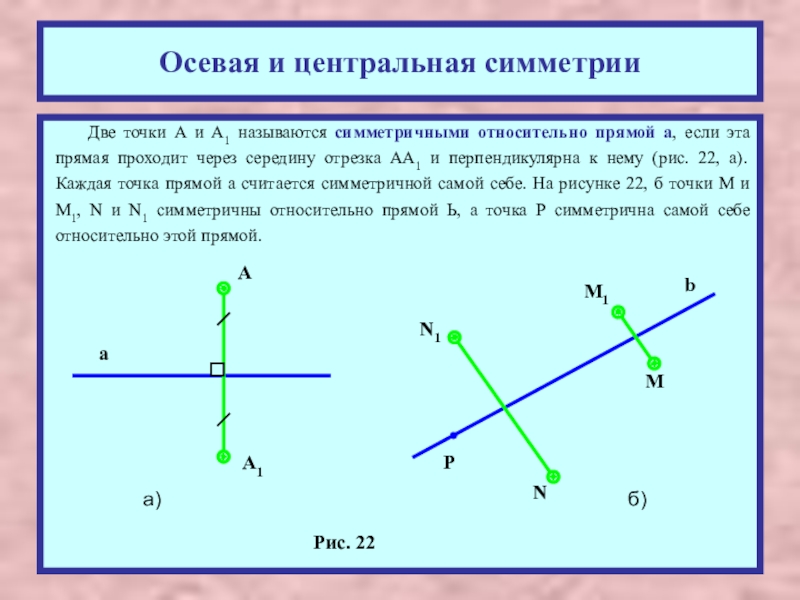
Две точки А и А1 называются симметричными относительно
а
А1
А
Р
N
N1
M
M1
b
Рис. 22
а)
б)
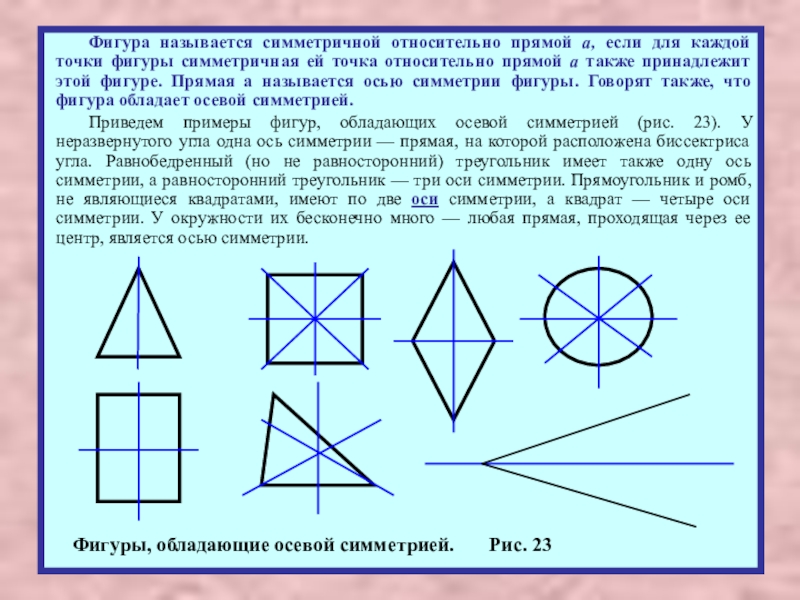
Слайд 20 Фигура называется симметричной относительно прямой а, если для каждой точки фигуры
Приведем примеры фигур, обладающих осевой симметрией (рис. 23). У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла. Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник — три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат — четыре оси симметрии. У окружности их бесконечно много — любая прямая, проходящая через ее центр, является осью симметрии.
Фигуры, обладающие осевой симметрией. Рис. 23
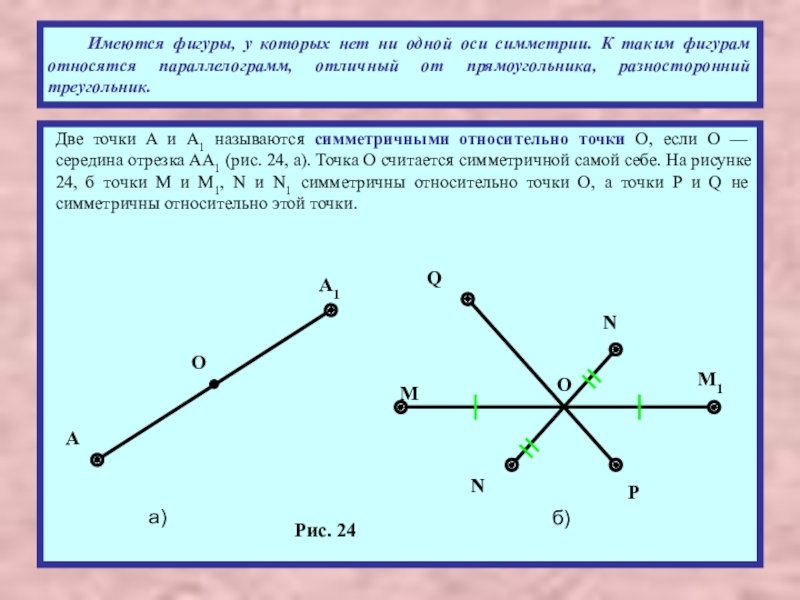
Слайд 21 Имеются фигуры, у которых нет ни одной оси симметрии. К таким
Две точки A и А1 называются симметричными относительно точки О, если О — середина отрезка АА1 (рис. 24, а). Точка О считается симметричной самой себе. На рисунке 24, б точки М и M1, N и N1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.
А
А1
О
P
М1
М
Q
N
N
O
Рис. 24
а)
б)
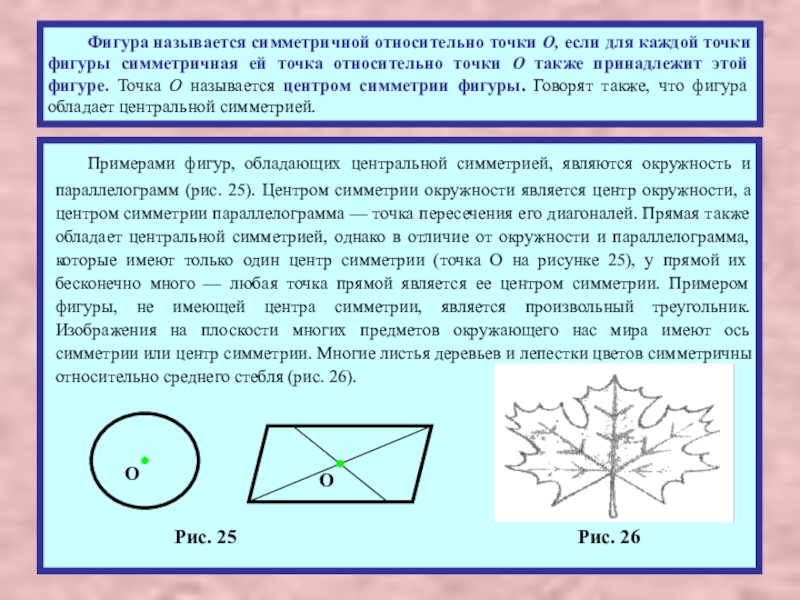
Слайд 22 Фигура называется симметричной относительно точки О, если для каждой точки фигуры
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм (рис. 25). Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии (точка О на рисунке 25), у прямой их бесконечно много — любая точка прямой является ее центром симметрии. Примером фигуры, не имеющей центра симметрии, является произвольный треугольник. Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля (рис. 26).
O
O
Рис. 25
Рис. 26
Слайд 23
С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Так,
Рис. 27
Слайд 25Задача.
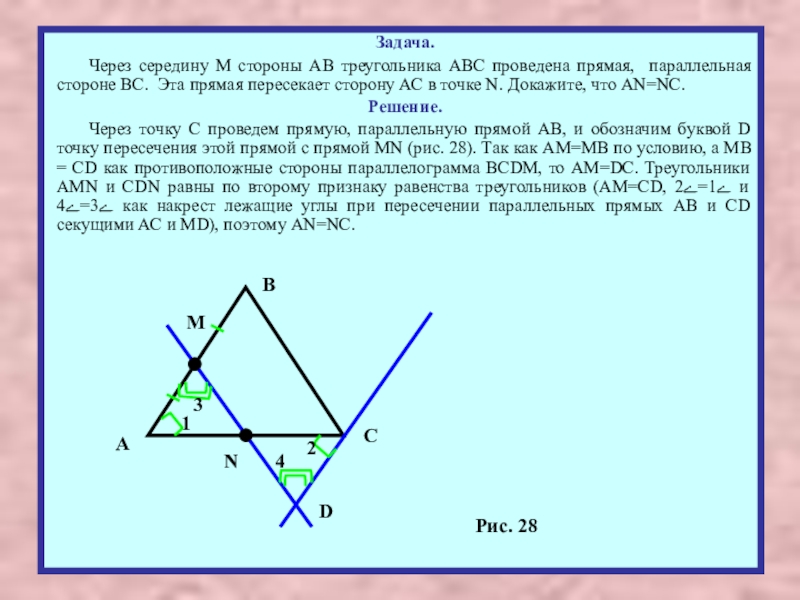
Через середину М стороны АВ треугольника ABC проведена прямая, параллельная стороне
Решение.
Через точку С проведем прямую, параллельную прямой АВ, и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 28). Так как АМ=МВ по условию, a MB = CD как противоположные стороны параллелограмма BCDM, то AM=DC. Треугольники AMN и CDN равны по второму признаку равенства треугольников (AM=CD, ے1=ے2 и ے3=ے4 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущими АС и MD), поэтому AN=NC.
A
M
B
N
D
C
1
3
2
4
Рис. 28
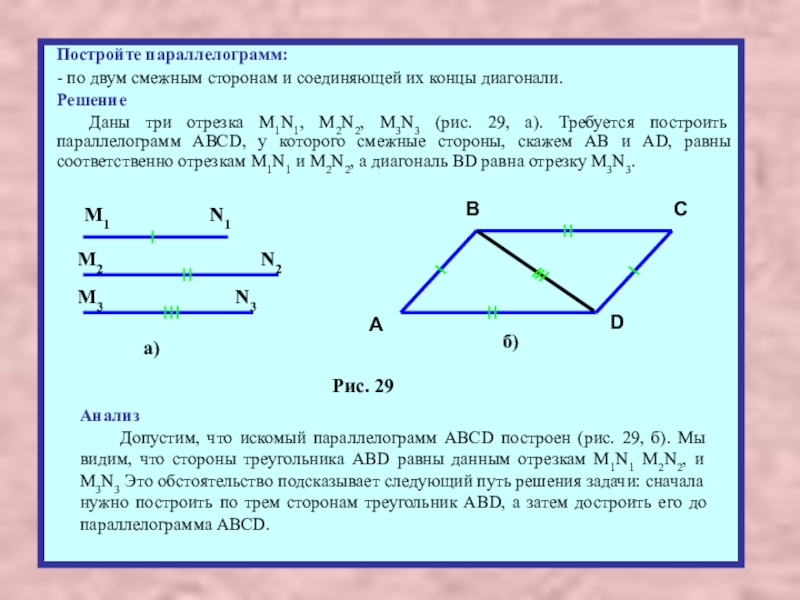
Слайд 26Постройте параллелограмм:
- по двум смежным сторонам и соединяющей их концы диагонали.
Решение
Даны
M1
N1
M2
N2
M3
N3
Анализ
Допустим, что искомый параллелограмм ABCD построен (рис. 29, б). Мы видим, что стороны треугольника ABD равны данным отрезкам M1N1 M2N2, и M3N3 Это обстоятельство подсказывает следующий путь решения задачи: сначала нужно построить по трем сторонам треугольник ABD, а затем достроить его до параллелограмма ABCD.
A
B
C
D
а)
б)
Рис. 29
Слайд 27Построение
Строим треугольник ABD так, чтобы его стороны АВ, AD и BD
Доказательство.
По построению AB||CD и BC||AD, поэтому ABCD — параллелограмм. Смежные стороны параллелограмма ABCD по построению равны отрезкам M1N1 и M2N2, а диагональ BD равна отрезку М3N3, т. е. параллелограмм ABCD — искомый.
Исследование
Ясно, что если по трем данным отрезкам M1N1, M2N2 и М3N3 можно построить треугольник ABD, стороны которого равны этим отрезкам, то можно построить и параллелограмм ABCD. Но треугольник ABD можно построить не всегда. Если какой-то из трех данных отрезков больше или равен сумме двух других, то треугольник ABD, а значит , и параллелограмм ABCD построить нельзя.
A
B
C
D
в) Рис. 29