- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Аксиомы стереометрии.
Содержание
- 1. Аксиомы стереометрии.
- 2. Аксиомы стереометрии.
- 3. Аксиома 1(С1): Какова бы ни
- 4. Аксиома 2(С2): Если две различные
- 5. Аксиома 3(С3): Если две различные
- 6. Аксиомы планиметрии.
- 7. Аксиома I: Какова бы не
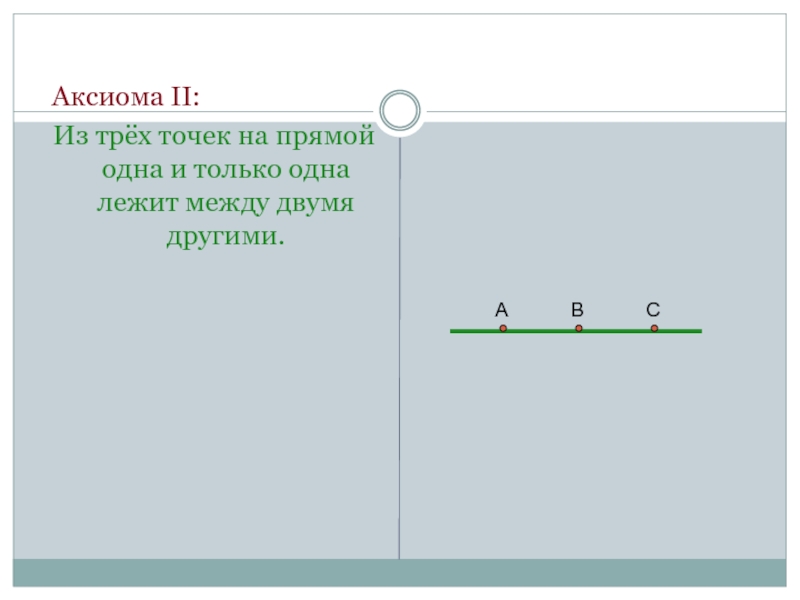
- 8. Аксиома II:Из трёх точек на прямой одна и только одна лежит между двумя другими.АВС
- 9. Аксиома III: Каждый отрезок имеет
- 10. Аксиома III: Каждый отрезок имеет
- 11. Аксиома III: Каждый отрезок имеет
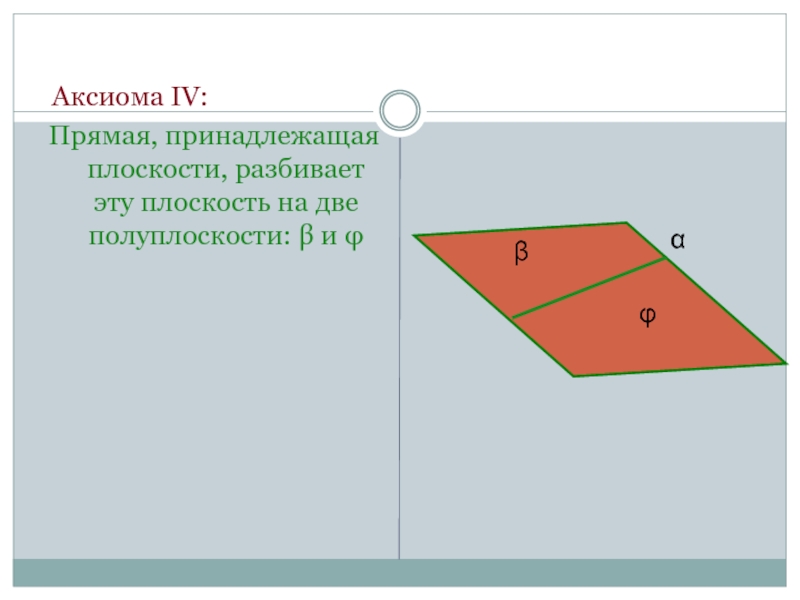
- 12. Аксиома IV:Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости: β и φβαφ
- 13. Аксиома V:Каждый угол имеет определённую градусную
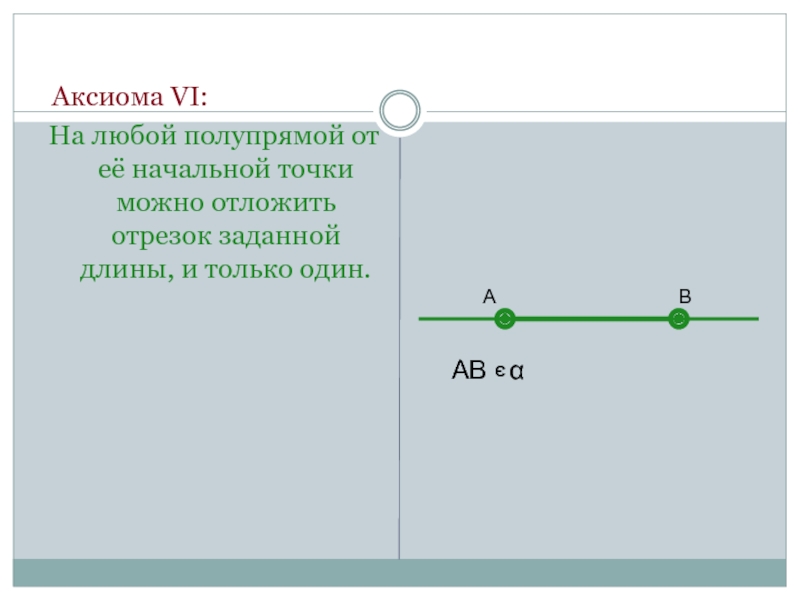
- 14. Аксиома VI:На любой полупрямой от её
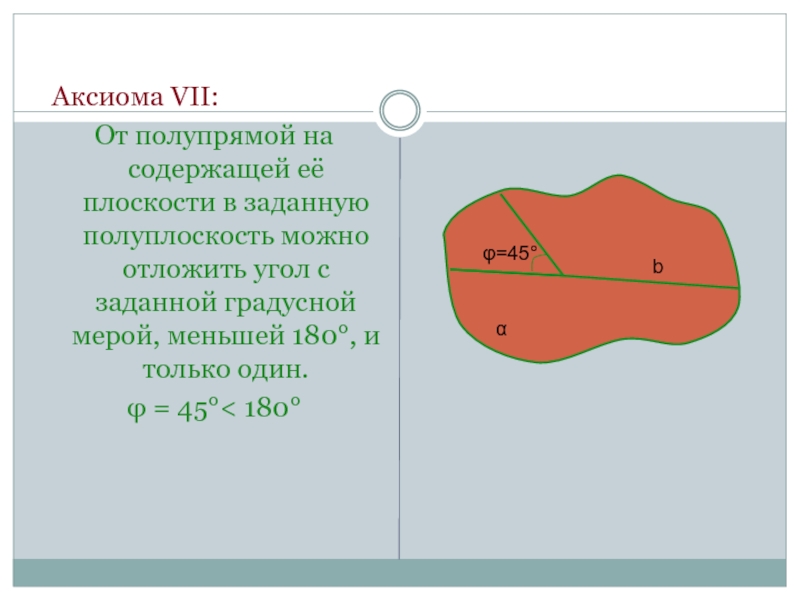
- 15. Аксиома VII:От полупрямой на содержащей её
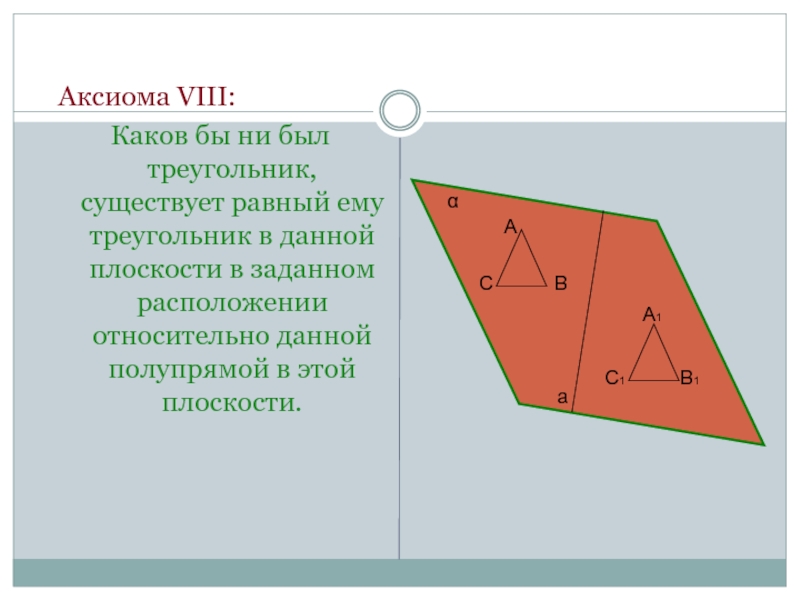
- 16. Аксиома VIII:Каков бы ни был треугольник,
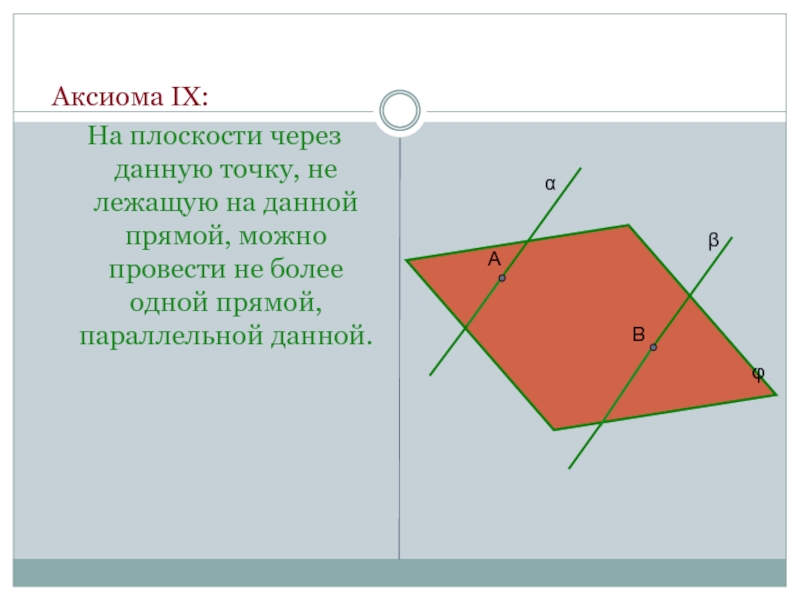
- 17. Аксиома IX:На плоскости через данную точку,
- 18. Аксиома 1(С1): Какова бы ни
- 19. Аксиома 2(С2):Если две различные плоскости имеют
- 20. Аксиома 3(С3): Если две различные прямые
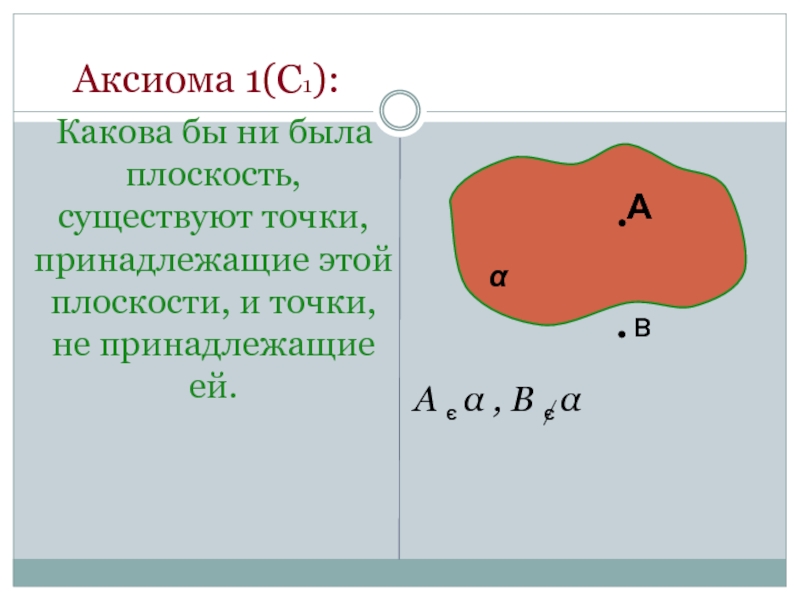
Слайд 3 Аксиома 1(С1):
Какова бы ни была плоскость, существуют точки,
А α , В α
α
Α
Э
Э
α
Α
в
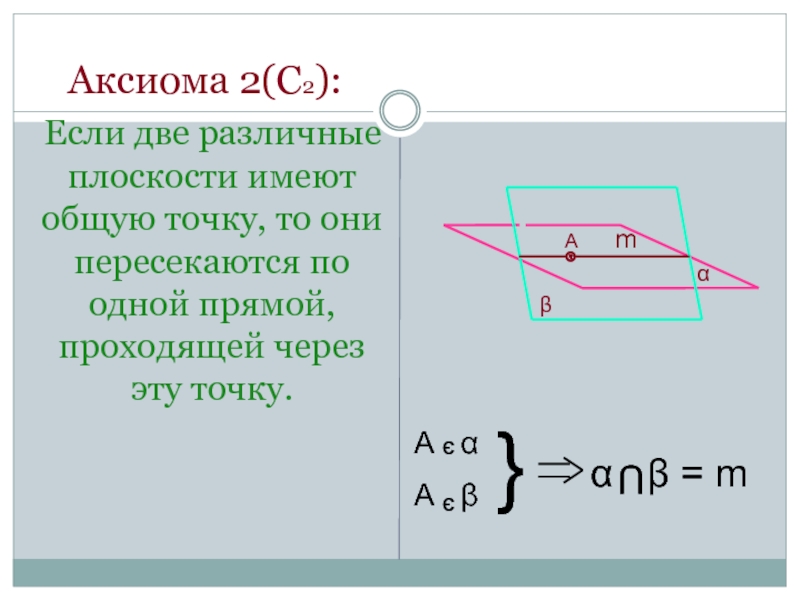
Слайд 4 Аксиома 2(С2):
Если две различные плоскости имеют общую точку,
β
α
А α
А β
Э
Э
}
α β = m
U
m
А
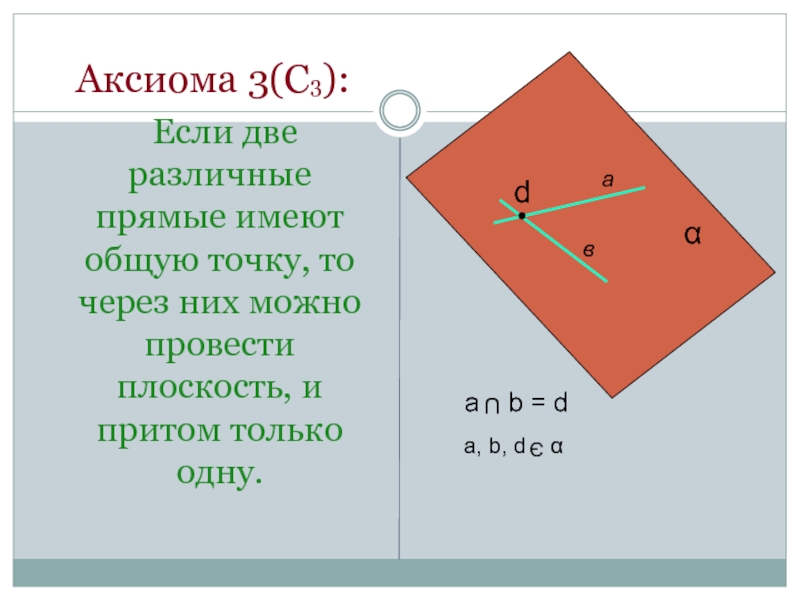
Слайд 5 Аксиома 3(С3):
Если две различные прямые имеют общую точку,
a b = d
a, b, d α
U
Э
d
α
в
a
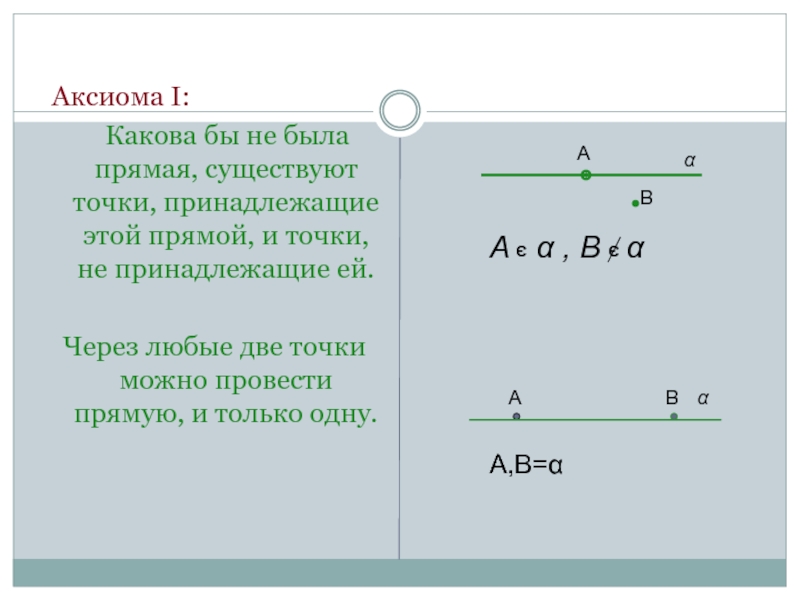
Слайд 7 Аксиома I:
Какова бы не была прямая, существуют точки,
Через любые две точки можно провести прямую, и только одну.
А α , В α
Э
Э
А
В
А,В=α
α
α
А
В
Слайд 9 Аксиома III:
Каждый отрезок имеет определённую длину, большую нуля.
А
В
АВ > 0
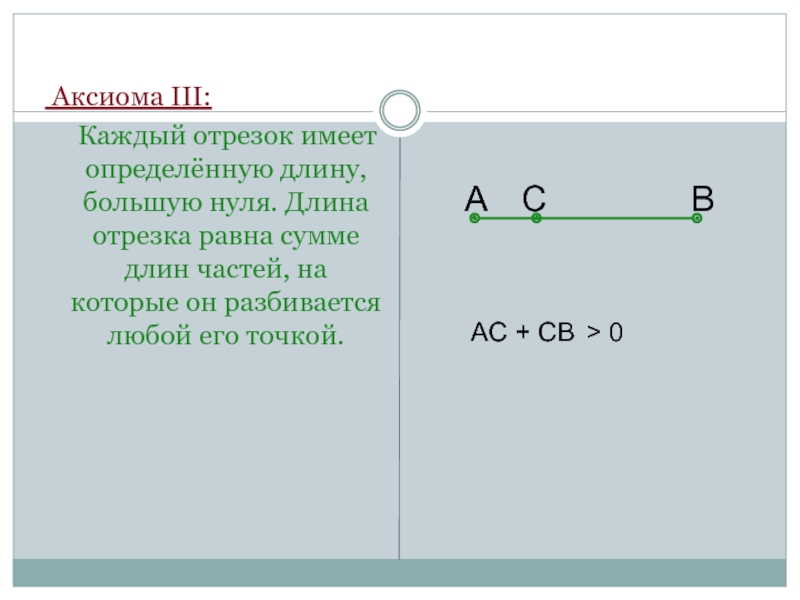
Слайд 10 Аксиома III:
Каждый отрезок имеет определённую длину, большую нуля.
А
В
АC + CВ > 0
C
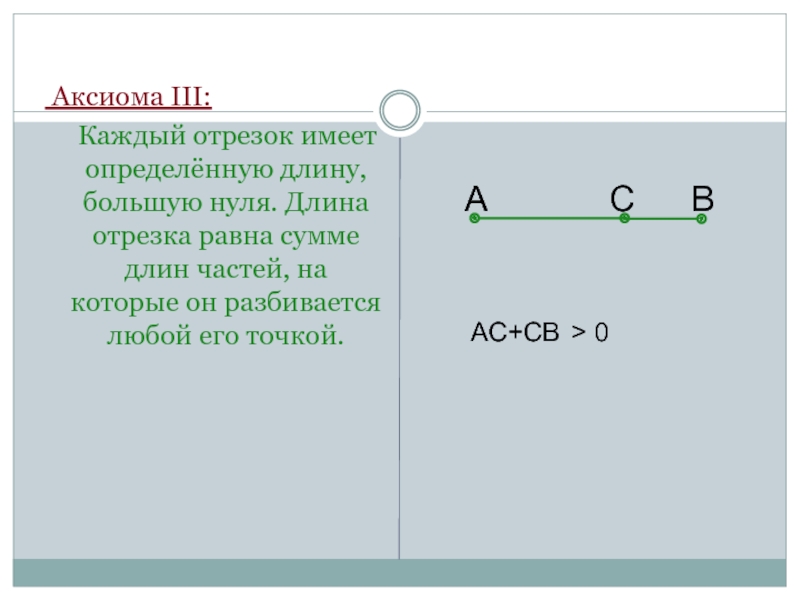
Слайд 11 Аксиома III:
Каждый отрезок имеет определённую длину, большую нуля.
А
В
АC+CВ > 0
C
Слайд 12 Аксиома IV:
Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости:
β
α
φ
Слайд 13 Аксиома V:
Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый
180
В
А
Слайд 14 Аксиома VI:
На любой полупрямой от её начальной точки можно отложить
А
В
АВ α
Э
Слайд 15 Аксиома VII:
От полупрямой на содержащей её плоскости в заданную полуплоскость
φ = 45°< 180°
α
b
φ=45°
Слайд 16 Аксиома VIII:
Каков бы ни был треугольник, существует равный ему треугольник
α
а
А
В
С
А1
В1
С1
Слайд 17 Аксиома IX:
На плоскости через данную точку, не лежащую на данной
А
α
β
φ
B
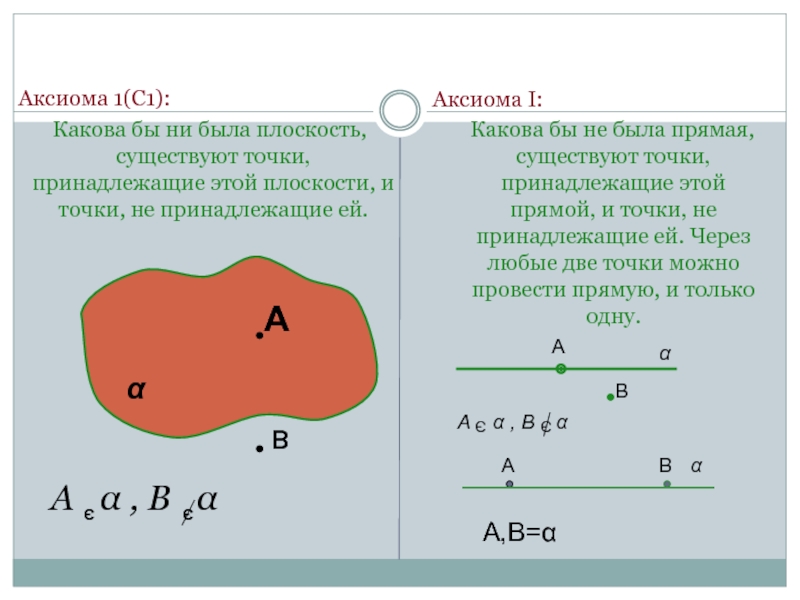
Слайд 18 Аксиома 1(С1):
Какова бы ни была плоскость, существуют точки,
А α , В α
α
Α
в
Э
Э
Аксиома I:
Какова бы не была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
α
А
В
А α , В α
Э
Э
А
В
А,В=α
α
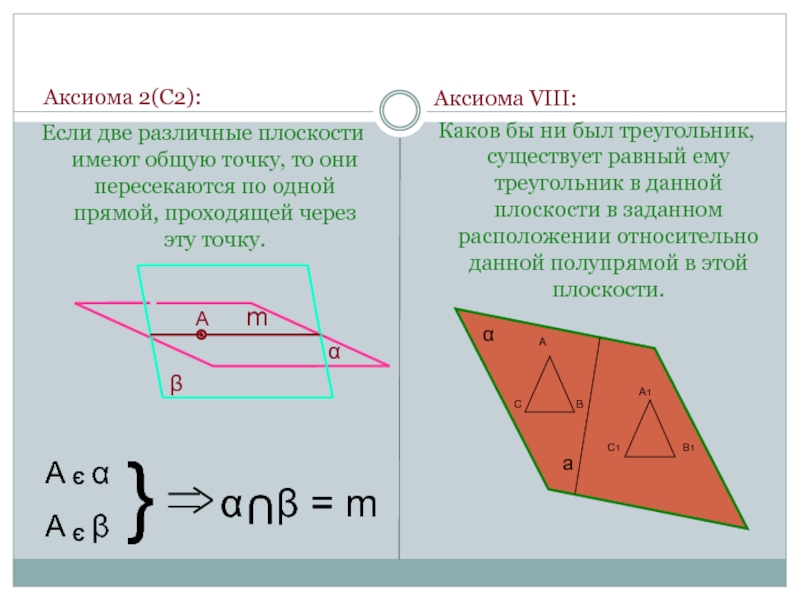
Слайд 19 Аксиома 2(С2):
Если две различные плоскости имеют общую точку, то они
β
α
Э
Э
}
α β = m
U
m
А
А α
А β
Аксиома VIII:
Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
α
а
А
В
С
А1
В1
С1
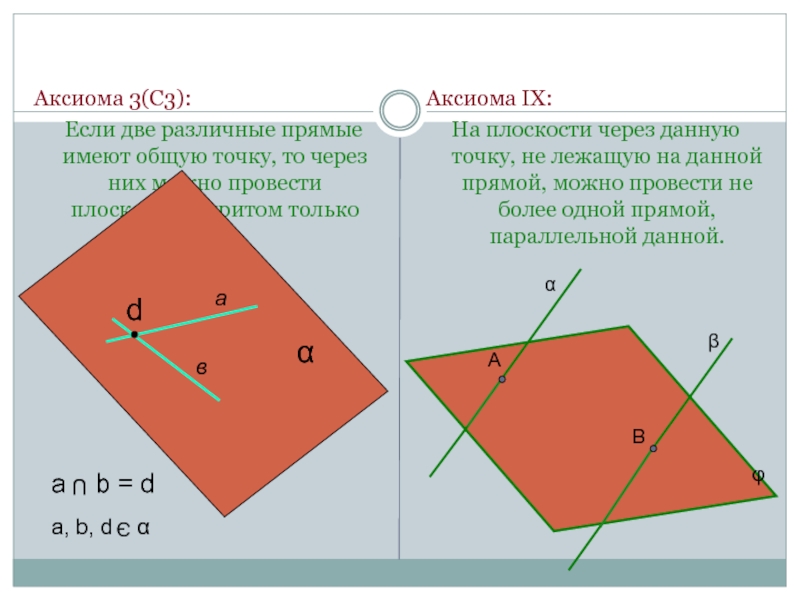
Слайд 20Аксиома 3(С3):
Если две различные прямые имеют общую точку, то
Аксиома IX:
На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
a b = d
a, b, d α
U
Э
d
α
в
a
А
α
β
φ
B