- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Аксиомы планиметрии. Презентация по геометрии для 7-9 классов.
Содержание
- 1. Аксиомы планиметрии. Презентация по геометрии для 7-9 классов.
- 2. Геометрия ЕвклидаПервым систематическим изложением геометрии, дошедшим до
- 3. В “Началах” был развит
- 4. Аксиомы планиметрии
- 5. Аксиомами называются те основные положения геометрии,
- 6. Основные понятия (фигуры) на плоскости:
- 7. Аксиомы взаимного расположения точек и прямых:1.Каждой прямой
- 8. АВПрямые и отрезкиЧерез любые две точки можно провести прямую, и притом только одну а
- 9. Аксиомы расположения точек на прямой:4. Из трёх
- 10. Аксиома расположения точек на плоскости:6. Каждая прямая
- 11. Аксиомы наложения или равенства фигур.Наложение – это
- 12. Аксиомы наложения или равенства фигур:7. Если при
- 13. Аксиомы наложения или равенства фигур:10. Любой угол
- 14. Аксиомы наложения или равенства фигур:12.
- 15. Аксиомы измерения отрезков:14. При выбранной единице измерения
- 16. Аксиома параллельных прямых:16. Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной.
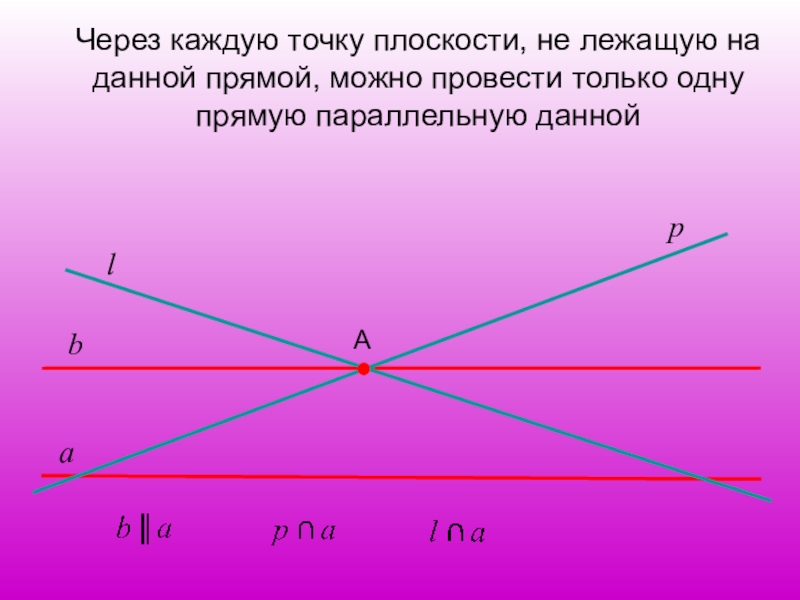
- 17. Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую параллельную даннойаАbpl
- 18. Постулаты Евклида1. Из каждой точки ко всякой
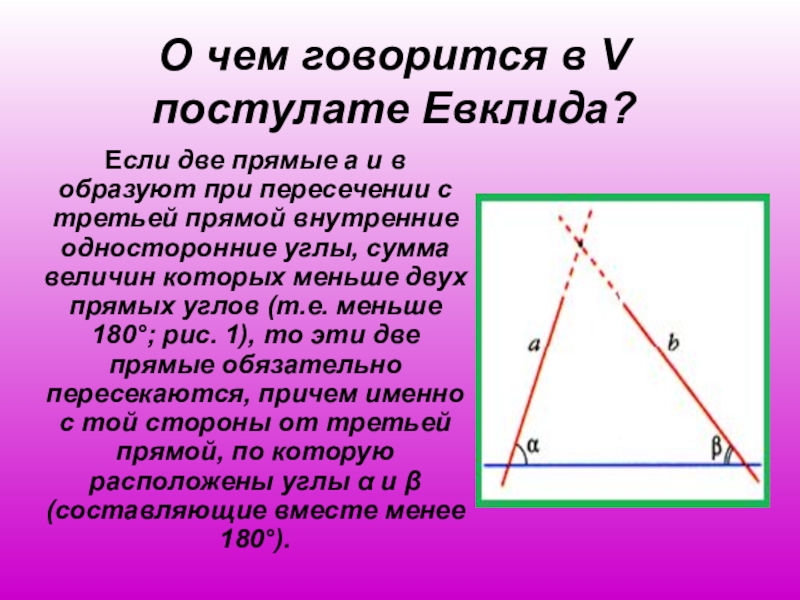
- 19. О чем говорится в V постулате Евклида?Если
Слайд 1Презентация по геометрии учителя математики МКОУ СОШ №1 Розовой С М пгт. Палана Камчатский край Учебник геометрии
Слайд 2Геометрия Евклида
Первым систематическим изложением геометрии, дошедшим до нашего времени, являются “Начала”
Слайд 3 В “Началах” был развит аксиоматический подход к построению
Изложение геометрии Евклидом долгое время служило недосягаемым образцом точности, безукоризненности и строгости.
Только в начале 20 века математики смогли улучшить логические основания геометрии.
«Начала»
Слайд 5 Аксиомами называются те основные положения геометрии, которые принимаются в качестве
Или :
Аксиомами называются утверждения, которые принимаются без доказательства.
Слайд 6Основные понятия (фигуры) на плоскости:
Используя основные понятия и аксиомы даются определения новых понятий, формулируются и доказываются теоремы о свойствах геометрических фигур.
Слайд 7Аксиомы взаимного расположения точек и прямых:
1.Каждой прямой принадлежит по крайней мере
2. Имеются по крайней мере три точки, не лежащие на одной прямой.
3. Через любые две точки проходит прямая, и притом только одна.
Слайд 9Аксиомы расположения точек на прямой:
4. Из трёх точек прямой одна и
5. Каждая точка О прямой разделяет её на две части(два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
Слайд 10
Аксиома расположения точек на плоскости:
6. Каждая прямая а разделяет плоскость на
Слайд 11Аксиомы наложения или равенства фигур.
Наложение – это отображение плоскости на себя.
Если
Слайд 12Аксиомы наложения или равенства фигур:
7. Если при наложении совмещаются концы двух
Слайд 13
Аксиомы наложения или равенства фигур:
10. Любой угол hk можно совместить наложением
Слайд 14
Аксиомы наложения или равенства фигур:
12. Если фигура Ф равна
13. Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.
Слайд 15Аксиомы измерения отрезков:
14. При выбранной единице измерения отрезков длина каждого отрезка
Аксиома существования отрезка данной длины:
15. При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.
Слайд 16Аксиома параллельных прямых:
16. Через точку, не лежащую на данной прямой, проходит
Слайд 17Через каждую точку плоскости, не лежащую на данной прямой, можно провести
а
А
b
p
l
Слайд 18Постулаты Евклида
1. Из каждой точки ко всякой другой точке можно провести
2. Каждую ограниченную прямую можно продолжить неопределённо;
3. Из любого центра можно описать окружность любого радиуса;
4. Все прямые углы равны;
5. И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньше двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых