- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему 8 сыйныф өчен геометриядән дәрес эшкәртмәсе
Содержание
- 1. 8 сыйныф өчен геометриядән дәрес эшкәртмәсе
- 2. КерешУкучының
- 3. Инструменлар наборы
- 4. Инструменлар наборы
- 5. Слайд 5
- 6. Геометриядә төзүгә мәсьәләләрне арып
- 7. Гадәттә, циркуль һәм линейка ярдәмендә төзүгә мәсьәләләрне
- 8. АВСБирелгән помак буенча почмак төзүБирелгән: АБирелгән
- 9. Построение угла, равного данному.Бирелгән: ААО почмагын
- 10. биссектрисаПочмакның биссектрисасын төзү. КҮРСӘТЕРГӘ
- 11. АВ нуры – А посмагының биссектрисасы икәнен
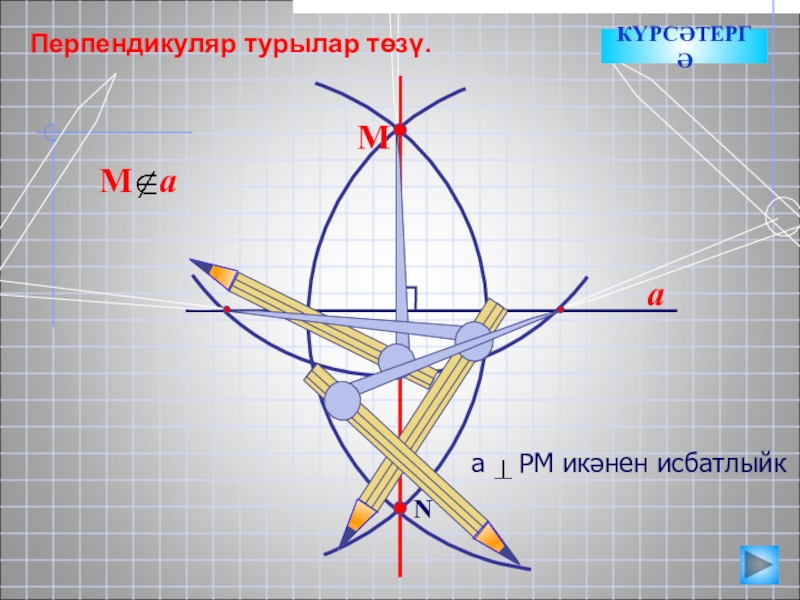
- 12. ВАКҮРСӘТЕРГӘПерпендикуляр турылартөзү.
- 13. МaАМ=МВ, бер әйләнәнең радиуслары буларак.АР=РВ, бер әйләнәнең
- 14. aNМПерпендикуляр турылар төзү. КҮРСӘТЕРГӘ
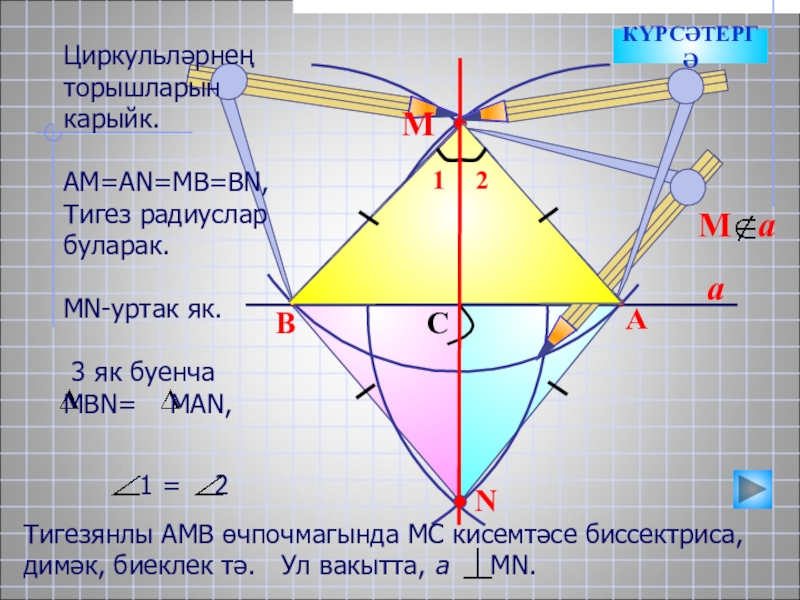
- 15. aNBACМКҮРСӘТЕРГӘЦиркульләрнең торышларын карыйк.АМ=АN=MB=BN, Тигез радиуслар буларак. МN-уртак
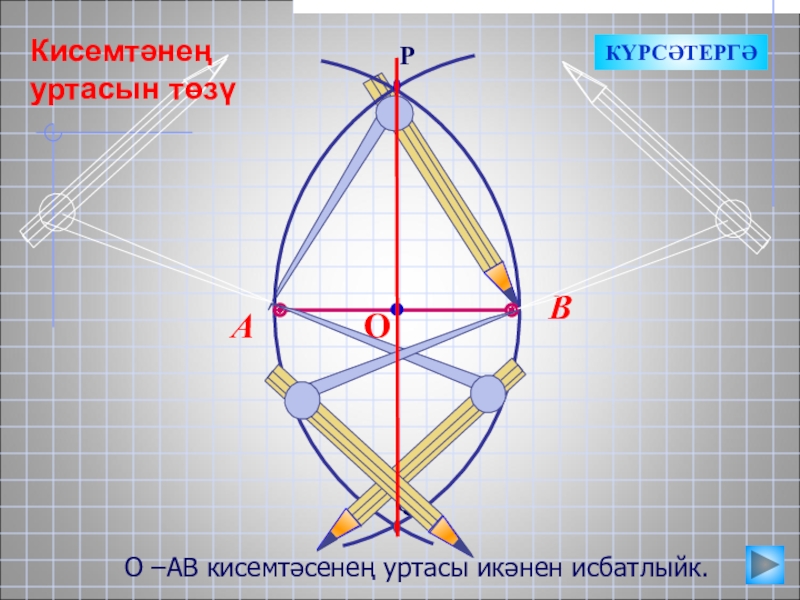
- 16. О –АВ кисемтәсенең уртасы икәнен исбатлыйк.КҮРСӘТЕРГӘКисемтәнең уртасын төзү
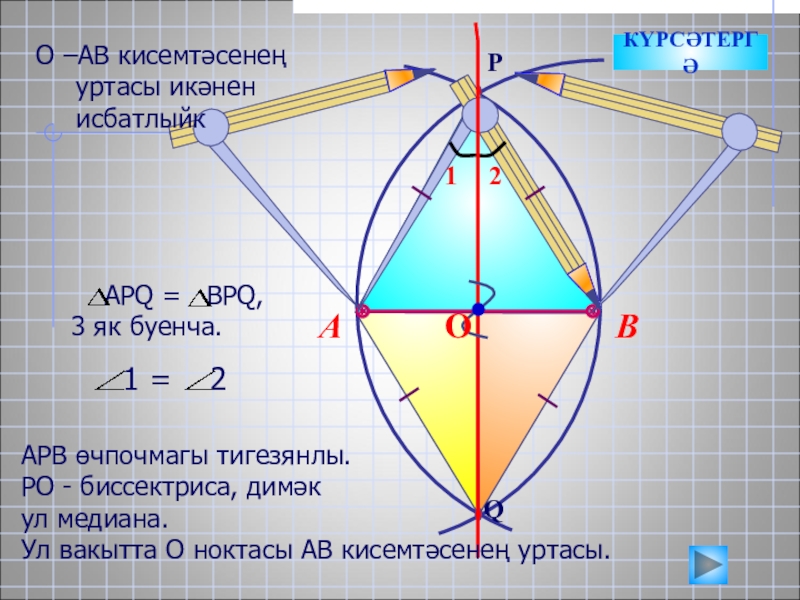
- 17. ВААРВ өчпочмагы тигезянлы.РО - биссектриса, димәкул медиана.
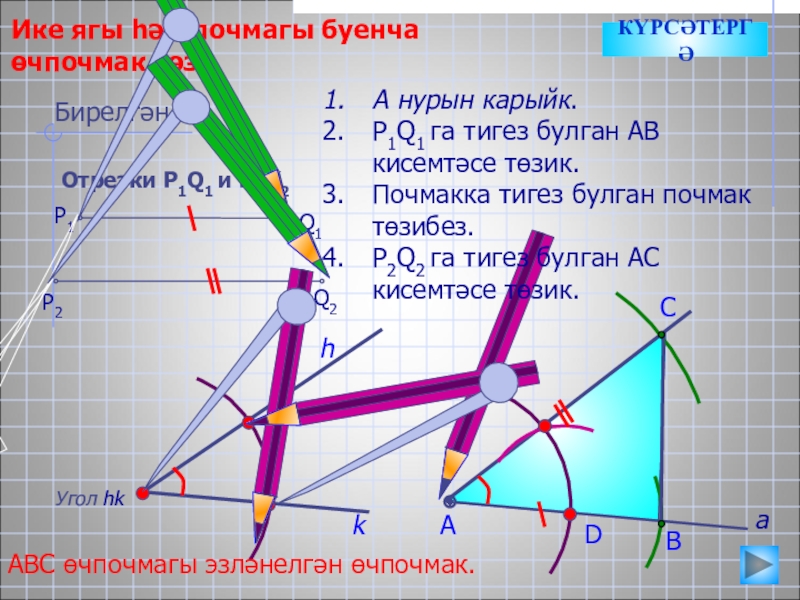
- 18. DСИке ягы һәм почмагы буенча өчпочмак төзү.
- 19. 1 нче вариант№395397 (а)2 нче вариант№395397 (а)
- 20. Өй эше№396, 393(в) мәсьәләләрнең чишелешен укып килергә;№394, 398.
- 21. DСПостроение треугольника по стороне и двум прилежащим
- 22. СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим
- 23. Методы решения задач на
- 24. НЕРАЗРЕШИМЫЕ
- 25. НЕРАЗРЕШИМЫЕ НЕРАЗРЕШИМЫЕ
- 26. НЕРАЗРЕШИМЫЕ
КерешУкучының һәм инженерның геометрик инструменты 1.Линейка. 2.Циркуль. 3.Транспортир.
Слайд 6 Геометриядә төзүгә мәсьәләләрне арып йөртәләр, аларны бары ике
инструмент белән чишеп була. Бу циркуль һәм масштаблы сызыклары булмаган линейка.
Линейка ярдәмендә төрле туры һәм ике нокта аша үтүче туры үткәреп була;
ә циркуль ярдәмендә төрле радиуслы өйләнә һәм шулай ук билгеле кисемтәгә тигез булган радиуслы үзәге шушы ноктага туры килгән әйләнә төзеп була.
Линейка ярдәмендә төрле туры һәм ике нокта аша үтүче туры үткәреп була;
ә циркуль ярдәмендә төрле радиуслы өйләнә һәм шулай ук билгеле кисемтәгә тигез булган радиуслы үзәге шушы ноктага туры килгән әйләнә төзеп була.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
Слайд 7Гадәттә, циркуль һәм линейка ярдәмендә төзүгә мәсьәләләрне түбәндәге схема буенча чишәләр.
1.Анализ
(мәсьәләнең эзләнелә торган элементлары белән бирелгәннәр арасында бәйләнеш булдырып, мәсьәләне чишү ысулын эзләү).
2.Билгеләнгән план буенча төзү эшләрен башкару.
3.Төзелгән фигура мәсьәләнең шартын канәгатьләндергәнен исбатлау.
4. Мәсьәләне тикшерү, ягъни теләсә нинди бирелгәннәр өчен мәсьәләнең чишелеше булу-булмавын һәм әгәр булса, ничә чишелеше булуын ачыклау.
2.Билгеләнгән план буенча төзү эшләрен башкару.
3.Төзелгән фигура мәсьәләнең шартын канәгатьләндергәнен исбатлау.
4. Мәсьәләне тикшерү, ягъни теләсә нинди бирелгәннәр өчен мәсьәләнең чишелеше булу-булмавын һәм әгәр булса, ничә чишелеше булуын ачыклау.
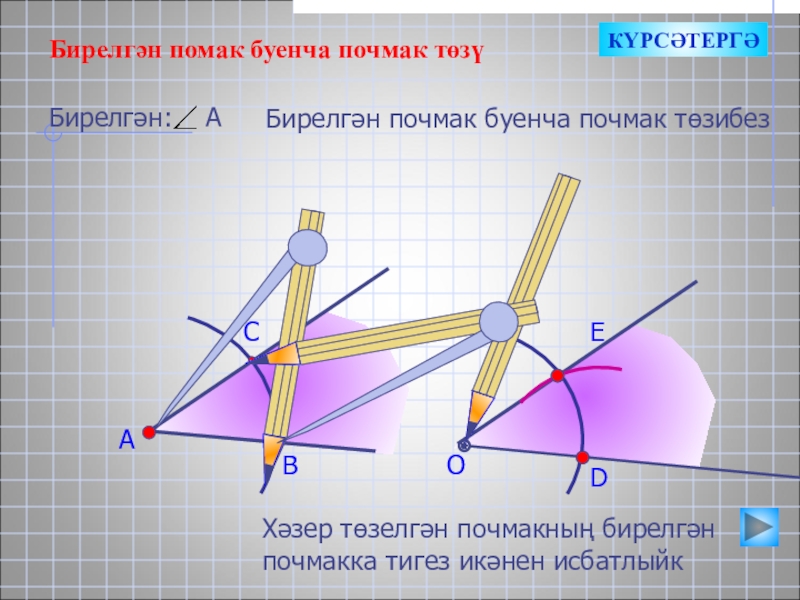
Слайд 8А
В
С
Бирелгән помак буенча почмак төзү
Бирелгән: А
Бирелгән почмак буенча почмак төзибез
О
D
E
Хәзер
төзелгән почмакның бирелгән почмакка тигез икәнен исбатлыйк
КҮРСӘТЕРГӘ
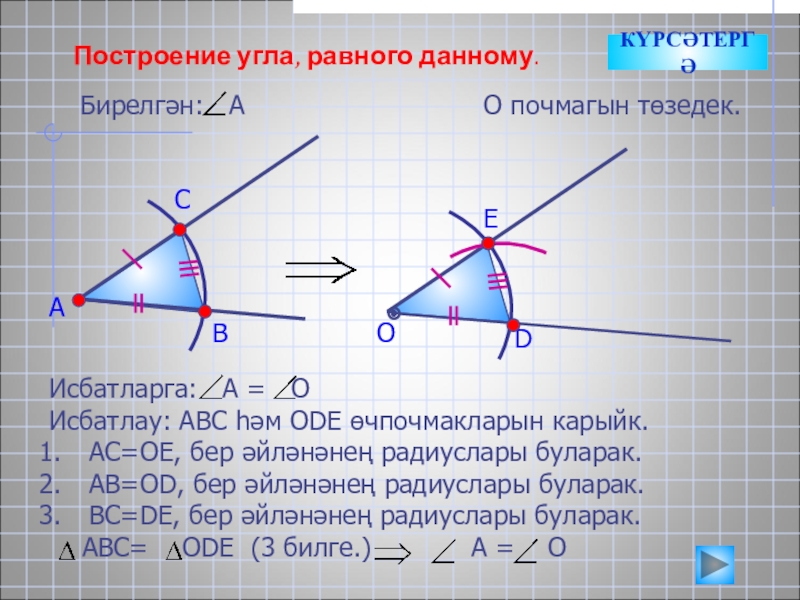
Слайд 9
Построение угла, равного данному.
Бирелгән: А
А
О почмагын төзедек.
В
С
О
D
E
Исбатларга: А =
О
Исбатлау: АВС һәм ОDE өчпочмакларын карыйк.
АС=ОЕ, бер әйләнәнең радиуслары буларак.
АВ=ОD, бер әйләнәнең радиуслары буларак.
ВС=DE, бер әйләнәнең радиуслары буларак.
АВС= ОDЕ (3 билге.) А = О
Исбатлау: АВС һәм ОDE өчпочмакларын карыйк.
АС=ОЕ, бер әйләнәнең радиуслары буларак.
АВ=ОD, бер әйләнәнең радиуслары буларак.
ВС=DE, бер әйләнәнең радиуслары буларак.
АВС= ОDЕ (3 билге.) А = О
КҮРСӘТЕРГӘ
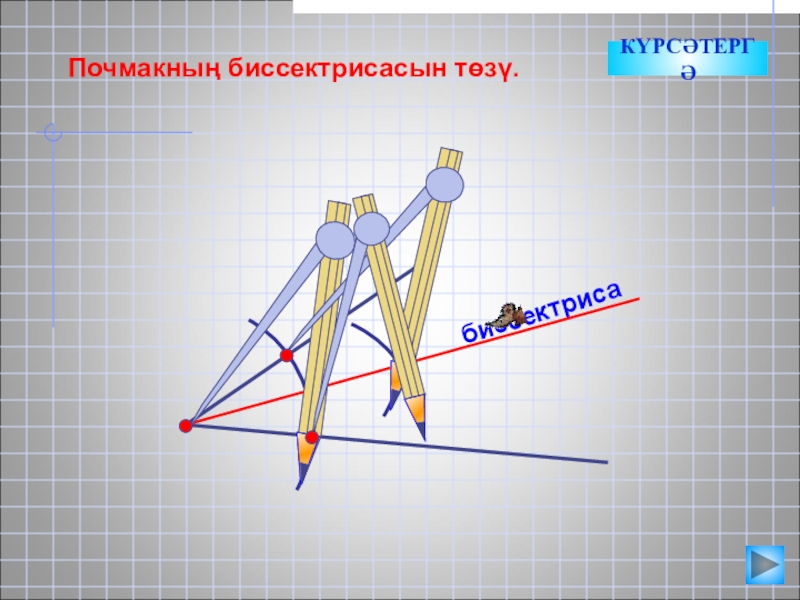
Слайд 11
АВ нуры – А посмагының биссектрисасы икәнен дәлиллик
П Л А Н
Өстәмә төзү.
∆ АСВ и ∆ АDB өчпочмакларының
тигез икәнлеген исбатлыйк.
3. Нәтиҗәләр
Өстәмә төзү.
∆ АСВ и ∆ АDB өчпочмакларының
тигез икәнлеген исбатлыйк.
3. Нәтиҗәләр
А
В
С
D
АС=АD, бер әйләнәнең радиуслары буларак.
СВ=DB, бер әйләнәнең радиуслары буларак.
АВ – уртак як.
?
өчпочмакларның III тигезлек билгесе буенча ∆АСВ = ∆ АDВ
АВ нуры – биссектриса
?
?
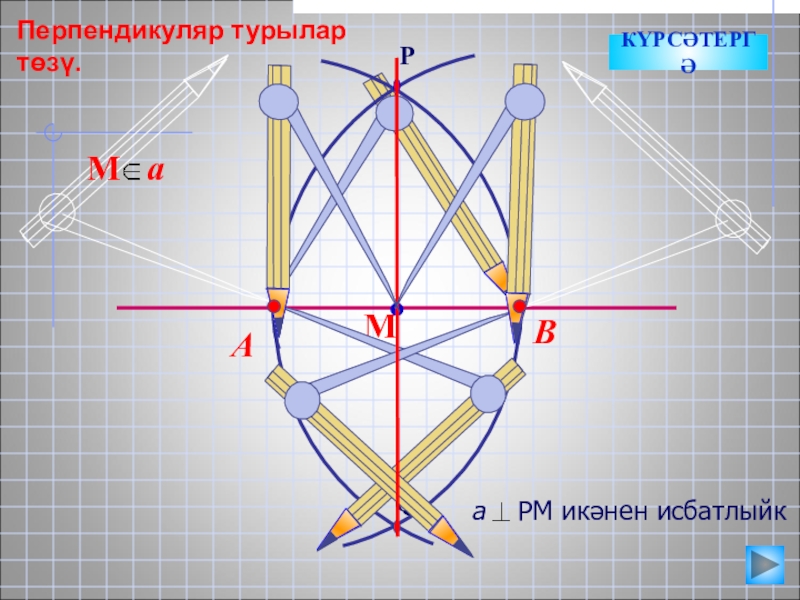
Слайд 13
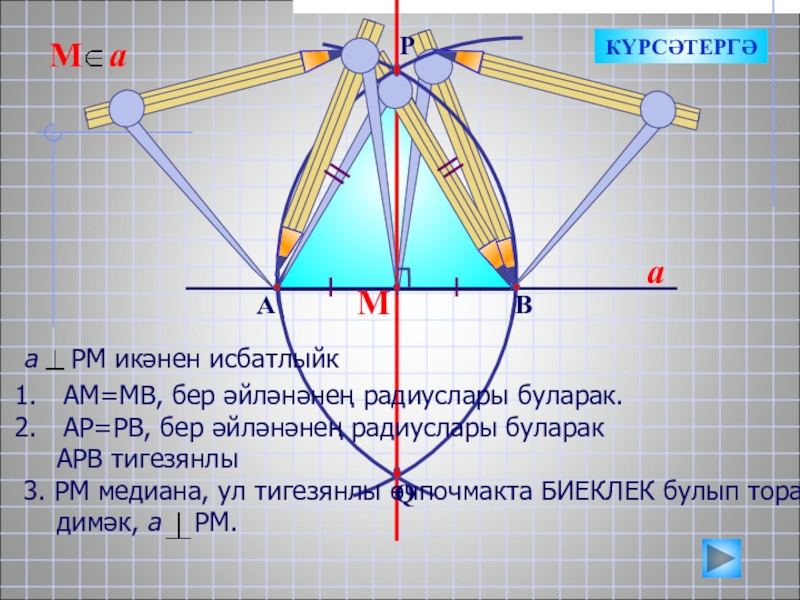
М
a
АМ=МВ, бер әйләнәнең радиуслары буларак.
АР=РВ, бер әйләнәнең радиуслары буларак
АРВ
тигезянлы
3. РМ медиана, ул тигезянлы өчпочмакта БИЕКЛЕК булып тора.
димәк, а РМ.
3. РМ медиана, ул тигезянлы өчпочмакта БИЕКЛЕК булып тора.
димәк, а РМ.
КҮРСӘТЕРГӘ
а РМ икәнен исбатлыйк
Слайд 15
a
N
B
A
C
М
КҮРСӘТЕРГӘ
Циркульләрнең торышларын карыйк.
АМ=АN=MB=BN,
Тигез радиуслар буларак.
МN-уртак як.
3 як
буенча MВN= MAN,
Слайд 17
В
А
АРВ өчпочмагы тигезянлы.
РО - биссектриса, димәк
ул медиана.
Ул вакытта О
ноктасы АВ кисемтәсенең уртасы.
КҮРСӘТЕРГӘ
О –АВ кисемтәсенең уртасы икәнен исбатлыйк
Слайд 18
D
С
Ике ягы һәм почмагы буенча өчпочмак төзү.
Угол hk
h
А нурын карыйк.
P1Q1
га тигез булган АВ кисемтәсе төзик.
Почмакка тигез булган почмак төзибез.
P2Q2 га тигез булган АС кисемтәсе төзик.
Почмакка тигез булган почмак төзибез.
P2Q2 га тигез булган АС кисемтәсе төзик.
В
А
АВС өчпочмагы эзләнелгән өчпочмак.
Бирелгән:
Отрезки Р1Q1 и Р2Q2
Q1
P1
P2
Q2
а
k
КҮРСӘТЕРГӘ
Слайд 21
D
С
Построение треугольника по стороне и двум прилежащим к ней углам.
Угол
h1k1
h2
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному h1k1.
Построим угол, равный h2k2 .
В
А
Треугольник АВС искомый. Обоснуй, используя II признак.
Дано:
Отрезок Р1Q1
Q1
P1
а
k2
КҮРСӘТЕРГӘ
h1
k1
N
Слайд 22
С
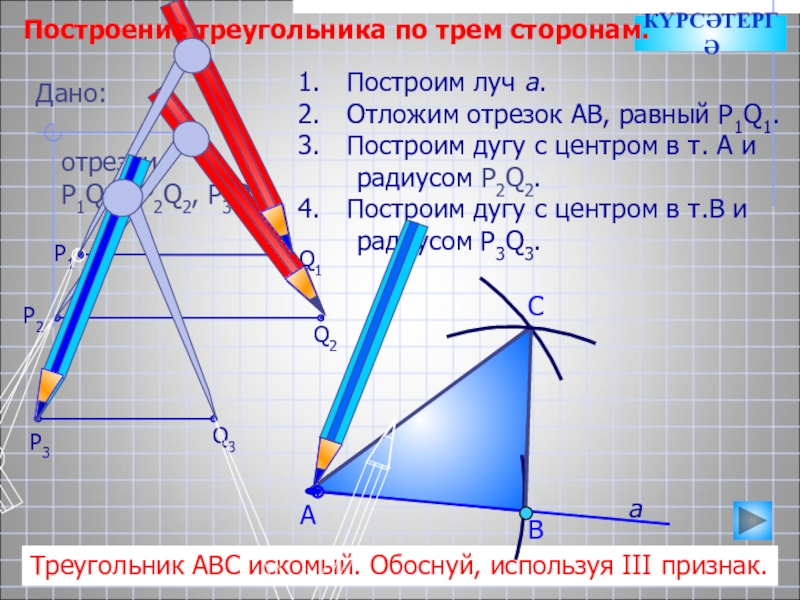
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром в
т. А и
радиусом Р2Q2.
Построим дугу с центром в т.В и
радиусом P3Q3.
радиусом Р2Q2.
Построим дугу с центром в т.В и
радиусом P3Q3.
В
А
Треугольник АВС искомый. Обоснуй, используя III признак.
Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
Q1
P1
P3
Q2
а
P2
Q3
КҮРСӘТЕРГӘ
Построение треугольника по трем сторонам.
Слайд 23 Методы решения задач на
построение
1.Метод анализа.
2.Метод подобия.
3.Метод геометрических мест.
Слайд 24 НЕРАЗРЕШИМЫЕ
ЗАДАЧИ
Квадратура круга
- построение
квадрата , равновеликого
данному кругу с помощью циркуля
и линейки
квадрата , равновеликого
данному кругу с помощью циркуля
и линейки
Слайд 25НЕРАЗРЕШИМЫЕ НЕРАЗРЕШИМЫЕ ЗАДАЧИ
ТРИСЕКЦИЯ УГЛА – деление данного угла на три равных части с помощью циркуля и
линейки.
Слайд 26 НЕРАЗРЕШИМЫЕ
ЗАДАЧИ
УДВОЕНИЕ КУБА
– построение
ребра куба , объем которого вдвое больше объема данного
куба,
с помощью циркуля и линейки.
ребра куба , объем которого вдвое больше объема данного
куба,
с помощью циркуля и линейки.
