- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему 8 сынып геометрия қосымша
Содержание
- 1. 8 сынып геометрия қосымша
- 2. үшбұрышқа іштей сызылған шеңбердің ценрті Үшбұрыштың биссектрисаларының қиылысу нүктесі – үшбұрышқа іштей сызылған шеңбердің ценрті болып табылады.
- 3. үшбұрышқа сырттай сызылған шеңбердің центрі Үшбұрыштың қабырғаларының орта
- 4. үшбұрыштың ауырлық центрі Үшбұрыштың медианаларының қиылысу нүктесі –
- 5. үшбұрыштың ортоцентрі Үшбұрыштың биіктіктерінің қиылысу нүктесі – үшбұрыштың
- 6. Үшбұрыш тамаша нүктелерінің тарихы Аталған төрт нүктеге тек
- 7. Эйлер түзуі 1765 жылы Эйлер кез-келген үшбұрыштың
- 8. Үшбұрыштың Тамаша нүктелерінің арасындағы байланыс Үшбұрышқа сырттай сызылған
- 9. Эйлер Формуласы R – үшбұрышқа сырттай сызылған шеңбердің
үшбұрышқа іштей сызылған шеңбердің ценрті Үшбұрыштың биссектрисаларының қиылысу нүктесі – үшбұрышқа іштей сызылған шеңбердің ценрті болып табылады.
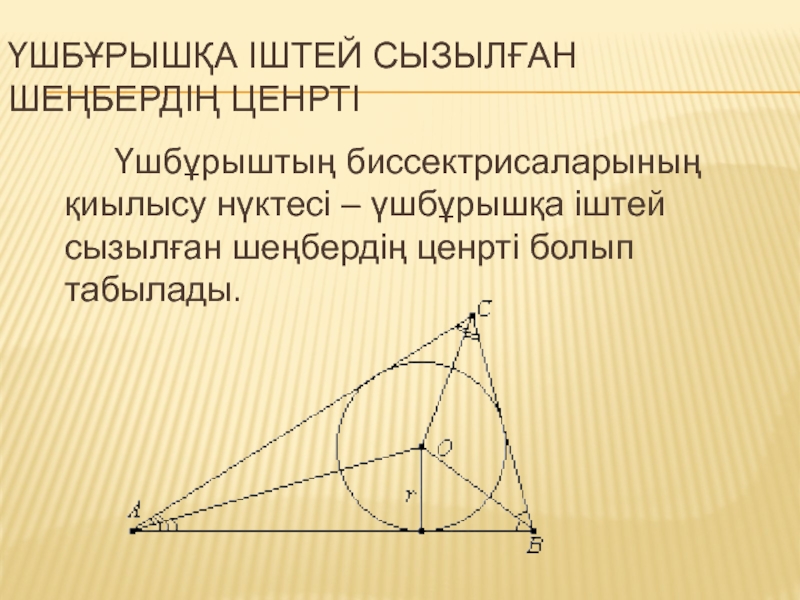
Слайд 2үшбұрышқа іштей сызылған шеңбердің ценрті
Үшбұрыштың биссектрисаларының қиылысу нүктесі – үшбұрышқа іштей
сызылған шеңбердің ценрті болып табылады.
Слайд 3үшбұрышқа сырттай сызылған шеңбердің центрі
Үшбұрыштың қабырғаларының орта перпендикулярларының қиылысу нүктесі –
үшбұрышқа сырттай сызылған шеңбердің центрі болып табылады.
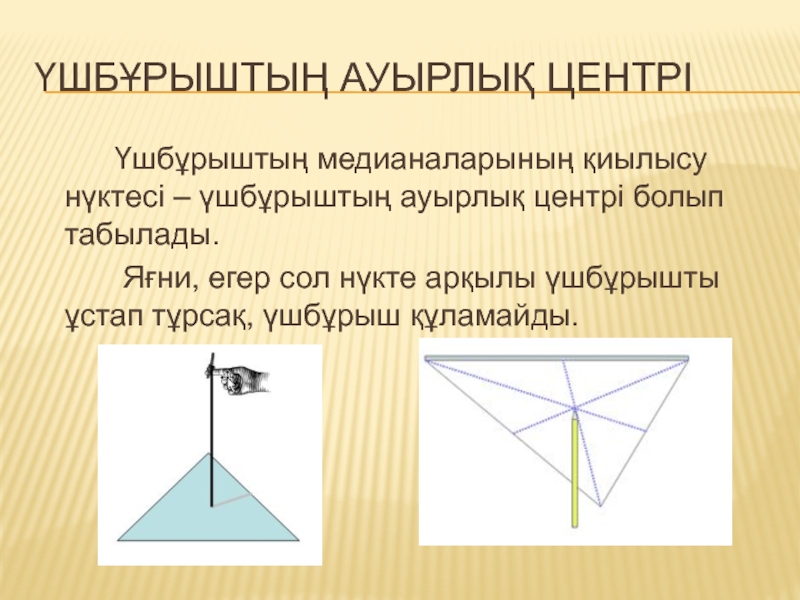
Слайд 4үшбұрыштың ауырлық центрі
Үшбұрыштың медианаларының қиылысу нүктесі – үшбұрыштың ауырлық центрі болып
табылады.
Яғни, егер сол нүкте арқылы үшбұрышты ұстап тұрсақ, үшбұрыш құламайды.
Яғни, егер сол нүкте арқылы үшбұрышты ұстап тұрсақ, үшбұрыш құламайды.
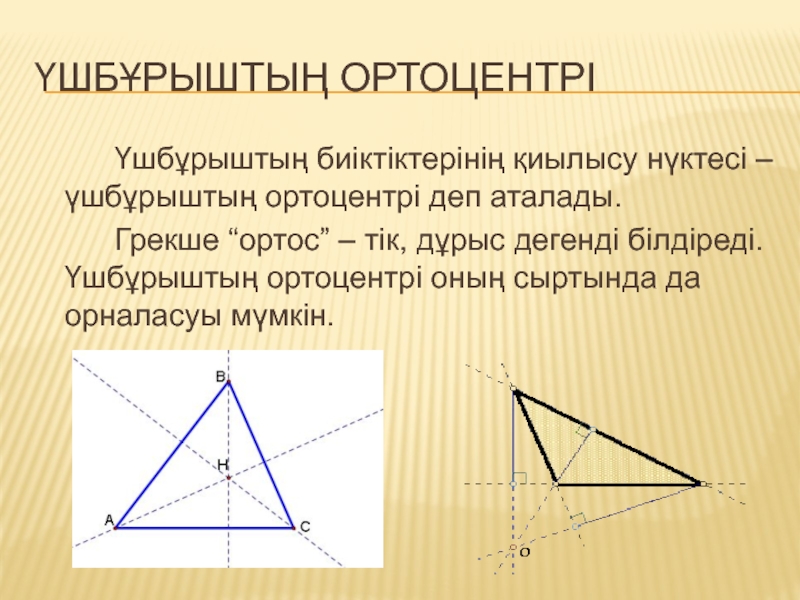
Слайд 5үшбұрыштың ортоцентрі
Үшбұрыштың биіктіктерінің қиылысу нүктесі – үшбұрыштың ортоцентрі деп аталады.
Грекше
“ортос” – тік, дұрыс дегенді білдіреді. Үшбұрыштың ортоцентрі оның сыртында да орналасуы мүмкін.
Слайд 6Үшбұрыш тамаша нүктелерінің тарихы
Аталған төрт нүктеге тек XVIII ғасырдан бастап көңіл
бөлініп, үшбұрышың “ерекше” немесе “тамаша” нүктелері деп атап кетті.
Осы нүктелермен және тағы басқа нүктелермен байланысты үшбұрыштың қасиеттерін зерттеу элементарлық математиканың “үшбұрыш геометриясы” немесе “үшбұрыштың жаңа геометриясы” деген жаңа саланың құрылуына себеп болды.
Оның негізін салушылардың бірі – Л. Эйлер.
Осы нүктелермен және тағы басқа нүктелермен байланысты үшбұрыштың қасиеттерін зерттеу элементарлық математиканың “үшбұрыш геометриясы” немесе “үшбұрыштың жаңа геометриясы” деген жаңа саланың құрылуына себеп болды.
Оның негізін салушылардың бірі – Л. Эйлер.
Слайд 7Эйлер түзуі
1765 жылы Эйлер кез-келген үшбұрыштың ортоцентрі, ауырлық центрі және
оған сырттай сызылған шеңбердің центрі бір нүктеде жататынын дәлелдеді, кейін бұл түзу “Эйлер түзуі” деп аталып кетті.
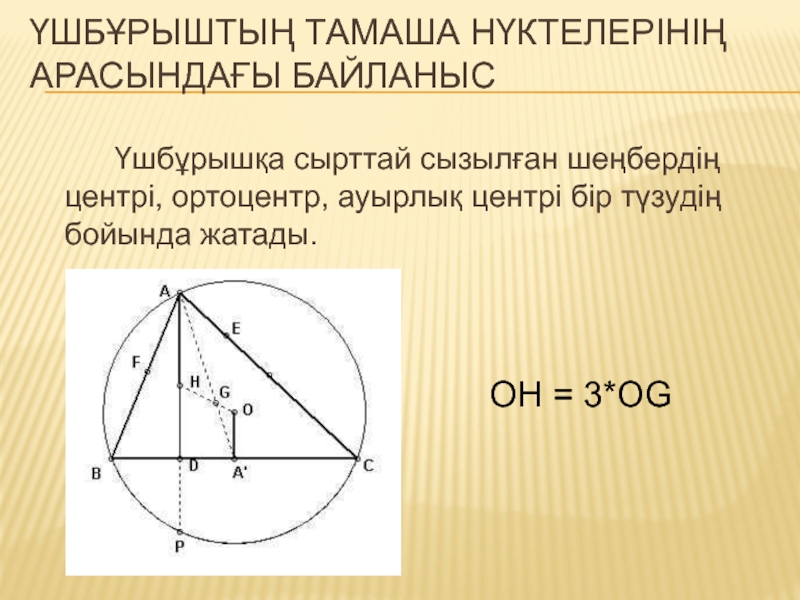
Слайд 8Үшбұрыштың Тамаша нүктелерінің арасындағы байланыс
Үшбұрышқа сырттай сызылған шеңбердің центрі, ортоцентр, ауырлық
центрі бір түзудің бойында жатады.
ОН = 3*OG
Слайд 9Эйлер Формуласы
R – үшбұрышқа сырттай сызылған шеңбердің радиусы, r – үшбұрышқа
іштей сызылған шеңбердің радиусы. Сонда,
Эйлер формуласы деп аталады.
Эйлер формуласы деп аталады.
OI2 = R2 – 2Rr