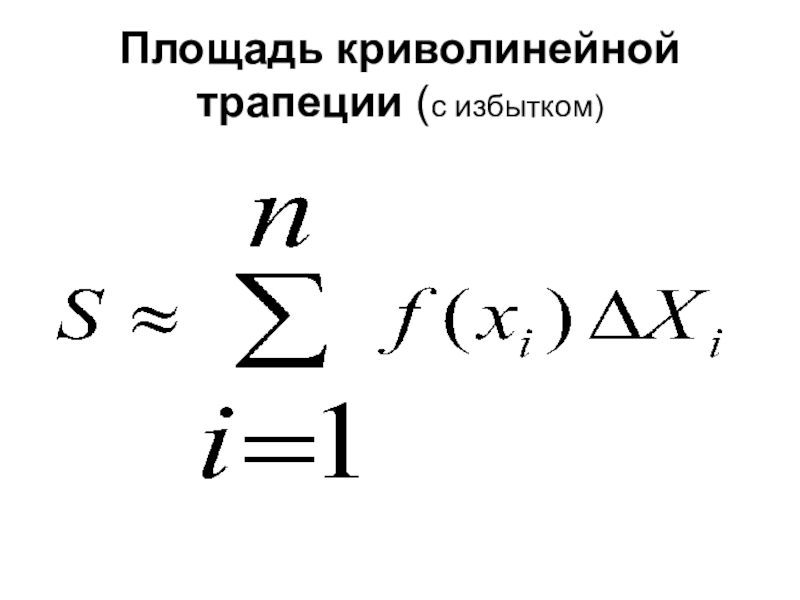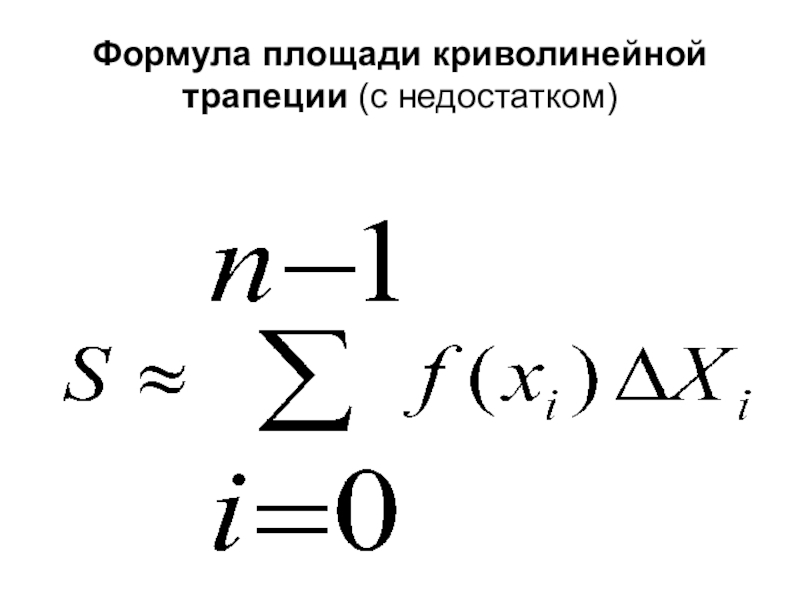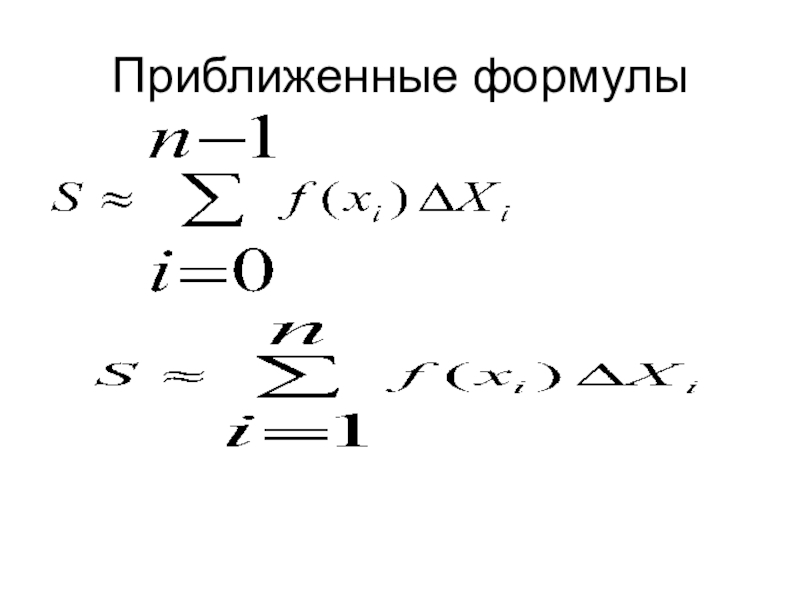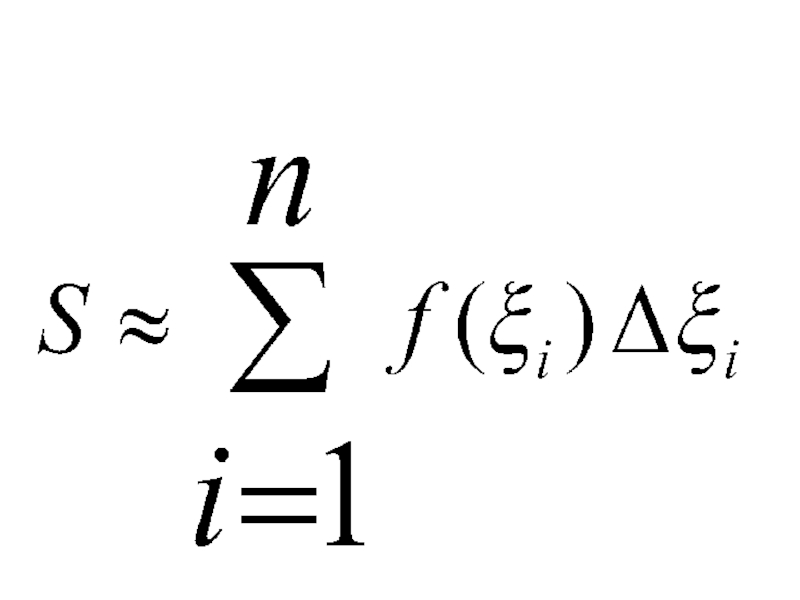- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему : Площадь криволинейной трапеции
Содержание
- 1. : Площадь криволинейной трапеции
- 2. Понятие криволинейной трапеции Пусть дана непрерывная неотрицательная
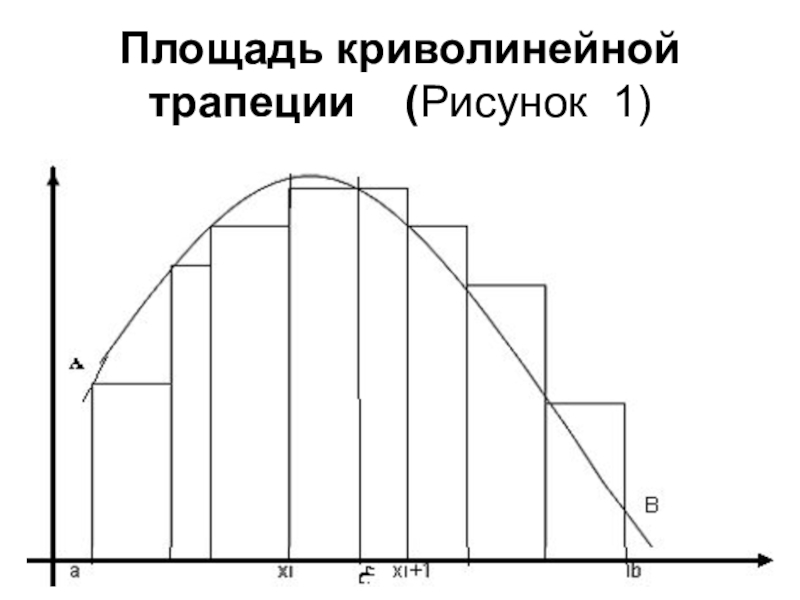
- 3. Площадь криволинейной трапеции (Рисунок 1)
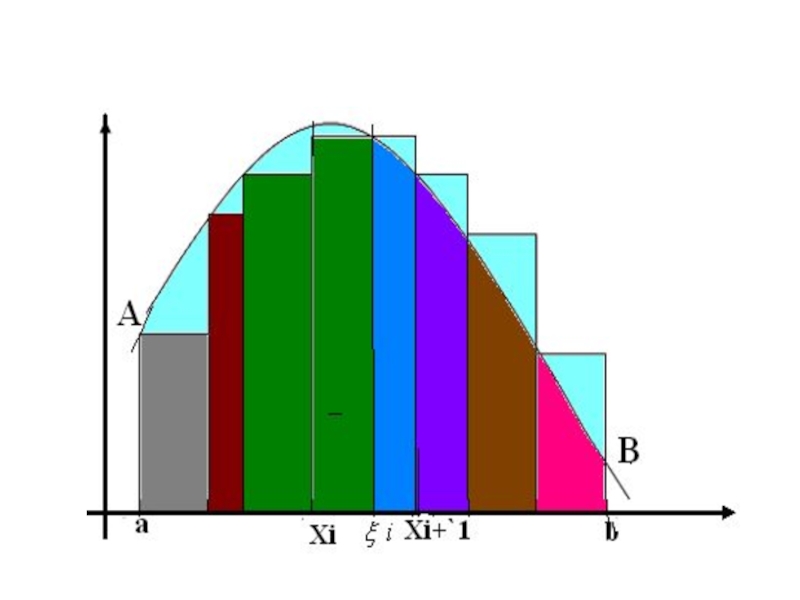
- 4. Слайд 4
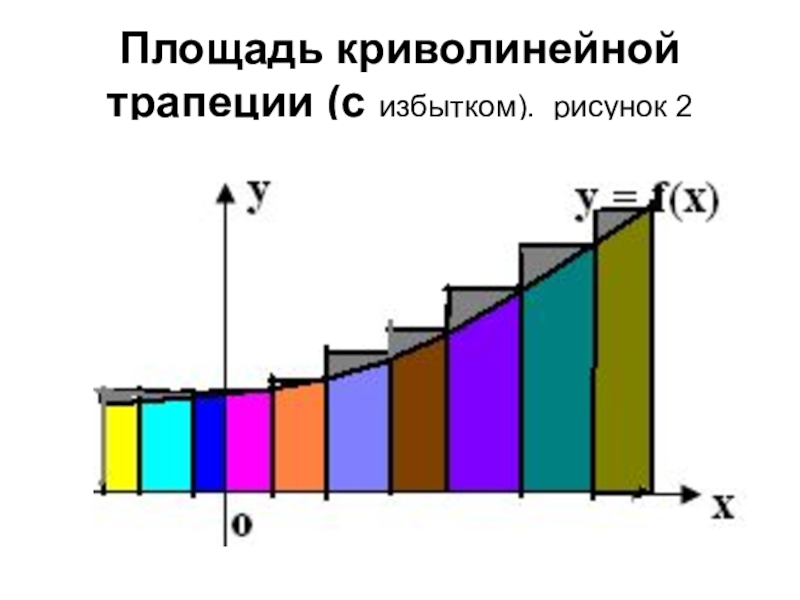
- 5. Площадь криволинейной трапеции (с избытком). рисунок 2
- 6. Площадь криволинейной трапеции (с избытком)
- 7. Определение криволинейной трапеции Фигура, ограниченная неотрицательной
- 8. Площадь криволинейной трапеции
- 9. Формула площади криволинейной трапеции (с недостатком)
- 10. Формула Ньютона-Лейбница
- 11. Приближенные формулы
- 12. Слайд 12
- 13. Определение определенного интеграла
- 14. Определение определенного интеграла
- 15. Слайд 15
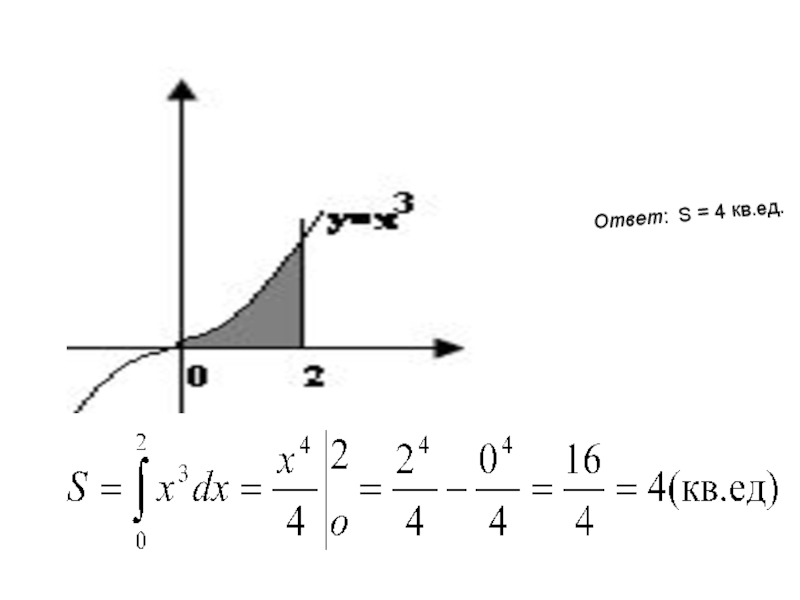
- 16. Найти площадь фигуры, ограниченной кривой
- 17. Ответ: S = 4 кв.ед.
- 18. Замечание
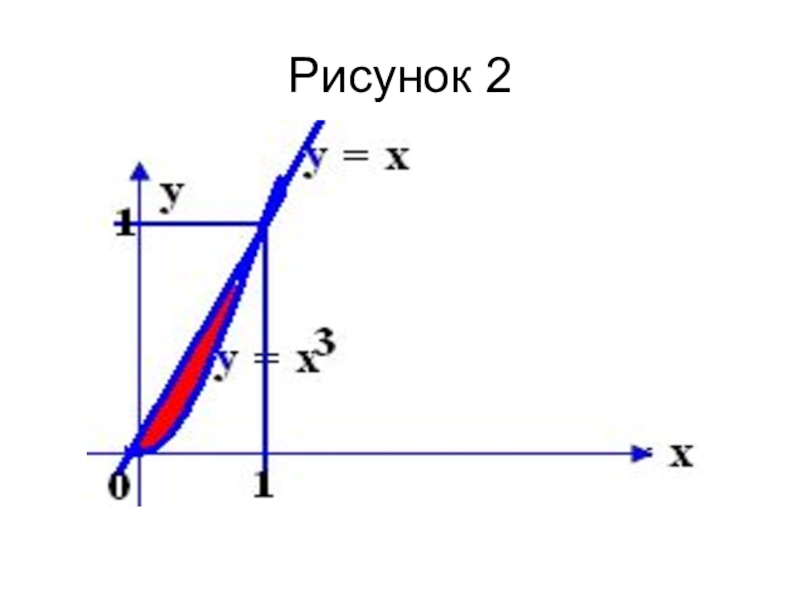
- 19. Пример 2.Найти площадь фигуры, ограниченной кривой у = х3; прямой у = х.
- 20. РешениеФигура, ограниченная кривой у = х3; прямой
- 21. РешениеНо фигура, ограниченная кривой у = х3;
- 22. Фигура, ограниченная прямой у = х; прямыми
- 23. Площадь заштрихованной фигуры равнаразности площади треугольника и
- 24. Рисунок 2
- 25. Решение
- 26. Замечание.Для нахождения пределов интегрирования необходимо найти точки
- 27. Слайд 27
- 28. Пусть дана фигура, ограниченная непрерывными и
- 29. Слайд 29
- 30. поэтому площадь можно вычислить как разность площадей
Понятие криволинейной трапеции Пусть дана непрерывная неотрицательная функция y = f(x) на [a; b] в декартовой системе координат, ограниченная прямыми х=а и х = в, осью ох. Найти площадь фигуры АаbB ( pис.1)
Слайд 1
Понятие криволинейной трапеции. Геометрический смысл определенного интеграла.
Максимова Р.П.
Слайд 2Понятие криволинейной трапеции
Пусть дана непрерывная неотрицательная функция y =
f(x) на [a; b] в декартовой системе координат, ограниченная прямыми х=а и х = в, осью ох. Найти площадь фигуры АаbB ( pис.1)
![Понятие криволинейной трапеции Пусть дана непрерывная неотрицательная функция y = f(x) на [a; b] в декартовой](/img/thumbs/f1d3622cd9f3c0e84dbd14c1111d0ac1-800x.jpg ": Площадь криволинейной трапеции Понятие криволинейной трапеции Пусть дана непрерывная неотрицательная функция y = f(x)")
Слайд 7Определение криволинейной трапеции
Фигура, ограниченная неотрицательной кривой
(у = f
(х) > 0); прямыми
х = а, х = b и осью ОХ
( у = 0) называется криволинейной трапецией. (см рис. 1)
х = а, х = b и осью ОХ
( у = 0) называется криволинейной трапецией. (см рис. 1)
Слайд 16 Найти площадь фигуры, ограниченной кривой у = х3; х =
0; х = 2 и осью 0Х
Решение:. Фигура, ограниченная кривой у = х3; прямыми х = 0; х = 2 и осью 0Х - криволинейная трапеция (по определению), площадь этой фигуры (рис.2) можно вычислить по формуле (1):
Слайд 20Решение
Фигура, ограниченная кривой у = х3; прямой у = х. (см.
рис.3) - не является криволинейной трапецией, поэтому по формуле (1), площадь заштрихованной фигуры (3) нельзя вычислить.
Слайд 21Решение
Но фигура, ограниченная кривой у = х3; прямыми
х =0 и
х=1 –
- криволинейная трапеция, площадь которой можно вычислить по формуле (1)
- криволинейная трапеция, площадь которой можно вычислить по формуле (1)
Слайд 22Фигура, ограниченная прямой у = х; прямыми х = 0 и
х = 1
- криволинейная трапеция. Площадь этой фигуры можно вычислить по формуле площади прямоугольного треугольника (частный случай): площадь прямоугольного треугольника равна половине произведения его катетов:
S = ½ a*b (a u b - катеты).
Слайд 23Площадь заштрихованной фигуры равна
разности площади треугольника и площади криволинейной трапеции, ограниченной
кривой у = х3 , прямыми х=0 и х=1.
Слайд 26Замечание.
Для нахождения пределов интегрирования необходимо найти точки пересечения прямой у =
х и кривой у = х3. Для этого достаточно решить уравнение: х=х3; (левые части равны ( у = у); равны и правые: : х=х3;);
х - х3 = 0; х * (1 – х2) = 0;
х = 0 и х = 1.
х - х3 = 0; х * (1 – х2) = 0;
х = 0 и х = 1.
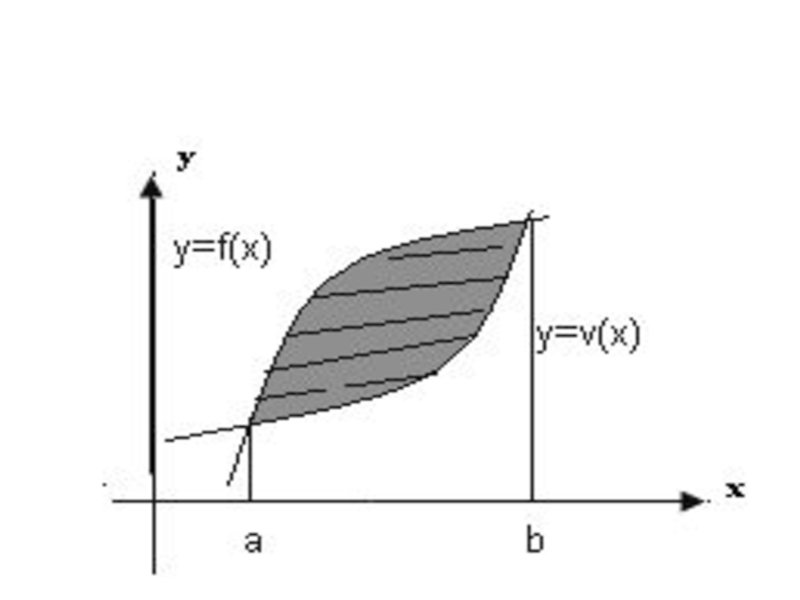
Слайд 28 Пусть дана фигура, ограниченная непрерывными и неотрицательными кривыми
у = f(х) u y =v(x);
Найти площадь этой фигуры.
Решение. Построим чертеж при условии, что кривая у = f(x) > y = v(x); тогда площадь заштрихованной фигуры можно вычислить по формуле (2):
Слайд 30
поэтому площадь можно вычислить как разность
площадей двух криволинейных трапеций,
а именно фигура, ограниченная кривой у = f(x), прямыми х=а и х =b - криволинейная трапеция; именно фигура,
ограниченная кривой у = v(x), прямыми х=а и х = b - криволинейная
