Презентация, доклад по физике Идеальный газ

Содержание

Идеальный газИдеальный газ – модель состояния вещества, в которой относительно его молекул принимаются следующие предположения:Число молекул в газе велико: N >> 1Молекулы не взаимодействуют друг с другомМолекулы газа совершают неупорядоченное, хаотичное движение.

Слайд 1Идеальный газ
КПК "Теория и методика обучения физики в общеобразовательных учреждениях

Идеальный газ КПК

Слайд 2Идеальный газ
Идеальный газ – модель состояния вещества, в которой относительно его молекул

принимаются следующие предположения:
Число молекул в газе велико: N >> 1
Молекулы не взаимодействуют друг с другом
Молекулы газа совершают неупорядоченное, хаотичное движение.

Идеальный газИдеальный газ – модель состояния вещества, в которой относительно его молекул принимаются следующие предположения:Число молекул в газе

Слайд 3Модель идеальных газов
среднее расстояние между отдельными молекулами много больше их размеров

(d >> a), или объем, занимаемый молекулами такого газа, несравнимо мал по сравнению с объемом сосуда, который они заполняют;
температура газа достаточно высока (при нормальной концентрации n = 3·1025 м-3 температура T > 10 K считается высокой).
молекулы не притягиваются друг к другу, т.е. условия достаточно далеки от условий перехода газа в жидкость.


Модель идеальных газовсреднее расстояние между отдельными молекулами много больше их размеров (d >> a), или объем, занимаемый

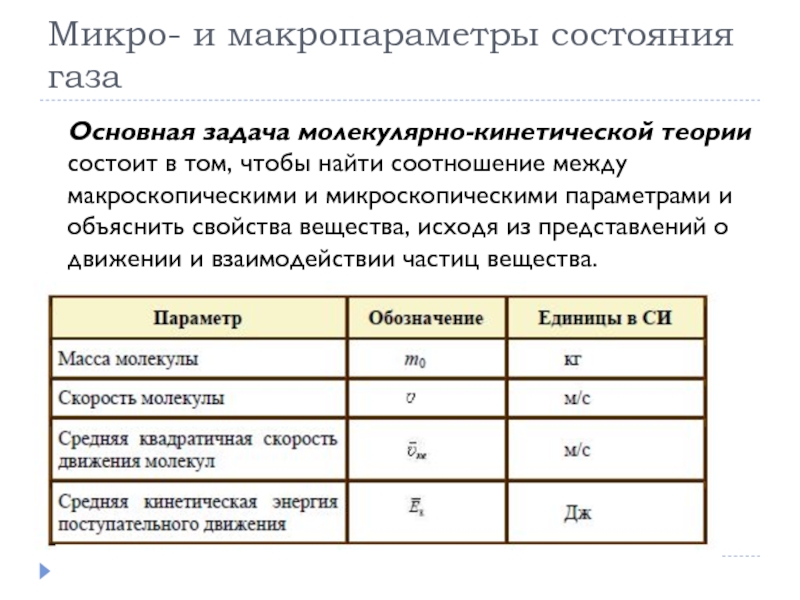
Слайд 4Микро- и макропараметры состояния газа
Основная задача молекулярно-кинетической теории состоит в том,

чтобы найти соотношение между макроскопическими и микроскопическими параметрами и объяснить свойства вещества, исходя из представлений о движении и взаимодействии частиц вещества.
Микро- и макропараметры состояния газаОсновная задача молекулярно-кинетической теории состоит в том, чтобы найти соотношение между макроскопическими и

Слайд 5Микро- и макропараметры состояния газа

Микро- и макропараметры состояния газа

Слайд 6Средняя квадратичная скорость и средняя кинетическая энергия молекул


где N – число молекул в

газе.
Величина  называется средней квадратичной скоростью молекул в газе.
Лабораторная работа «Расчет средних квадратичных скоростей молекул»
(«Физика в системе Д.Б. Эльконина - В.В. Давыдова», 7-9 класс)


Средняя квадратичная скорость и средняя кинетическая энергия молекулгде N – число молекул в газе.Величина 

Слайд 7Средняя кинетическая энергия молекул

Средняя кинетическая энергия молекул

Слайд 8Основное уравнение молекулярно-кинетической теории идеального газа
Уравнение связывает макропараметры системы – давление p и

концентрацию молекул с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:
или

тогда формула для давления примет вид

Основное уравнение молекулярно-кинетической теории идеального газаУравнение связывает макропараметры системы – давление p и концентрацию

Слайд 9Температура. Абсолютная температура
Понятие «температура» - степень нагретости тела не по субъективным

ощущениям экспериментатора, а на основании объективных показаний физических приборов.
Термометр – прибор для измерения температуры, действие которого основано на взаимно-однозначной связи наблюдаемого параметра системы (давления, объема, электропроводности, яркости свечения и т.д.) с температурой
Температура. Абсолютная температураПонятие «температура» - степень нагретости тела не по субъективным ощущениям экспериментатора, а на основании объективных

Слайд 10Температура. Абсолютная температура
Для калибровки термометра необходимы тела, температура которых считается неизменной

и воспроизводимой. Обычно это температура равновесной системы лед – вода при нормальном давлении (0 °С) и температура кипения воды при нормальном давлении (100 °С).

Температура. Абсолютная температураДля калибровки термометра необходимы тела, температура которых считается неизменной и воспроизводимой. Обычно это температура равновесной

Слайд 11Термодинамическое (тепловое) равновесие
Температура, как термодинамический параметр, характеризует состояние теплового равновесия. Для

измерения температуры необходим контакт с термодинамической системой, температуру которой измеряют.
Термодинамическое (тепловое) равновесие – состояние макросистемы, при котором макропараметры остаются сколь угодно долго неизменными.
Термодинамическое (тепловое) равновесиеТемпература, как термодинамический параметр, характеризует состояние теплового равновесия. Для измерения температуры необходим контакт с термодинамической

Слайд 12Температура – мера средней кинетической энергии поступательного движения молекул
температура – мера

средней кинетической энергии поступательного движения молекул


средней квадратичной скорость
Температура – мера средней кинетической энергии поступательного движения молекултемпература – мера средней кинетической энергии поступательного движения молекулсредней

Слайд 13Температура – мера средней кинетической энергии поступательного движения молекул
Средняя кинетическая энергия

поступательного движения молекул связана с температурой Т соотношением:

где k = 1,38∙10–23 Дж/К – постоянная Больцмана.

Температура – мера средней кинетической энергии поступательного движения молекулСредняя кинетическая энергия поступательного движения молекул связана с температурой

Слайд 14Основное уравнение молекулярно – кинетической теории идеального газа
Средняя квадратичная скорость характеризует

скорость хаотического движения молекул, называемого еще тепловым движением.
Связь между давлением, концентрацией и температурой для идеального газа можно получить, исключив из равенств среднюю кинетическую энергию



Основное уравнение молекулярно – кинетической теории идеального газаСредняя квадратичная скорость характеризует скорость хаотического движения молекул, называемого еще

Слайд 15Парциальное давление. Закон Дальтона
Если имеется смесь нескольких идеальных газов, то для

каждого газа можно записать уравнение, где ni – концентрация молекул i-го газа,  – давление, которое производил бы этот газ, если бы он один занимал весь сосуд. Это давление называют парциальным давлением газа (англ. partial – частичный).
Суммарное давление смеси равно сумме давлений, которое оказывал бы каждый из газов, помещенный в тот же сосуд отдельно от остальных:
p = p1+ p2+ …+ pn
Скорости и энергии молекул в смеси газов 

Парциальное давление. Закон ДальтонаЕсли имеется смесь нескольких идеальных газов, то для каждого газа можно записать уравнение, где

Слайд 16Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)
pV = vRT
где R = 8,31

Дж/(K·моль) – универсальная газовая постоянная,
m – масса газа
 M – молярная масса газа
Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:


Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)pV = vRTгде R = 8,31 Дж/(K·моль) – универсальная газовая постоянная,m – масса газа M – молярная

Слайд 17Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)
Плотность газа не постоянна,

а определяется его давлением и температурой.
Для смеси различных газов, находящихся в равновесии, уравнение можно записать в виде:


где давление смеси (pi – парциальное давление i-го компонента)
– масса смеси (mi – масса i - го компонента)

– средняя молярная масса смеси.

Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)Плотность газа не постоянна, а определяется его давлением и температурой.

Слайд 18Равновесные процессы
Равновесный процесс – квазистатический процесс
Если процесс с идеальным газом (или

любой термодинамической системой) идет достаточно медленно, то давление и температура газа во всем его объеме успевают выровняться и принимают в каждый момент времени одинаковые по всему объему значения. Это означает, что газ проходит через последовательность равновесных (почти равновесных) состояний.
Такой процесс с газом называется равновесным.
Равновесные процессыРавновесный процесс – квазистатический процессЕсли процесс с идеальным газом (или любой термодинамической системой) идет достаточно медленно,

Слайд 19Объединённый газовый закон

Объединённый газовый закон

Слайд 20Закон Бойля–Мариотта
1 случай:
T = const – изотермический процесс;
m = const;
pV =

const – закон Бойля–Мариотта.

При постоянной массе идеального газа и постоянной температуре, произведение давления на его объем есть величина постоянная.

Закон Бойля–Мариотта1 случай:T = const – изотермический процесс;m = const;pV = const – закон Бойля–Мариотта.При постоянной массе

Слайд 21Изотермы в координатах (p, V), (V, T) и (p, T)
Графики изотермического

процесса







Демонстрационная модель "Тепловые процессы: изотермический процесс«
Анимационная модель по теме "Изотермический процесс"

Изотермы в координатах (p, V), (V, T) и (p, T)Графики изотермического процессаДемонстрационная модель

Слайд 22Закон Гей-Люссака
p = const – изобарный процесс;
m = const;
V/T = const

– закон Гей-Люссака.

При постоянной массе идеального газа и постоянном давлении, отношение его объема к температуре есть величина постоянная.

Закон Гей-Люссакаp = const – изобарный процесс;m = const;V/T = const – закон Гей-Люссака.При постоянной массе идеального

Слайд 23Изобары в координатах (p, V), (p, T) и (V, T)
Графики изобарного

процесса






Демонстрационная модель "Тепловые процессы: изобарический процесс«
Анимационная модель по теме "Изобарный процесс"









Изобары в координатах (p, V), (p, T) и (V, T)Графики изобарного процессаДемонстрационная модель

Слайд 24Закон Шарля
V = const – изохорный процесс;
m = const;
p/T = const

– закон Шарля.
 
При постоянной массе идеального газа и постоянном объеме отношение давления к температуре есть величина постоянная.

Закон ШарляV = const – изохорный процесс;m = const;p/T = const – закон Шарля. При постоянной массе идеального

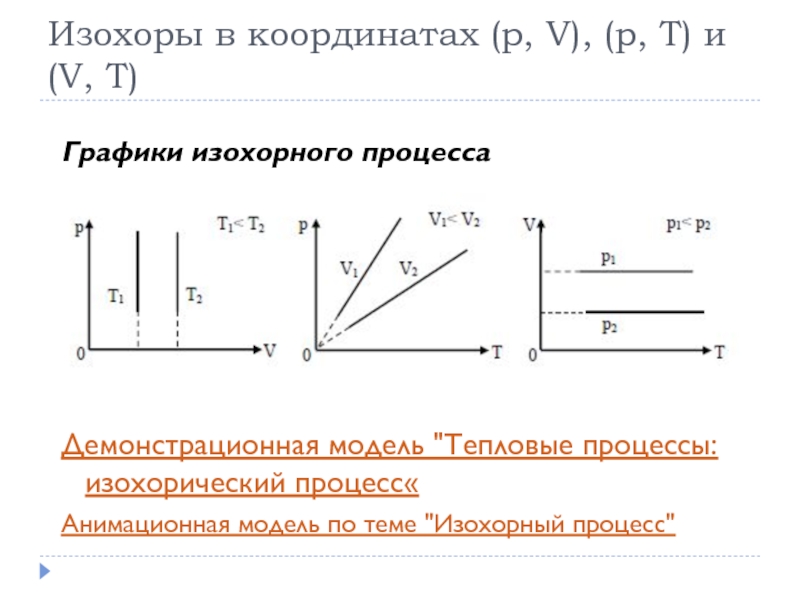
Слайд 25Изохоры в координатах (p, V), (p, T) и (V, T)
Графики изохорного

процесса






Демонстрационная модель "Тепловые процессы: изохорический процесс«
Анимационная модель по теме "Изохорный процесс"
Изохоры в координатах (p, V), (p, T) и (V, T)Графики изохорного процессаДемонстрационная модель

Слайд 26Методические указания по решению задач
Решение задач на расчет микропараметров газа осуществляется

на основании основного уравнения молекулярно–кинетической теории идеального газа, формулы для расчета среднего значения кинетической энергии молекулы и определения абсолютной температуры.
Методические указания по решению задачРешение задач на расчет микропараметров газа осуществляется на основании основного уравнения молекулярно–кинетической теории

Слайд 27Методические указания по решению задач
Две группы задач:
задачи, в которых заданы параметры

газа в начальном состоянии и некоторые параметры в конечном состоянии при постоянной массе
задачи, где в условиях фигурирует масса газа и приведены некоторые параметры состояния или рассматриваются такие процессы, в которых масса газа изменяется. Необходимо найти неизвестные величины.
Методические указания по решению задачДве группы задач:задачи, в которых заданы параметры газа в начальном состоянии и некоторые

Слайд 28Задачи первой группы
Если при постоянной массе в результате перехода из начального

состояния в конечное один из параметров газа не меняется, то при решении задач можно пользоваться соответствующим законом одного из изопроцессов.
Если меняются все три параметра, следует применять уравнение Менделеева – Клапейрона. При этом необходимо также использовать дополнительные условия в виде вспомогательных формул и выразить, где это необходимо, давление и объем через другие заданные величины.

Задачи первой группыЕсли при постоянной массе в результате перехода из начального состояния в конечное один из параметров

Слайд 29Задачи второй группы
При решении задач второй группы чаще всего бывает необходимо

определить один из параметров состояния газа.
В этом случае пользуются уравнением Клапейрона – Менделеева с учетом дополнительных условий.
В случае смеси газов необходимо воспользоваться ещё и законом Дальтона.
Если в задаче рассматривается процесс смешения газов, находящихся в разных сосудах, следует различать парциальные давления от давлений, оказываемых газами на стенки сосудов, которые они занимали первоначально.

Задачи второй группыПри решении задач второй группы чаще всего бывает необходимо определить один из параметров состояния газа.

Слайд 30Примеры решения задач
Задача 1
В сосуде находится смесь 20 г углекислого газа

и 30 г азота. Найти плотность этой смеси при температуре 27°С и давлении 200 кПа. Газы считать идеальными.

Примеры решения задачЗадача 1В сосуде находится смесь 20 г углекислого газа и 30 г азота. Найти плотность

Слайд 31Задача 1

Задача 1

Слайд 32Задача 2
Одна треть молекул азота, заключенного в закрытый сосуд, распалась на

атомы вследствие термической диссоциации при повышении температуры от 70С до 14070С. Во сколько раз при этом возросло давление газа?

Задача 2Одна треть молекул азота, заключенного в закрытый сосуд, распалась на атомы вследствие термической диссоциации при повышении

Слайд 33Задача 2

Задача 2

Слайд 34Задача 3
Идеальный газ изотермически сжимают, затем изобарически нагревают и изохорически возвращают

в исходное состояние.
Нарисовать графики этого равновесного процесса в координатах (p, V); (V, T); (p, T).

Задача 3Идеальный газ изотермически сжимают, затем изобарически нагревают и изохорически возвращают в исходное состояние. Нарисовать графики этого

Слайд 35Задача 3

Задача 3
Скачать презентацию

Похожие презентации

Презентация по физике на тему Основные положения МКТ (10 класс) Презентация по физике на тему Основные положения МКТ (10 класс) 196
Презентация по физике на тему Источники тока. Электрическая цепь (9 класс) Презентация по физике на тему Источники тока. Электрическая цепь (9 класс) 161
Презентация по физике на тему Манометры Презентация по физике на тему Манометры 277
Презентация по физике Воздухоплавание Презентация по физике Воздухоплавание 165
Звуковые колебания. Звуковые колебания. 283
Тестовая работа по физике 8 класса по теме: Тепловое движение. Температура. Внутренняя энергия. Тестовая работа по физике 8 класса по теме: Тепловое движение. Температура. Внутренняя энергия. 272

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть