- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку повторения Нестандартные задачи приподготовке к ЕГЭ по физике
Содержание
- 1. Презентация к уроку повторения Нестандартные задачи приподготовке к ЕГЭ по физике
- 2. Стандартный подход к решению нестандартных задач по физике.
- 3. Пояснительная записка.Решение нестандартных, т.е. сложных задач –
- 4. План:1. Применение производной в задачах на экстремум.2.
- 5. Применение производной в задачах на экстремум.Задача №1.Частица
- 6. Задача №2.Стартовав, автомобиль набирает скорость, а затем
- 7. Время ускоренного движения до первой контрольной отметки
- 8. Задача №3.Составляется электрическая цепь из двух параллельно
- 9. График функции r(R1) имеет вид:rR1R1 = R/2
- 10. Задача №4.ЭДС источника тока равна ε, а
- 11. Задача №5.Мальчик переплывает реку с одного берега
- 12. Применение векторных диаграмм. Задача №1.Предыдущую задачу о
- 13. Задача №2.Под каким углом нужно тянуть за
- 14. Пусть теперь требуется найти наименьшую силу, сообщающую
- 15. Задача №3.Кот Леопольд сидел у края крыши.
- 16. Удачный выбор системы отсчета.Задача №1.Человек находится в
- 17. Нетрудно сообразить, что эта задача эквивалентна задаче
- 18. Задача №2.Автомобили А и В движутся равномерно
- 19. Задача №3.Массивная стальная плита движется вверх со
- 20. Задача №4.Один электрон движется со скоростью v
- 21. Задача №1.Поезд движется прямолинейно вправо с постоянным
- 22. Задача №2.На гладкой горизонтальной поверхности находится призма
- 23. Так как Fи = ma, то
- 24. Задача №3.На поверхности Земли на широте φ
- 25. Общий метод решения задач на колебательные движения.
- 26. Задача №2.На двух вращающихся в противоположные стороны
- 27. Задача №3.ΔmxxВ сообщающиеся сосуды U-образной формы налита
- 28. Задача №4.mg∙cosα αxПредставьте себе, что в земном
- 29. Применение законов Кеплера.Задача №1.ЗемляСолнцеаОцените время свободного падения
- 30. Задача №2.На большом расстоянии от Земли метеорит
- 31. При движении метеорита в поле тяжести Земли
- 32. Применение принципа симметрии для решения задач. Задача
- 33. В ситуациях (2), (3), (4) напряженность поля
- 34. Задача №2.Поверхность полусферической чаши радиусом R с
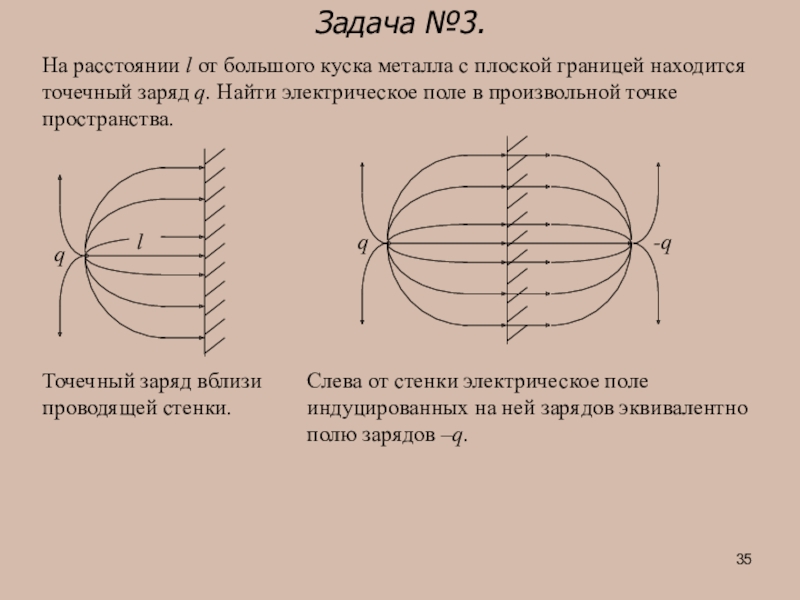
- 35. Задача №3.На расстоянии l от большого куска
- 36. Прежде всего ясно, что в толще металла
- 37. q-qσ = E ε0Заряд q притягивается к
- 38. Задача №4.Две звезды массами m1 и m2
- 39. Выводы.Умение решать задачи является и средством, и
Слайд 3Пояснительная записка.
Решение нестандартных, т.е. сложных задач – процесс творческий, требующий не
Анализируя решения сложных задач, мы видим, что в них нестандартные ситуации сводятся к стандартным, и для их описания используются всем известные алгоритмы, не выходящие за пределы школьной программы.
Рассмотрим несколько примеров алгоритмов, лежащих «на грани» школьной физики, поэтому используемых мало.
Слайд 4План:
1. Применение производной в задачах на экстремум.
2. Применение векторных диаграмм.
3. Удачный
4. Системы отсчета, движущиеся с ускорением. Сила инерции.
5. Общий метод решения задач на колебательные движения.
6. Применение законов Кеплера.
7. Применение принципа симметрии для решения задач.
Слайд 5Применение производной в задачах на экстремум.
Задача №1.
Частица пролетает расстояние l равномерно,
Дано: l, a, tmin. v - ?
Решение:
А
В
=const
l
= 0
Очевидно, что полное время движения частицы t складывается из времени равномерного движения t1=l/v, где v – искомая скорость, и времени торможения t2=v/a;
, где v > 0.
t'(v) = 0 при v2 – la = 0, откуда
Слайд 6Задача №2.
Стартовав, автомобиль набирает скорость, а затем выходит на первую контрольную
Дано: S, μ. tmin - ?
Решение:
A
1
2
S
=const
Слайд 7Время ускоренного движения до первой контрольной отметки будет минимальным, если автомобиль
μmg = ma, a = μg, v = at1
– время разгона,
– время движения от 1 до 2,
, откуда
Слайд 8Задача №3.
Составляется электрическая цепь из двух параллельно соединенных сопротивлений R1 и
Дано: R1, R2, R, rmax. R1/R2 - ?
Решение:
R1 + R2 = R
R2 = R – R1;
; r'(R1) = 0 при R – 2R1 = 0
Слайд 9График функции r(R1) имеет вид:
r
R1
R1 = R/2
Значит, R1 = R/2
Слайд 10Задача №4.
ЭДС источника тока равна ε, а внутреннее сопротивление равно r.
Дано: ε, r. Pmax - ? R - ? η - ?
Решение:
Полезная мощность P равна:
P(R) имеет максимальное значение при условии, что имеет максимальное зачение.
y'(R) = 0 при R = r, значит Pmax = ε2/4r2;
Максимальному значению полезной мощности соответствует η = R/2R = 0,5.
Слайд 11Задача №5.
Мальчик переплывает реку с одного берега на другой. Его скорость
Дано: , , Smin. α - ?
Решение:
S
О
α
y
x
H
y = v∙sinα∙t
x = (u - v∙cosα)t
При y = H, t = H/sinα – время переправы.
x’(α) = 0 при v2 = uv∙cosα;
cosα = v/u;
α = arccos(v/u).
Слайд 12Применение векторных диаграмм.
Задача №1.
Предыдущую задачу о переправе через реку можно
α
x
S
y
= + – скорость относительно берега.
Конец вектора может лежать на окружности с радиусом v и центром в конце вектора u.
Из рисунка видно, что снос будет минимальным, если V направлена по касательной к окружности. При этом v перпендикулярен V. Следовательно cosα = v/u.
В этом случае скорость пловца относительно воды также будет минимальной.
Слайд 13Задача №2.
Под каким углом нужно тянуть за веревку тяжелый ящик, чтобы
Дано: μ, Fmin. α - ?
Решение:
α
φ
При минимальном значении силы тяги = 0 и
+
+
+
= 0
Заменим
+
=
.
Тогда
+
+
= 0.
Построим векторную диаграмму сил в соответствии с уравнением:
φ
α
Как видно из рисунка, величина силы будет минимальной, когда её направление будет перпендикулярно вектору . Тогда α = φ,
φ = arctg μ.
Слайд 14Пусть теперь требуется найти наименьшую силу, сообщающую ящику заданное ускорение
В этом случае
+
+
=
.
Построим векторную диаграмму, соответствующую этому уравнению:
φ
α
И в этом случае вектор перпендикулярен вектору и составляет угол α с горизонтом.
α = arctg μ.
Нетрудно доказать, что если ящик тянуть вверх по наклонной плоскости под углом к ней, то сила F будет минимальной при условии, что её направление составляет угол α = arctg μ с наклонной плоскостью.
α
α
φ
Слайд 15Задача №3.
Кот Леопольд сидел у края крыши. Два озорных мышонка выстрелили
Дано: τ, . S - ?
Решение:
90˚
А
В
S
=
+
Этому уравнению соответствует векторная диаграмма:
90˚
Из рисунка следует
. Тогда
Слайд 16Удачный выбор системы отсчета.
Задача №1.
Человек находится в поле на расстоянии l
Дано: u, v, l. α - ?
Решение:
α
D
B
C
A
Smin
α
l
В каком направлении следует бежать человеку? Оказывается, что на этот вопрос легко ответить, если перейти в другую систему отсчета, в которой автобус покоится. В данной СО неподвижно стоящий на земле человек имеет скорость u, направленную вправо, а полная скорость человека равна V=u+v.
Слайд 17Нетрудно сообразить, что эта задача эквивалентна задаче о минимальном сносе переплывающего
Требование выбежать на шоссе как можно дальше от автобуса равносильно требованию минимального сноса при переправе через реку. Поэтому искомое направление вектора v определяется таким же направлением, как и в той задаче.
sinα = v/u; α = arcsin(v/u).
Таким образом, бежать к шоссе нужно не по кратчайшему пути, а под углом α к нему.
Из рисунка видно, что человек сможет прибежать на шоссе раньше автобуса только в том случае, если в начальный момент автобус находится от точки В на расстоянии не меньшем
Рассмотренная задача показывает, как удачный выбор СО позволяет значительно облегчить решение.
Рассмотрим еще несколько аналогичных примеров.
Слайд 18Задача №2.
Автомобили А и В движутся равномерно с одинаковыми скоростями по
Дано: v, α, AO = a, BO = b. Smin - ?
Решение:
B
1
2
3
B’
A1
B1
A
Рассмотрим движение автомобиля В относительно автомобиля А. Его скорость в этой СО равна
и постоянна по величине и направлению. Это значит, что относительно автомобиля А автомобиль В движется по прямой линии 3.
Наименьшее расстояние между автомобилями равно АВ’.
Для того, чтобы изобразить положение отрезка АВ’ в неподвижной СО, сместим его параллельно самому себе так, чтобы конец B’ попал на дорогу 2. Таким образом, точки А1 и В1 являются искомыми положениями автомобилей:
Слайд 19Задача №3.
Массивная стальная плита движется вверх со скоростью v. На её
Дано: v, h. H - ?
Решение:
Столкновение шарика с плитой рассмотрим в системе отсчета, связанной с плитой. В этой СО скорость шарика в момент столкновения равна . Так как столкновение шарика с плитой упругое, то после столкновения направление вектора его скорости относительно плиты изменится на противоположное. Относительно Земли скорость шарика становится равной
а высота подъема относительно точки удара будет равна
,
Слайд 20Задача №4.
Один электрон движется со скоростью v к другому свободному электрону.
Дано: v. rmin - ?
Решение:
В системе отсчета, связанной с центром масс электроны движутся навстречу друг другу с одинаковыми по модулю скоростями
|v1| = |v2| = v/2
Минимальное расстояние r между ними найдём условия сохранения энергии: начальное значение кинетической энергии электронов равно конечному значению потенциальной энергии:
Слайд 21Задача №1.
Поезд движется прямолинейно вправо с постоянным ускорением . Какой
Дано: l, . α - ? T - ?
Решение:
Поезд движется вправо. Тогда на мятник будет действовать сила инерции , направленная влево (m – масса маятника). Складываясь с силой , направленной вниз, она дает силу .
α
Значит, маятник будет вести себя так, будто сила тяжести направлена не вниз, а вдоль вектора . Угол отклонения его от вертикали равен
Период его колебаний будет равен:
Колебания этого маятника будут совершаться не около вертикали, а около «кажущейся» вертикали, определяемой направлением вектора .
Системы отсчета, движущиеся с ускорением. Сила инерции.
Слайд 22Задача №2.
На гладкой горизонтальной поверхности находится призма массой M с углом
Дано: μ > tgα, = bt, = 0. S - ?
Решение:
y
x
= 0
α
При = 0 уравнение равновесия бруска относительно призмы будет иметь вид:
mg∙sinα + Fи∙cosα – μN = 0
N + Fи∙sinα – mg∙cosα = 0
Из этой системы найдём Fи:
Слайд 23Так как Fи = ma, то
Согласно II закону Ньютона ускорение движения призмы с бруском равно:
, откуда найдем время движения призмы:
Путь, пройденный призмой за это время, равен S = Δx = x при x0 = 0, где Δx – изменение координаты призмы.
Так как a = v’, найдем v. Она является первообразной для ускорения.
Если
,то
Так как v = x’, найдем x. Она является первообразной для скорости:
Подставляя в это уравнение значение t, получим:
Слайд 24Задача №3.
На поверхности Земли на широте φ лежит груз массой m.
Дано: φ, m, Rз. P - ? Fтр - ?
Решение:
x
y
φ
R
O
RЗ
В системе отсчета, связанной с Землей, на груз действует три обычные силы:
,
,
(эта сила препятствует скольжению груза от полюса к экватору).
Кроме того, действует центробежная сила инерции
= m
R,
где R = Rзcosφ – радиус окружности, по которой движется груз вместе с Землей.
Условия равновесия тела описывается уравнениями:
-mg + N + mω2Rзcos2φ = 0
-Fтр + mω2Rзsinφ cosφ = 0
Отсюда: P = N = mg - mω2Rзcos2φ = 0
Слайд 25Общий метод решения задач на колебательные движения.
Задача №1.
Ариометр массой m,
Дано: m, S, ρ. v - ?
Решение:
Возвращающей силой будет ΔFвыт, т.е. дополнительная выталкивающая сила, возникающая при погружении ариометра.
ΔFвыт = ρgΔV = ρgSΔh
k = ω02 = 2πν = ρgS
;
Слайд 26Задача №2.
На двух вращающихся в противоположные стороны валиках лежит горизонтальная доска.
Дано: m, μ, 2l. T - ?
Решение:
l - x
l + x
Если в начальный момент времени центр тяжести доски сместить от средней линии на некоторое расстояние x, то давление N1 и N2, а следовательно и силы трения и , не будут равны друг другу.
>
и, следовательно,
>
=
+
– возвращающая сила.
Слайд 27Задача №3.
Δm
x
x
В сообщающиеся сосуды U-образной формы налита ртуть. Её вывели из
Дано: m, ρ, d. T - ?
Решение:
Возвращающей силой в данной задаче является – дополнительная сила тяжести, возникающая в результате смещения ртути на высоту x.
Δm = ρΔV = ρSx
Δmg = ρSgx
k = ω02 = ρgS
S = πd2/4 – площадь сечения трубки.
k = ρgπd2/4
Слайд 28Задача №4.
mg∙cosα
α
x
Представьте себе, что в земном шаре по хорде прорыт
Дано: m, Rз, g=const. t - ?
Решение:
Тело в тоннеле будет совершать колебательное движение под действием возвращающей силы F = mg∙cosα.
cosα=x/R.
F = mgx/R
k = mg/R
Слайд 29Применение законов Кеплера.
Задача №1.
Земля
Солнце
а
Оцените время свободного падения тела с орбиты Земли
Дано: a, T. t - ?
Решение:
Падение тела с Земли на солнце Можно рассматривать как движение по очень сильно вытянутой узкой эллиптической орбите, касающейся Земли и Солнца. Большая ось такого эллипса равна расстоянию от Земли до Солнца. Используем III-ий закон Кеплера, сравнивая движение Земли вокруг Солнца с падением данного тела:
T2/T12 = a3/a13, где
а – расстояние от Земли до Солнца (большая полуось Земной орбиты),
а1 – большая полуось мнимой орбиты падающего тела, а1 = а/2,
Т – период обращения Земли вокруг Солнца,
Т1 – период обращения падающего тела по мнимой орбите.
Если Т = 365 суток, то t = 65 суток.
Слайд 30Задача №2.
На большом расстоянии от Земли метеорит движется относительно неё со
Дано: v0. lmax - ?
Решение:
На большом расстоянии от Земли, где потенциальную энергию взаимодействие с Землей можно считать равной нулю, метеорит имеет скорость v0 и его полная энергия равна кинетической mv02/2. Если бы начальная скорость метеорита v0 была равна
нулю, то, двигаясь только под действием силы притяжения Земли, он обязательно упал бы на Землю, двигаясь по прямой, и при падении имел у поверхности Земли скорость, равную второй космической vII = 11,2 км/с. Если начальная скорость метеорита отлична от нуля, то он в поле земного тяготения движется по гиперболе и будет захвачен Землей только тогда, когда эта гипербола «заденет» земной шар.
v0
Слайд 31При движении метеорита в поле тяжести Земли выполняется закон сохранения энергии:
(1)
,
Второй закон Кеплера о постоянстве секторной скорости справедлив и для разомкнутых траекторий.
(2) lv0 = Rv
Метеорит упадет на Землю только тогда, когда его прицельное расстояние l не превосходит радиуса земли.
Слайд 32Применение принципа симметрии для решения задач.
Задача №1.
Определить напряженность электрического поля
(1)
2q
q
3q
4q
Задача со скрытой симметрией. Модель ситуации можно представить как результат наложения симметричного расположения зарядов (2) и несимметричного (3):
(2)
q
q
q
q
(3)
q
2q
3q
(4)
q
q
(5)
2q
2q
Ситуация (3) – результат наложения двух симметричных ситуаций (4) и (5).
Слайд 33В ситуациях (2), (3), (4) напряженность поля в центре квадрата равна
По принципу суперпозиции полей:
2q
2q
a
1
2
Из соображений симметрии
Как видим из примера, решение задачи упрощается, если заметить симметрию.
Слайд 34Задача №2.
Поверхность полусферической чаши радиусом R с тонкими стенками заряжена с
Дано: R, σ. φ - ?
Решение:
A
R
q=σΔS
q’= σ’ΔS
Рассмотрим вспомогательную задачу: найдем потенциал φ0 поля, создаваемого равномерно заряженной сферой. Он одинаков во всех точках внутри сферы и равен
С другой стороны, по принципу суперпозиции он равен сумме потенциалов, создаваемых двумя полусферами. Из симметрии ясно, что потенциалы в любой точке интересующей нас поверхности, создаваемые верхней и нижней полусферами, равны. Поэтому потенциал, создаваемый одной полусферой, равен
Слайд 35Задача №3.
На расстоянии l от большого куска металла с плоской границей
q
l
Точечный заряд вблизи проводящей стенки.
Слева от стенки электрическое поле индуцированных на ней зарядов эквивалентно полю зарядов –q.
q
-q
Слайд 36Прежде всего ясно, что в толще металла электрического поля нет:
Т.к. на поверхности проводника индуцируются заряды, то полное поле слева представляет собой сумму полей заряда q и индуцированных зарядов. Равное нулю поле в правом полупространстве тоже можно рассматривать как сумму полей заряда q и индуцированных зарядов. Поэтому ясно, что поле справа от границы эквивалентно полю одного точечного заряда –q, помещенного в ту же точку, где находится заряд q. Но поле индуцированных зарядов симметрично относительно плоской границы металла. Поэтому слева от границы оно эквивалентно полю точечного заряда –q, расположенного справа от плоскости симметрично заряду q.
Итак, полное поле в левом полупространстве представляет собой суперпозицию полей, создаваемых зарядом q и зарядом –q, расположенном справа от плоскости симметрично заряду q.
Полученный результат можно кратко сформулировать так: действие плоской границы проводника с индуцированными на ней зарядами можно заменить действием точечного заряда –q, являющегося как бы зеркальным изображением данного заряда q в проводящей плоскости. Поэтому описанный способ нахождения поля носит название метода изображений.
Зная электрическое поле, можно рассчитать поверхностную плотность индуцированных на проводнике зарядов и силу, действующую на заряд q.
Слайд 37
q
-q
σ = E ε0
Заряд q притягивается к проводнику с такой же
Вычислим энергию взаимодействия заряда q с проводящей плоскостью. Эта энергия равна работе, которую нужно совершить, чтобы удалить заряд q на бесконечность. При удалении заряда q от поверхности металла будет удаляться и его изображение –q в противоположную сторону. Может
показаться, что совершенная при этом работа будет равна , но
это не верно, т.к. заряда –q на самом деле нет, и сила будет действовать только на один заряд. Следовательно, работа этой силы будет в два раза меньше:
Значит, искомая энергия равна
, знак «минус» соответствует энергии притяжения.
Слайд 38Задача №4.
Две звезды массами m1 и m2 образуют двойную систему с
Дано: m1, m2, R. T - ?
Решение:
m1
m2
r1
r2
R
Сумма расстояний звезд от общего центра масс r1 + r2 = R не изменяется. Используя принцип симметрии, будем рассматривать не движение звезд вокруг центра масс, а движение центра масс вокруг одной из звезд. В этой системе отсчета центр масс будет двигаться по окружности радиусом R.
Mц.м. = m1 + m2
G∙ = 4π2Rm/T2 T = 2 π √R3/G(m1 + m2)
Mц.м.∙m
R2
O