Автор: Михалкина О. К. учитель МОУ «СОШ №1 г. Ершова»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи на вероятность для подготовка к ОГЭ и ЕГЭ по математике
Содержание
- 1. Задачи на вероятность для подготовка к ОГЭ и ЕГЭ по математике
- 2. Профильный уровень ЕГЭ 2015 по математикеЕГЭ по
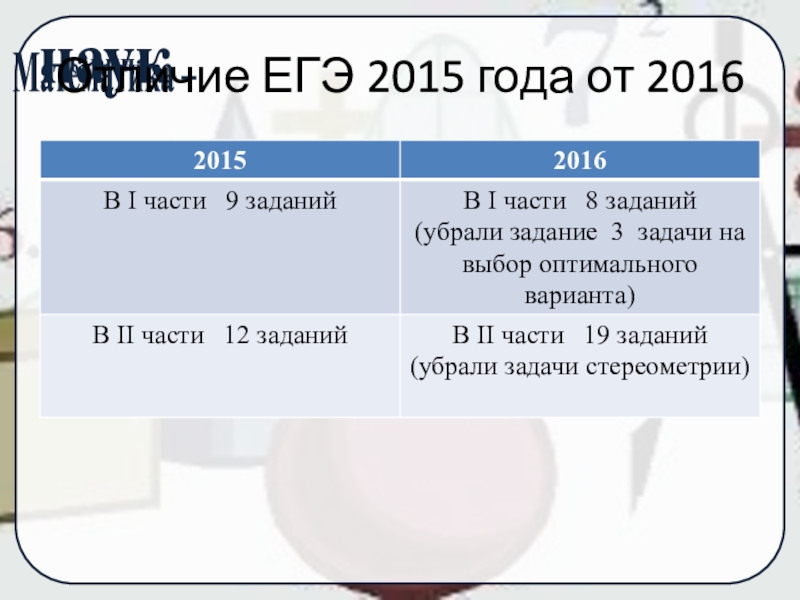
- 3. Отличие ЕГЭ 2015 года от 2016
- 4. Задача 1.
- 5. Задача 2В случайном эксперименте бросают три игральные
- 6. Задача 3В случайном эксперименте симметричную монету бросают
- 7. Задача 4Научная конференция проводится в 3 дня.
- 8. Задача 5Перед началом первого тура чемпионата по
- 9. Задача 6В чемпионате мира учувствуют 20 команд.
- 10. Задача 7На клавиатуре телефона 10 цифр, от
- 11. Задача 8Какова вероятность того, что случайно выбранное
- 12. Задача 9В классе 21 учащийся, среди них
- 13. Задача 10Вероятность того, что новый блендер в
- 14. Задача 11Механические часы с двенадцатичасовым циферблатом в
- 15. Задача 12На экзамене по геометрии школьнику достаётся
- 16. Значит, вероятность того, что на экзамене школьнику
- 17. Задача 13Две фабрики выпускают одинаковые стекла для
- 18. Произведением (или пересечением) нескольких событий называется событие,
- 19. Ситуация 2:Стекло оказывается со второй фабрики (вероятность
- 20. Задача 14В торговом центре два одинаковых автомата
- 21. P(A+B)=P(A)+P(B)-P(AB)P(A+B)=0,3+0,3-0,16=0,44Нас же интересует вероятность события, противоположного событию
- 22. Задача 15В магазине стоят два платёжных автомата.
- 23. Задача 16Биатлонист 5 раз стреляет по мишеням.
- 24. Задача 17Вероятность того, что новый пылесос прослужит
- 25. Задача 18Помещение освещается фонарём с тремя лампами.
- 26. Задача 19Вероятность того, что на тесте по
- 27. Задача 20В Волшебной стране бывает два типа
- 28. Используемые источники:1. http://egemaximum.ru/zadaniya-5-teoriya-veroyatnosti-chast-2/2. http://math.reshuege.ru/test?theme=1853. http://www.studfiles.ru/dir/cat32/subj1328/file14030/view149037.html4. https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%B2%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9
Профильный уровень ЕГЭ 2015 по математикеЕГЭ по математике профильного уровня состоит из двух частей, первая часть содержит задания с кратким ответом, вторая часть - задания с кратким и развернутым ответом.ЕГЭ профильного уровня создан на основе экзаменационной
Слайд 1Изменения в КИМах ЕГЭ по математике в 11 классах 2016 года.
Методика подготовки к ЕГЭ.
Слайд 2Профильный уровень ЕГЭ 2015 по математике
ЕГЭ по математике профильного уровня состоит
из двух частей, первая часть содержит задания с кратким ответом, вторая часть - задания с кратким и развернутым ответом.
ЕГЭ профильного уровня создан на основе экзаменационной модели госэкзамена 2014 года и проверят умения выполнять вычисления и преобразования, решать уравнения и неравенства, выполнять действия с функциями, с геометрическими фигурами, строить и исследовать математические модели.
ЕГЭ профильного уровня создан на основе экзаменационной модели госэкзамена 2014 года и проверят умения выполнять вычисления и преобразования, решать уравнения и неравенства, выполнять действия с функциями, с геометрическими фигурами, строить и исследовать математические модели.
Слайд 5Задача 2
В случайном эксперименте бросают три игральные кости. Найдите вероятность того,
что в сумме выпадет 7 очков. Результат округлите до сотых.
Решение:
В сумме выпадет 7 очков в следующих вариантах:
5+1+1 (3 комбинации)
1+2+4 (6 комбинаций)
1+3+3 (3 комбинации)
2+2+3 (3 комбинации)
Всего вариантов 3+6+3+3=15.
Каждый из трех кубиков может выпасть шестью гранями, поэтому общее число исходов равно6*6*6=216 .
Следовательно, вероятность того, что в сумме выпадет 7 очков, равна 15/216 =0,069…
Ответ: 0,07.
Решение:
В сумме выпадет 7 очков в следующих вариантах:
5+1+1 (3 комбинации)
1+2+4 (6 комбинаций)
1+3+3 (3 комбинации)
2+2+3 (3 комбинации)
Всего вариантов 3+6+3+3=15.
Каждый из трех кубиков может выпасть шестью гранями, поэтому общее число исходов равно6*6*6=216 .
Следовательно, вероятность того, что в сумме выпадет 7 очков, равна 15/216 =0,069…
Ответ: 0,07.
Слайд 6Задача 3
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того,
что решка не выпадет ни разу.
Решение:
Благоприятный исход: орел-орел-орел-орел.
Всего исходов – 2*2*2*2=16
Значит, вероятность того, что решка не выпадет ни разу – есть 1/16=0,0625
Ответ: 0,0625.
Решение:
Благоприятный исход: орел-орел-орел-орел.
Всего исходов – 2*2*2*2=16
Значит, вероятность того, что решка не выпадет ни разу – есть 1/16=0,0625
Ответ: 0,0625.
Слайд 7Задача 4
Научная конференция проводится в 3 дня. Всего запланировано 75 докладов — в
первый день 27 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение:
Всего запланировано 75 докладов, и так как в первый день запланировано 27, то на оставшиеся два дня остается 75-27=48 докладов, при этом во второй и третий дни будет прочитано по 48:2=24 доклада.
Значит вероятность, что доклад профессора М. окажется запланированным на третий день есть
Ответ: 0,32.
Решение:
Всего запланировано 75 докладов, и так как в первый день запланировано 27, то на оставшиеся два дня остается 75-27=48 докладов, при этом во второй и третий дни будет прочитано по 48:2=24 доклада.
Значит вероятность, что доклад профессора М. окажется запланированным на третий день есть
Ответ: 0,32.
Слайд 8Задача 5
Перед началом первого тура чемпионата по шашкам участников разбивают на
игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России?
Решение:
В первом туре Василий Лукин может сыграть с 26 − 1 = 25 шашистом, из которых 3 − 1 = 2 из России.
Значит, вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России, есть
Ответ: 0,08.
Решение:
В первом туре Василий Лукин может сыграть с 26 − 1 = 25 шашистом, из которых 3 − 1 = 2 из России.
Значит, вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России, есть
Ответ: 0,08.
Слайд 9Задача 6
В чемпионате мира учувствуют 20 команд. С помощью жребия их
нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Китая окажется в первой группе?
Решение:
Количество карточек с номером «1» – 4 штуки. Всего карточек (команд) – 20.
Значит, вероятность того, что команда Китая окажется в первой группе равна
Ответ: 0,2.
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Китая окажется в первой группе?
Решение:
Количество карточек с номером «1» – 4 штуки. Всего карточек (команд) – 20.
Значит, вероятность того, что команда Китая окажется в первой группе равна
Ответ: 0,2.
Слайд 10Задача 7
На клавиатуре телефона 10 цифр, от 0 до 9. Какова
вероятность того, что случайно нажатая цифра будет меньше 4?
Решение:
На клавиатуре телефона цифр меньше 4-х – 4 штуки (0; 1; 2; 3). Всего цифр 10.
Значит, вероятность того, что случайно нажатая цифра будет меньше 4 равна
Ответ: 0,4.
Решение:
На клавиатуре телефона цифр меньше 4-х – 4 штуки (0; 1; 2; 3). Всего цифр 10.
Значит, вероятность того, что случайно нажатая цифра будет меньше 4 равна
Ответ: 0,4.
Слайд 11Задача 8
Какова вероятность того, что случайно выбранное натуральное число от 41
до 56 делится на 2?
Решение:
От 41 до 56 ровно 16 чисел. Среди них четных 8 штук (42; 44; 46; 48; 50; 52; 54; 56).
Значит, вероятность того, что случайно выбранное натуральное число от 41 до 56 делится на 2 равна
Ответ: 0,5.
Решение:
От 41 до 56 ровно 16 чисел. Среди них четных 8 штук (42; 44; 46; 48; 50; 52; 54; 56).
Значит, вероятность того, что случайно выбранное натуральное число от 41 до 56 делится на 2 равна
Ответ: 0,5.
Слайд 12Задача 9
В классе 21 учащийся, среди них два друга — Вадим и
Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.
Решение:
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг окажется среди этих 6 человек, равна 6 : 20 = 0,3.
Ответ: 0,3.
Решение:
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг окажется среди этих 6 человек, равна 6 : 20 = 0,3.
Ответ: 0,3.
Слайд 13Задача 10
Вероятность того, что новый блендер в течение года поступит в
гарантийный ремонт, равна 0,096. В некотором городе из 1000 проданных блендеров в течение года в гарантийную мастерскую поступило 102 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение:
Частота события «гарантийный ремонт» составляет 102/1000=0,102
Вероятность же, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,096.
Разница между частотой события и вероятностью составляет 0,102-0,96
Ответ: 0,006.
Решение:
Частота события «гарантийный ремонт» составляет 102/1000=0,102
Вероятность же, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,096.
Разница между частотой события и вероятностью составляет 0,102-0,96
Ответ: 0,006.
Слайд 14Задача 11
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и
перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 6, но не дойдя до отметки 9 часов.
Решение:
На циферблате между 6 часами и 9 располагаются три часовых деления.
Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
Ответ: 0,25.
Решение:
На циферблате между 6 часами и 9 располагаются три часовых деления.
Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
Ответ: 0,25.
Слайд 15Задача 12
На экзамене по геометрии школьнику достаётся один вопрос из списка
экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
События «Достанется вопрос по теме Вписанные углы» и «Достанется вопрос по теме вписанная окружность» – несовместные.
(События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.)Значит, вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем равна сумме вероятностей (Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий
Решение:
События «Достанется вопрос по теме Вписанные углы» и «Достанется вопрос по теме вписанная окружность» – несовместные.
(События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.)Значит, вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем равна сумме вероятностей (Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий
Слайд 16Значит, вероятность того, что на экзамене школьнику достанется вопрос по одной
из этих двух тем равна сумме вероятностей : 0,35+0,2=0,55
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий: P(A+B)=P(a)+P(B)
Ответ: 0,55.
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий: P(A+B)=P(a)+P(B)
Ответ: 0,55.
Слайд 17Задача 13
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика
выпускает 70% этих стекол, вторая – 30%. Первая фабрика выпускает 1% бракованных стекол, а вторая – 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Ситуация 1:
Стекло оказывается с первой фабрики (вероятность события 0,7) и (умножение) оно бракованное (вероятность события 0,01).
То есть должны произойти оба события. На языке теории вероятностей это означает произведение вероятностей каждого из событий: 0,7*0,01=0,007
Решение:
Ситуация 1:
Стекло оказывается с первой фабрики (вероятность события 0,7) и (умножение) оно бракованное (вероятность события 0,01).
То есть должны произойти оба события. На языке теории вероятностей это означает произведение вероятностей каждого из событий: 0,7*0,01=0,007
Слайд 18Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении
всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей: P(A*B)=P(A)*P(B)
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей: P(A*B)=P(A)*P(B)
Слайд 19Ситуация 2:
Стекло оказывается со второй фабрики (вероятность события 0,3) и оно бракованное (вероятность
события 0,03): 0,3*0,03=0,009
Поскольку при покупке стекла мы оказываемся в ситуации 1 или (сумма) в ситуации 2, то по формуле суммы вероятностей несовместных событий получаем:
0,007+0,009=0,016
Ответ: 0,016.
Поскольку при покупке стекла мы оказываемся в ситуации 1 или (сумма) в ситуации 2, то по формуле суммы вероятностей несовместных событий получаем:
0,007+0,009=0,016
Ответ: 0,016.
Слайд 20Задача 14
В торговом центре два одинаковых автомата продают кофе. Вероятность того,
что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение:
Вероятность события А: «кофе закончится в первом автомате» P(A) равна 0,3.
Вероятность события В: «кофе закончится во втором автомате» P(B) равна 0,3.
Вероятность события АB: «кофе закончится в обоих автоматах» P(АB) равна 0,16.
Вероятность суммы двух совместных событий А+В, есть сумма их вероятностей без вероятности события АB:
Решение:
Вероятность события А: «кофе закончится в первом автомате» P(A) равна 0,3.
Вероятность события В: «кофе закончится во втором автомате» P(B) равна 0,3.
Вероятность события АB: «кофе закончится в обоих автоматах» P(АB) равна 0,16.
Вероятность суммы двух совместных событий А+В, есть сумма их вероятностей без вероятности события АB:
Слайд 21P(A+B)=P(A)+P(B)-P(AB)
P(A+B)=0,3+0,3-0,16=0,44
Нас же интересует вероятность события, противоположного событию А+В. Действительно, всего возможны
4 события, отвечают событию А+В: P=1-0,44=0,56
Ответ: 0,56.
Ответ: 0,56.
Слайд 22Задача 15
В магазине стоят два платёжных автомата. Каждый из них может
быть неисправен с вероятностью 0,12 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:
Оба автомата неисправны с вероятностью 0,12*0,12=0,0144
Хотя бы один автомат исправен (исправен + неисправен, неисправен + исправен, исправен + исправен)– это событие, противоположное событию «оба автомата неисправны», поэтому его вероятность есть 1-0,0144=0,9856
Ответ: 0,9856.
Решение:
Оба автомата неисправны с вероятностью 0,12*0,12=0,0144
Хотя бы один автомат исправен (исправен + неисправен, неисправен + исправен, исправен + исправен)– это событие, противоположное событию «оба автомата неисправны», поэтому его вероятность есть 1-0,0144=0,9856
Ответ: 0,9856.
Слайд 23Задача 16
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень
при одном выстреле равна 0,85. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение:
Биатлонист попадает в мишень первый раз и (умножение) второй, и третий: 0,85*0,85*0,85=0,614125
Так как вероятность попадания в цель –0,85 , то вероятность противоположного события, промаха, –1-0,85=0,15
Биатлонист промахнулся при четвертом выстреле и при пятом:0,15*0,15=0,0225
Тогда вероятность того, что биатлонист первые 3 раза попал в мишень, а (и!) последние два промахнулся такова: 0,614125*0,0225=0,0138….≈0,01
Ответ: 0,01.
Решение:
Биатлонист попадает в мишень первый раз и (умножение) второй, и третий: 0,85*0,85*0,85=0,614125
Так как вероятность попадания в цель –0,85 , то вероятность противоположного события, промаха, –1-0,85=0,15
Биатлонист промахнулся при четвертом выстреле и при пятом:0,15*0,15=0,0225
Тогда вероятность того, что биатлонист первые 3 раза попал в мишень, а (и!) последние два промахнулся такова: 0,614125*0,0225=0,0138….≈0,01
Ответ: 0,01.
Слайд 24Задача 17
Вероятность того, что новый пылесос прослужит больше года, равна 0,92.
Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решение:
Рассмотрим следующие события:
А – «пылесос прослужит больше года, но меньше 2»,
В – «пылесос прослужит больше 2-х лет»,
С – «пылесос прослужит больше года».
Событие С есть сумма совместных событий А и В, то есть
P(A+B)=P(A)+P(B)-P(AB)
Но P(AB)=0, так как не может одновременно произойти и А, и В.
Поэтому 0,92=P(A)+0,84
Откуда P(A)=0,08
Ответ: 0,08.
Решение:
Рассмотрим следующие события:
А – «пылесос прослужит больше года, но меньше 2»,
В – «пылесос прослужит больше 2-х лет»,
С – «пылесос прослужит больше года».
Событие С есть сумма совместных событий А и В, то есть
P(A+B)=P(A)+P(B)-P(AB)
Но P(AB)=0, так как не может одновременно произойти и А, и В.
Поэтому 0,92=P(A)+0,84
Откуда P(A)=0,08
Ответ: 0,08.
Слайд 25Задача 18
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы
в течение года равна 0,07. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Вероятность перегорания всех трех лампочек в течении года 0,7*0,7*0,7=0,000343
Тогда вероятность противоположного события – хотя бы одна лампа не перегорит – есть 1-0,00343=0,999657
Ответ: 0,999657.
Решение:
Вероятность перегорания всех трех лампочек в течении года 0,7*0,7*0,7=0,000343
Тогда вероятность противоположного события – хотя бы одна лампа не перегорит – есть 1-0,00343=0,999657
Ответ: 0,999657.
Слайд 26Задача 19
Вероятность того, что на тесте по математике учащийся У. верно
решит больше 12 задач, равна 0,78. Вероятность того, что У. верно решит больше 11 задач, равна 0,88. Найдите вероятность того, что У. верно решит ровно 12 задач.
Решение:
Пусть событие А: «учащийся верно решит 12 задач»,
событие В: «учащийся решит больше 12 задач»,
событие С: «учащийся решит больше 11 задач».
При этом вероятность события С есть сумма вероятностей событий А и В: P(C)=P(A)+P(B)
0,88=P(A)+0,78
P(A)=0,1– это и есть искомая вероятность.
Ответ: 0,1.
Решение:
Пусть событие А: «учащийся верно решит 12 задач»,
событие В: «учащийся решит больше 12 задач»,
событие С: «учащийся решит больше 11 задач».
При этом вероятность события С есть сумма вероятностей событий А и В: P(C)=P(A)+P(B)
0,88=P(A)+0,78
P(A)=0,1– это и есть искомая вероятность.
Ответ: 0,1.
Слайд 27Задача 20
В Волшебной стране бывает два типа погоды: хорошая и отличная,
причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 3 августа погода в Волшебной стране хорошая. Найдите вероятность того, что 6 августа в Волшебной стране будет отличная погода.
Решение:
Возможны следующие события (при условии, что 3 августа хорошая погода):
А) ХХХХ В) ХОХХ С) ХХОХ D) ХХХО E) ХООХ F) ХХОО J) ХООО H) ХОХО
(Мы отметили за «X» – «хорошая погода», «O» – «отличная погода»)
Интересующие нас события (6 августа – отличная погода): D, F, J, H.
Событие D: XХXO произойдет с вероятностью 0,8*0,8*0,2=0,128
Событие F: ХХОО произойдет с вероятностью 0,8*0,2*0,8=0,128
Событие J: ХOОО произойдет с вероятностью 0,2*0,8*0,8=0,128
Событие H: ХОXО произойдет с вероятностью 0,2*0,2*0,2=0,008
Тогда вероятность того, что 6 августа в Волшебной стране будет отличная погода есть 3*0,128+0,008=0,392
Ответ: 0,392.
Решение:
Возможны следующие события (при условии, что 3 августа хорошая погода):
А) ХХХХ В) ХОХХ С) ХХОХ D) ХХХО E) ХООХ F) ХХОО J) ХООО H) ХОХО
(Мы отметили за «X» – «хорошая погода», «O» – «отличная погода»)
Интересующие нас события (6 августа – отличная погода): D, F, J, H.
Событие D: XХXO произойдет с вероятностью 0,8*0,8*0,2=0,128
Событие F: ХХОО произойдет с вероятностью 0,8*0,2*0,8=0,128
Событие J: ХOОО произойдет с вероятностью 0,2*0,8*0,8=0,128
Событие H: ХОXО произойдет с вероятностью 0,2*0,2*0,2=0,008
Тогда вероятность того, что 6 августа в Волшебной стране будет отличная погода есть 3*0,128+0,008=0,392
Ответ: 0,392.