- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Введение в комбинаторику и теорию вероятностей
Содержание
- 1. Введение в комбинаторику и теорию вероятностей
- 2. Комбинаторика.«комбинаторика» происходит от латинского слова combinare –
- 3. Пример 2. Сколько трёхзначных чисел можно составить
- 4. Квадратные числа
- 5. Треугольные числа
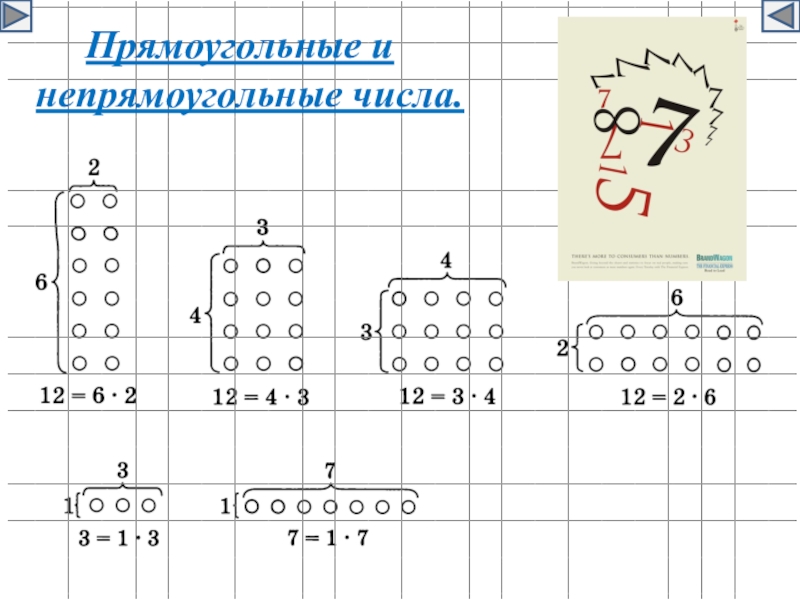
- 6. Прямоугольные и непрямоугольные числа.
- 7. Факториал.Таблица факториалов:Определение. Факториалом натурального числа n называется
- 8. Перестановки.Определение. Перестановкой называется конечное множество, в котором
- 9. Пример 1. Сколькими способами могут быть расставлены
- 10. Пример 2. Сколько различных четырёхзначных чисел можно
- 11. Пример 3. Имеется 10 различных книг, среди
- 12. Размещения.Определение. Размещением из n элементов, называютконечного множества по k, где упорядоченное множество, состоящее из kэлементов.
- 13. Пример 1. Из 12 учащихся нужно отобрать
- 14. Пример 2. Сколько существует семизначных телефонных номеров,
- 15. Пример 3. Сколько существует трёхзначных чисел, составленных
- 16. Сочетания.Определение. Подмножества, составленные из n элементов данного
- 17. Треугольник Паскаля 1 1
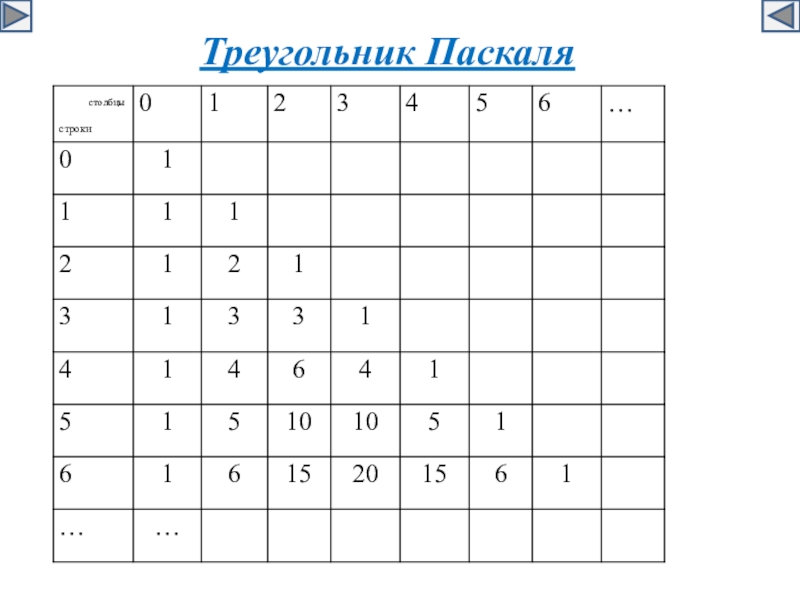
- 18. Треугольник Паскаля
- 19. Треугольник Паскаля…
- 20. Пример 1. Сколькими способами можно выбрать трёх дежурных из класса, в котором 20 человек?Решение:
- 21. Пример 2. Из вазы с цветами, в
- 22. Пример 3. Семь огурцов и три помидора
- 23. Частота и вероятность. Определение. Частотой случайного события в
- 24. Частота и вероятность. Определение. Вероятностью события А называется
- 25. Пример 1. В урне 10 одинаковых
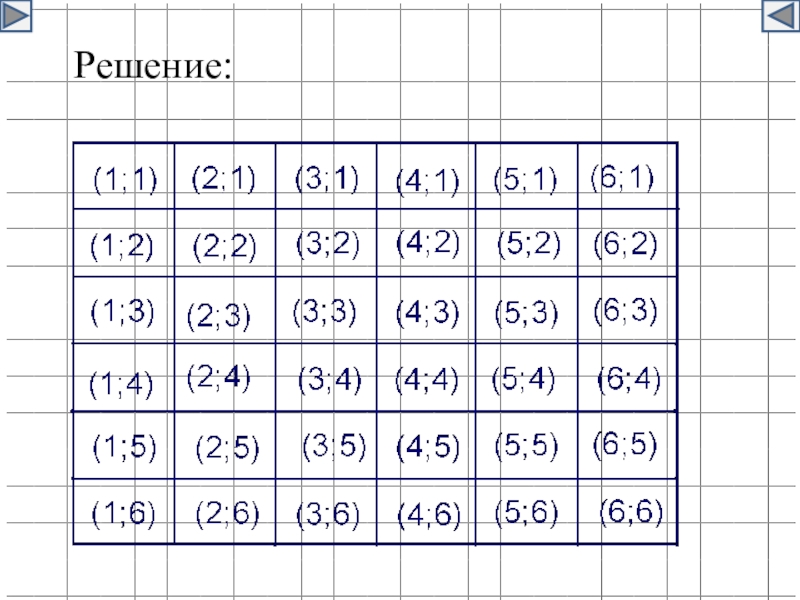
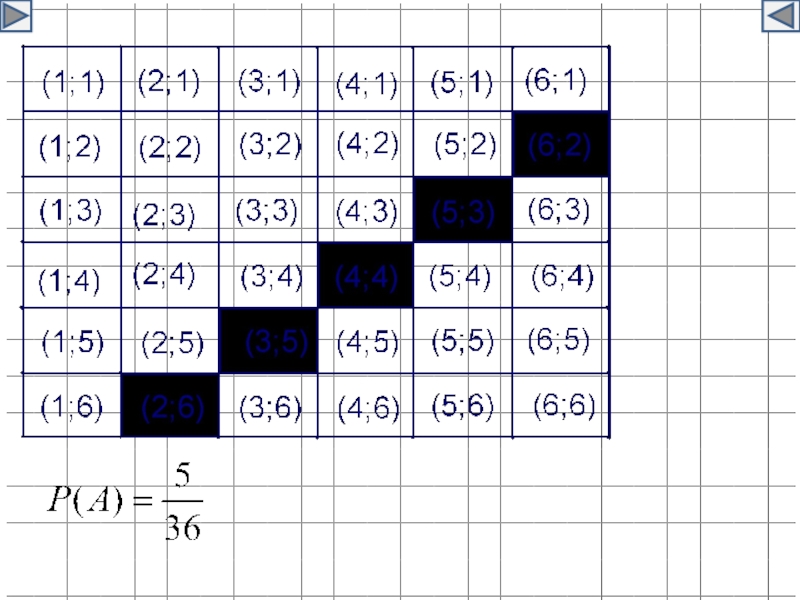
- 26. Пример 2. Коля и Миша бросают два
- 27. Решение:
- 28. Слайд 28
- 29. Слайд 29
- 30. Пример 3. Из собранных 10 велосипедов только
- 31. Сложение вероятностей.
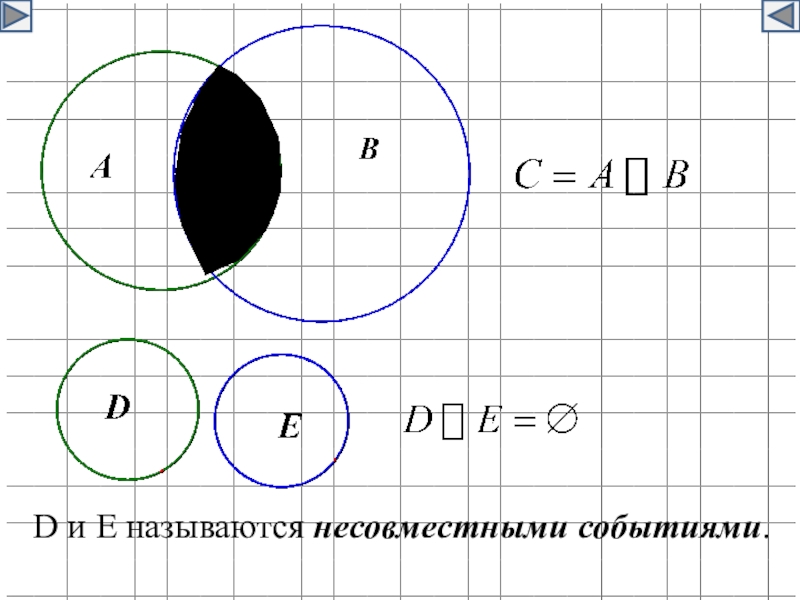
- 32. D и E называются несовместными событиями.
- 33. Сложение вероятностей.Вероятность наступления хотя бы одного из двух несовместных событий равна сумме их вероятностей.
- 34. Пример 1. В урне находятся 30 шаров
- 35. Пример 2. В контейнере 10 деталей, из
- 36. - благоприятные события для А- благоприятные события для В
- 37. Умножение вероятностей.Вероятность совместного появления двух независимых событий равна произведению их вероятностей.
- 38. Пример 1. Монету бросают 3 раза подряд. Какова вероятность, что решка выпадет все три раза.Решение:
- 39. Пример 2. Вероятность попадания
- 40. событие - промах 1-го орудия событие - промах 2-го орудия события и независимыесобытия А ипротивоположные
Слайд 1Введение
в комбинаторику и теорию вероятностей.
Комбинаторика
Факториал
Перестановки
Размещения
Сочетания
Сложение вероятностей
Умножение вероятностей
Слайд 2
Комбинаторика.
«комбинаторика» происходит от латинского слова combinare – «соединять, сочетать».
Определение. Комбинаторика –
Слайд 3
Пример 2. Сколько трёхзначных чисел можно составить из цифр 1, 3,
1
3
5
7
3
3
3
5
5
5
7
7
7
1
1
1
5
5
5
5
5
5
7
7
7
7
7
7
3
3
3
3
1
1
1
1
1
1
3
3
дерево вариантов
Слайд 7
Факториал.
Таблица факториалов:
Определение. Факториалом натурального числа n называется произведение всех натуральных чисел
Слайд 8
Перестановки.
Определение. Перестановкой называется конечное множество, в котором установлен порядок элементов.
Число всевозможных
Pn = n!
Слайд 9
Пример 1.
Сколькими способами могут быть расставлены восемь участниц финального забега
Решение: P8 = 8! = 40 320
Слайд 10
Пример 2.
Сколько различных четырёхзначных чисел можно составить из цифр 0,
Решение: Р4 – Р3 = 4! – 3! = 18.
Слайд 11
Пример 3.
Имеется 10 различных книг, среди которых есть трёхтомник одного
Решение:
Слайд 12
Размещения.
Определение. Размещением
из n элементов
, называют
конечного множества по k, где
упорядоченное множество, состоящее из k
элементов.
Слайд 13
Пример 1.
Из 12 учащихся нужно отобрать по одному человеку для
Решение:
Слайд 14
Пример 2.
Сколько существует семизначных телефонных номеров, в которых все цифры
Решение:
Слайд 15
Пример 3.
Сколько существует трёхзначных чисел, составленных из цифр 1, 2,
Решение:
Слайд 16
Сочетания.
Определение. Подмножества, составленные из n элементов данного множества и содержащие k
Слайд 20
Пример 1.
Сколькими способами можно выбрать трёх дежурных из класса, в
Решение:
Слайд 21
Пример 2.
Из вазы с цветами, в которой стоят 10 красных
Решение:
Слайд 22
Пример 3.
Семь огурцов и три помидора надо положить в два
Решение:
Слайд 23
Частота и вероятность.
Определение. Частотой случайного события в серии испытаний называется отношение
в которых это событие наступило (благоприятные испытания), к числу всех испытаний.
, где m – число испытаний с
благоприятным исходом,
n – число всех испытаний.
Нахождение частоты предполагает, чтобы испытание было проведено фактически.
Слайд 24
Частота и вероятность.
Определение. Вероятностью события А называется отношение числа благоприятных для
.
Нахождение вероятности не требует, чтобы испытание проводилось в действительности.
Слайд 25 Пример 1. В урне 10 одинаковых шаров разного
Решение:
а)
б)
в)
Слайд 26
Пример 2.
Коля и Миша бросают два игральных кубика. Они договорились,
Слайд 30
Пример 3.
Из собранных 10 велосипедов только 7 не
Решение:
Слайд 33
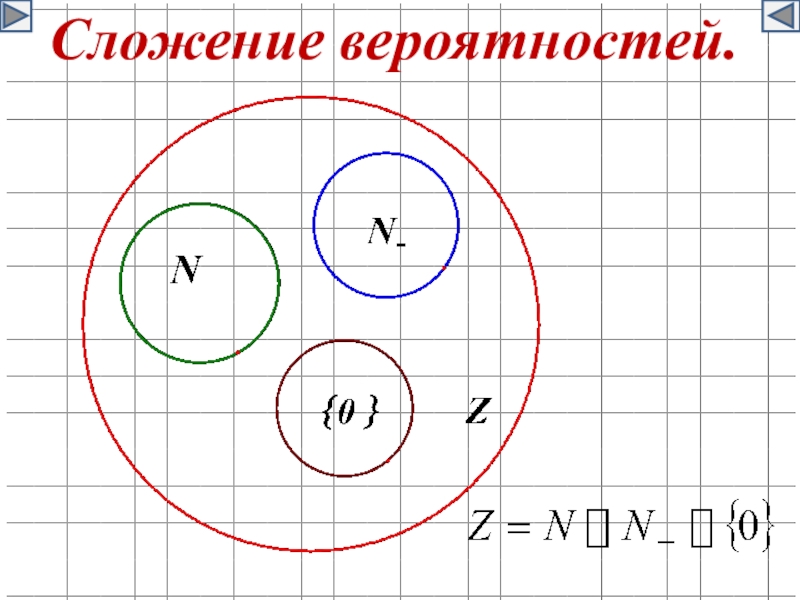
Сложение вероятностей.
Вероятность наступления хотя бы одного из двух несовместных событий равна
Слайд 34
Пример 1.
В урне находятся 30 шаров 10 белых, 15 красных
Решение:
Слайд 35
Пример 2.
В контейнере 10 деталей, из низ 2 нестандартные. Найдите
Решение:
- всего событий
Событие А – все 6 отобранных деталей стандартные,
событие В – среди 6 отобранных деталей одна
нестандартная.
Слайд 37
Умножение вероятностей.
Вероятность совместного появления двух независимых событий равна произведению их вероятностей.
Слайд 38
Пример 1.
Монету бросают 3 раза подряд. Какова вероятность, что решка
Решение:
Слайд 39
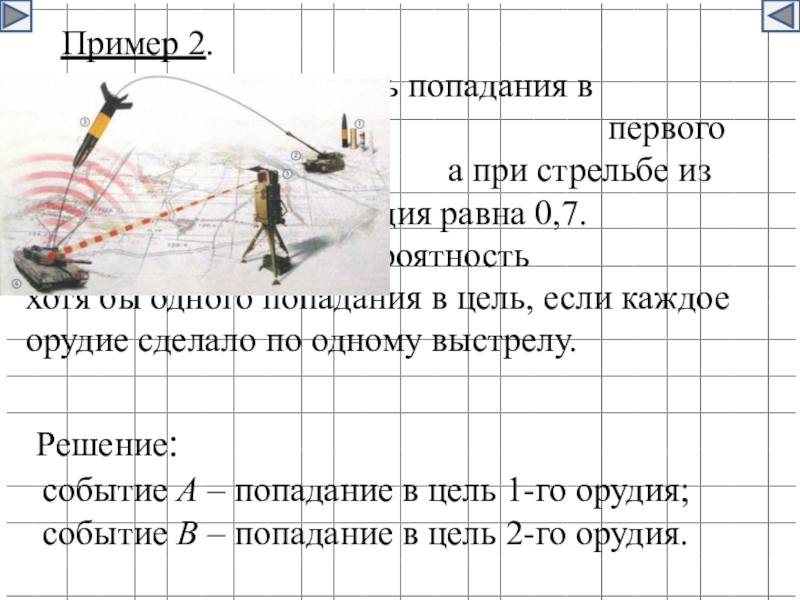
Пример 2.
Вероятность попадания в цель при
Найдите вероятность
хотя бы одного попадания в цель, если каждое
орудие сделало по одному выстрелу.
Решение:
событие А – попадание в цель 1-го орудия; событие В – попадание в цель 2-го орудия.
Слайд 40
событие
- промах 1-го орудия
событие
- промах 2-го
события
и
независимые
события А и
противоположные