Автор: Учитель математики высшей категории
МКОУ «Ободинская СОШ» Хабибова Патимат Магомедовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок-презентация по алгебре 8 класса Решение квадратных уравнений
Содержание
- 1. Урок-презентация по алгебре 8 класса Решение квадратных уравнений
- 2. «Математику уже затем учить надо, что она ум в порядок приводит»М.В. Ломоносов.
- 3. уравнение вида ах2 + вх +с =
- 4. ПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯНЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯКВАДРАТНЫЕ УРАВНЕНИЯа ≠
- 5. а) 7х2 – х + 5 =
- 6. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0 1.Перенос с
- 7. РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ :1 вариант:а)
- 8. Способы решения полных квадратных уравненийВыделение квадрата двучлена.Формула: D = b2- 4ac, x1,2=Теорема Виета.
- 9. РЕШИ УРАВНЕНИЯ способом выделения квадрата двучлена :1
- 10. Опр. Дискриминантом квадратного уравнения ах2 + bх
- 11. От чего зависит количество корней квадратного уравнения?
- 12. РЕШИМ УРАВНЕНИЯ с помощью формулы :Решить уравнение
- 13. Самостоятельная работа1 вариант5х2-4х—1=0х2-6х+9=02х2+2х+3=0–х2+3х+10=02 вариант3х2-5х+2=04х2-4х+1=06х2+3х+1=0–х2+2х+3=0
- 14. Ответы:
- 15. Теорема ВиетаСумма корней приведенного квадратного уравнения равна
- 16. Р.ДЕКАРТ1596-1650И. НЬЮТОН 1643-1727Ф. ВИЕТ1540 -1603
- 17. Исторические сведения:Квадратные уравнения впервые встречаются в работе
- 18. Неполные квадратные уравнения и частные виды полных
- 19. С какой пользой для вас прошёл этот
- 20. Учитель:- Спасибо, и наконец, поднимите руку кто
- 21. У вас на столе лежат листы с напечатанными индивидуальными заданиями. Решить уравненияДомашнее задание
- 22. СПАСИБО ЗА УРОК!
Слайд 1
АЛГЕБРА, 8 класс
Слайд 3
уравнение вида ах2 + вх +с = 0,
где х
а, в и с некоторые числа,
причем а 0.
ОПРЕДЕЛЕНИЕ:
Квадратным уравнением называется
Слайд 4
ПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
НЕПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в ≠ 0, с
а ≠ 0, в = 0, с = 0
5х2+3х-4=0
3х+х2-7=0
Х2-5х-6=0
36-12х+х2=0
8х2-3х=0
2х+х2=0
625+5х2=0
81х2-36=0
Слайд 5
а) 7х2 – х + 5 = 0
б) 22х - х2
в) 12 + 3х2 = 0
г) х – 9х2 = 0
д) - х + х2 = 1
а = 7, в = -1, с = 5;
а = -1, в = 22, с = 7;
а = 3, в = 0, с = 12
а = -9, в =1, с = 0;
а = 1, в =-1, с = 1
Определите коэффициенты
квадратного уравнения:
Слайд 6
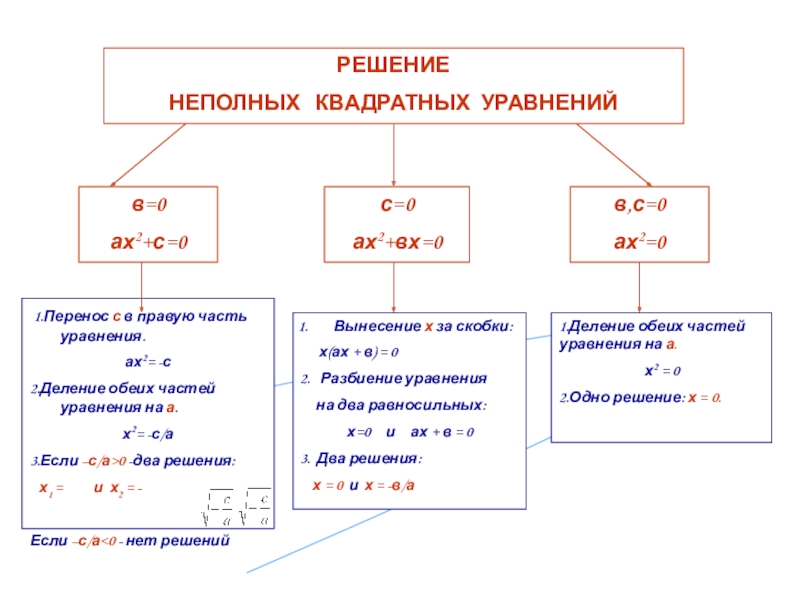
РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах2+с=0
с=0
ах2+вх=0
в,с=0
ах2=0
1.Перенос с в правую часть уравнения.
ах2=
2.Деление обеих частей уравнения на а.
х2= -с/а
3.Если –с/а>0 -два решения:
х1 = и х2 = -
Если –с/а<0 - нет решений
Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.
Слайд 7
РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ :
1 вариант:
а)
б) ( х + 1)2 + ( х -4)2 = 0
2 вариант:
а) 2х + х2= 0
б) 49х2 – 81 = 0
3 вариант:
а) 5х2 – 2х = 0
б) 288 + 2х2 = 0
Слайд 8
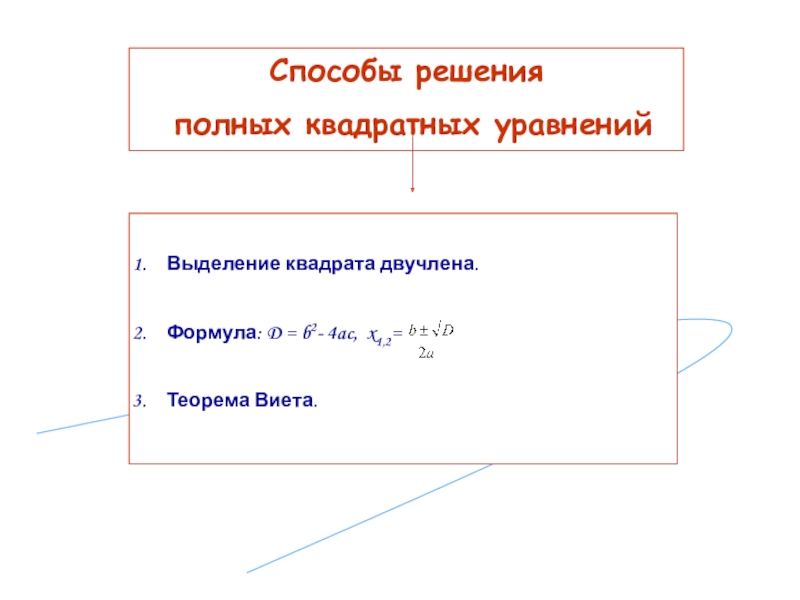
Способы решения
полных квадратных уравнений
Выделение квадрата двучлена.
Формула: D = b2- 4ac,
Теорема Виета.
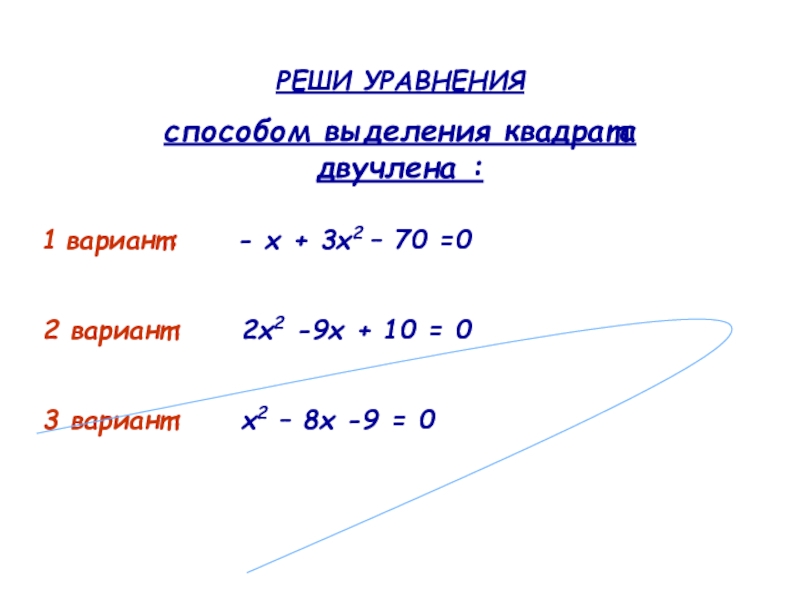
Слайд 9РЕШИ УРАВНЕНИЯ
способом выделения квадрата двучлена :
1 вариант: -
2 вариант: 2х2 -9х + 10 = 0
3 вариант: х2 – 8х -9 = 0
Слайд 10Опр. Дискриминантом квадратного уравнения ах2 + bх + с = 0
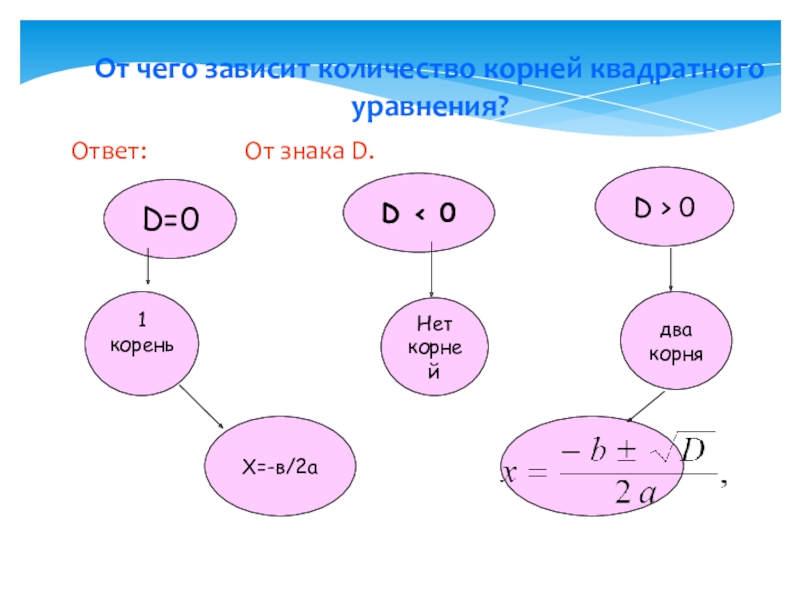
Возможны три случая:
D > 0
D = 0
D < 0
Дискриминант квадратного уравнения
Слайд 12РЕШИМ УРАВНЕНИЯ
с помощью формулы :
Решить уравнение 2x2- 5x + 2 = 0
Здесь a = 2, b = -5, c = 2.
Имеем D = b2- 4ac = (-5)2- 4⋅2⋅2 = 9.
Так как D > 0, то уравнение имеет два корня. Найдем их по формуле
то есть x1 = 2 и x2 = 0,5 - корни заданного уравнения.
Слайд 13Самостоятельная работа
1 вариант
5х2-4х—1=0
х2-6х+9=0
2х2+2х+3=0
–х2+3х+10=0
2 вариант
3х2-5х+2=0
4х2-4х+1=0
6х2+3х+1=0
–х2+2х+3=0
Слайд 15Теорема Виета
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с
х2+px+g=0- приведенное квадратное уравнение.
П о теореме Виета: х1 + х2= -p
х1* х2= g
Слайд 17Исторические сведения:
Квадратные уравнения впервые встречаются в работе индийского математика и астронома
Другой индийский ученый Брахмагупта (VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.
В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную форму.
Слайд 18Неполные квадратные уравнения и частные виды полных уравнений (х2 – х = а)
Слайд 19С какой пользой для вас прошёл этот урок, можно начать свой
Я знаю, что ...
Я хорошо знаю, что ...
Я должен знать, что …
Рефлексия
Слайд 20Учитель:
- Спасибо, и наконец, поднимите руку кто свою работу на уроке
-
- кто оценивает на “4”,
- кто оценивает свою работу на “3”.
Дети поднимают руки и учитель их оценивает, учитывая их мнение тоже.
Подведение итогов урока
Слайд 21У вас на столе лежат листы с напечатанными индивидуальными заданиями. Решить
Домашнее задание