- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок по тригонометрии Тригонометрический лабиринт
Содержание
- 1. Урок по тригонометрии Тригонометрический лабиринт
- 2. Из истории математикиЗарождение тригонометрии относится к глубокой
- 3. В 15- 17 веках над тригонометрией работали
- 4. В России первые тригонометрические таблицы были изданы
- 5. Эйлер стал рассматривать значения тригонометрических функций как
- 6. Легенда об Эйлере
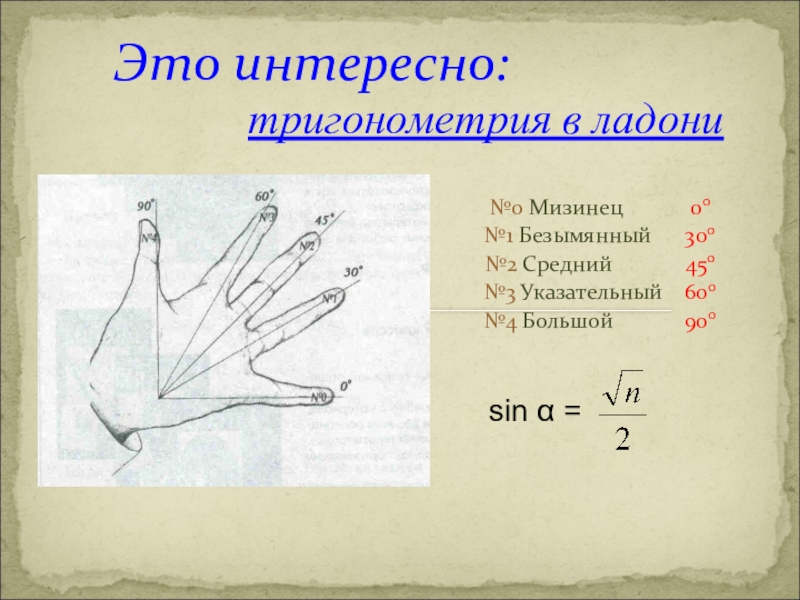
- 7. тригонометрия в ладониЭто интересно:№0 Мизинец 00№1 Безымянный 300№2 Средний 450№3 Указательный 600№4 Большой 900
Слайд 2Из истории математики
Зарождение тригонометрии относится к глубокой древности.
Одним из основоположников
2 в. до нашей эры
Важный вклад в развитие тригонометрии был внесен индийской математикой в период 5 - 12 век нашей эры.
Слайд 3В 15- 17 веках над тригонометрией работали такие крупнейшие ученые -
Из истории математики
Николай Коперник (1473-1543) –польский учёный
Иоганн Кеплер (1571-1630) –немецкий учёный
Франсуа Виет (1540-1603)-французский учёный
Слайд 4В России первые тригонометрические таблицы были изданы в 1703 году при
Из истории математики
Современный вид тригонометрия получила в
трудах великого ученого, члена Российской
академии наук Леонарда Эйлера (1707-1783).
На основании работ Л. Эйлера были составлены
учебники тригонометрии.
Построение теории тригонометрических
функций, начатое Эйлером, получило
завершение в трудах великого русского
ученого Н.И. Лобачевского.
Слайд 5Эйлер стал рассматривать значения тригонометрических функций как числа - величины тригонометрических
Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразное обозначение: sin а, cos а, tg а, ctg а.
(1707-1783)