- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок изучения нового материала по теме Логарифмы. 10 класс
Содержание
- 1. Урок изучения нового материала по теме Логарифмы. 10 класс
- 2. «Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней словно удваивает жизнь астрономов»П.С. Лаплас
- 3. Цель урокаПознакомиться с понятием логарифма, основным логарифмическим тождеством; научиться применять их на практике
- 4. Невозможно изучить новое без повторенияуже изученного
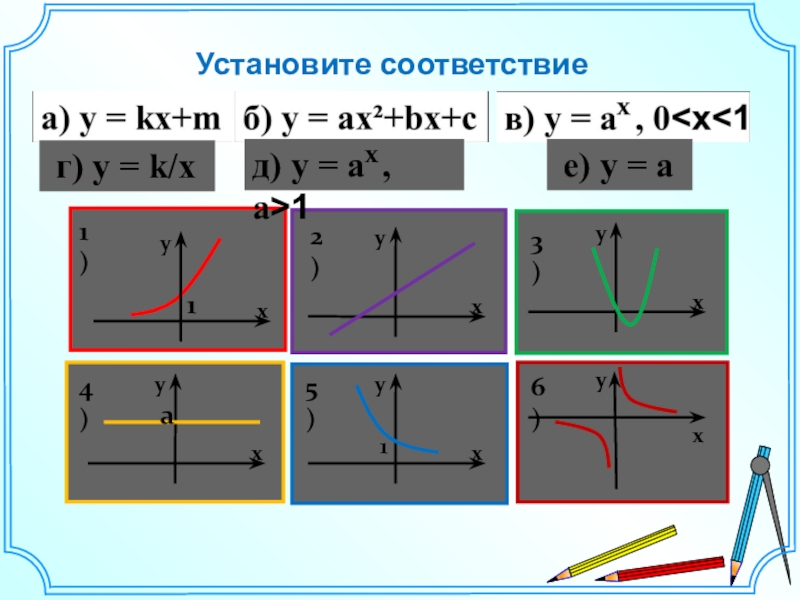
- 5. Установите соответствие г) y = k/x е) y = a
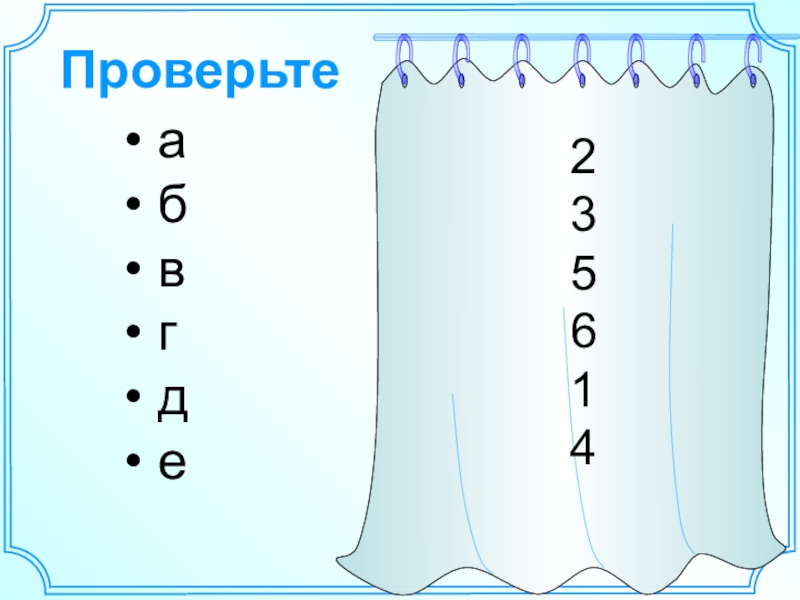
- 6. Проверьте235614 а б в г д е
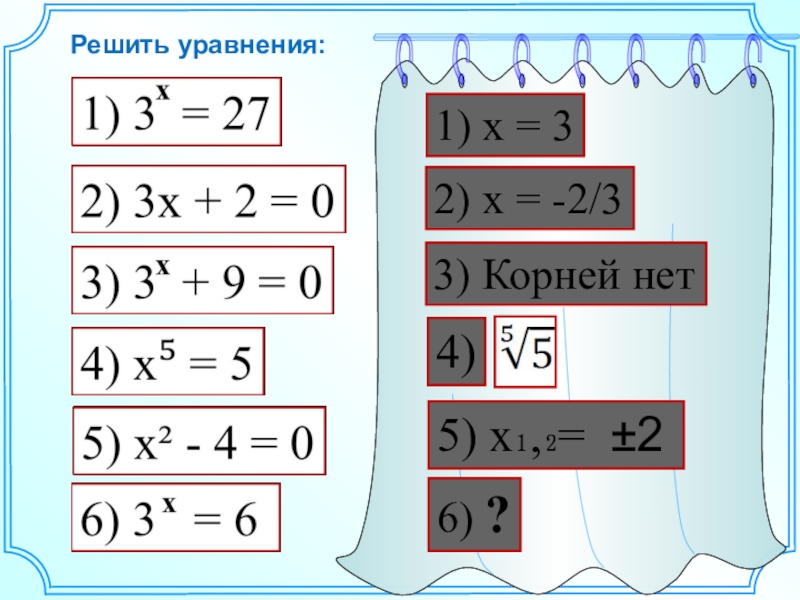
- 7. Решить уравнения:1) x = 32) x = -2/33) Корней нет5) x₁‚₂= ±26) ?
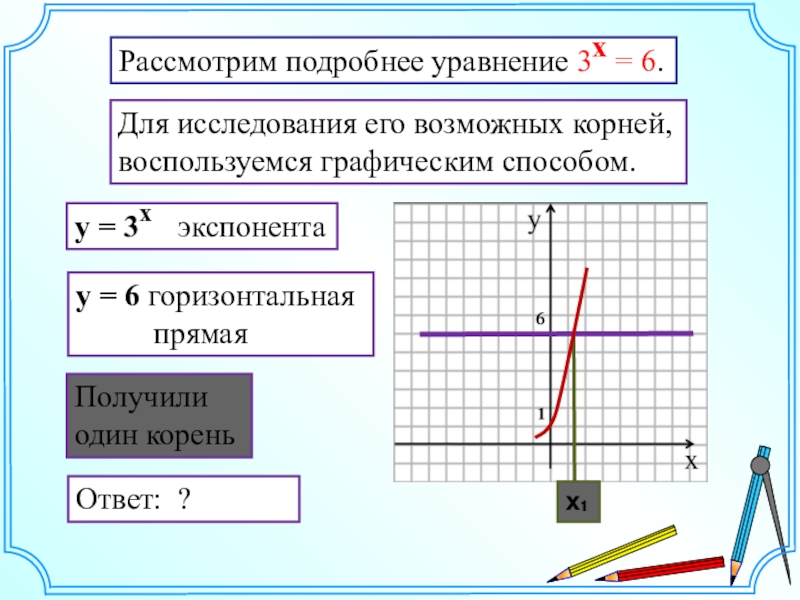
- 8. Для исследования его возможных корней,воспользуемся графическим способом.y
- 9. Решая последнее уравнение,мы столкнулись с проблемойзаписи полученного ответа.Прежних знаний для этогоявно недостаточно.
- 10. Выводы: уравнение имеет один корень корень –
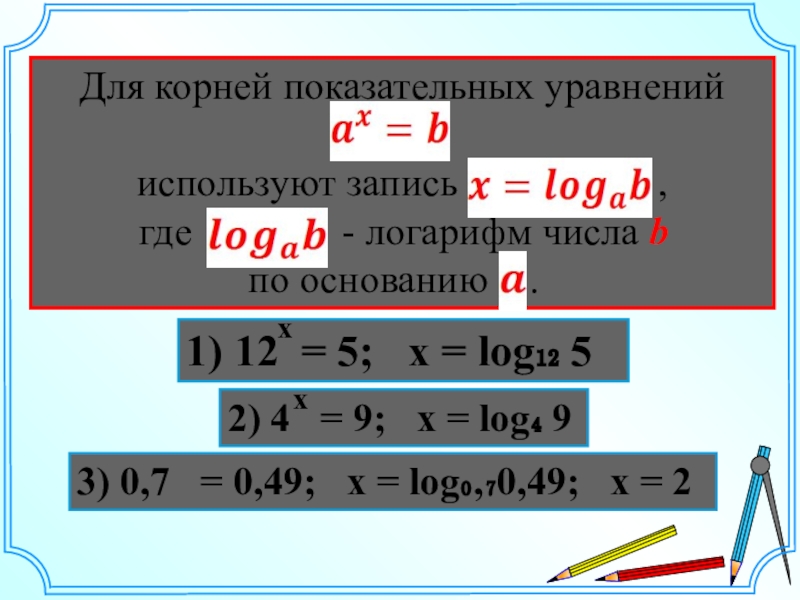
- 11. 1) 12 = 5; x =
- 12. Мы получили новую математическуюмодель – логарифм числа.Логарифмом
- 13. Вывод: значение логарифма –
- 14. Из определения логарифма следует:Основное логарифмическое тождество
- 15. Из определения логарифма следует:
- 16. Взаимно обратные действия: Возведение в степеньЛогарифмирование
- 17. Историческая справка На протяжении 16 века
- 18. Историческая справкаЛогарифмы были придуманы для ускорения и
- 19. Ценность логарифмовсостоит в сведении сложных действий возведения
- 20. Слайд 20
- 21. Вычислите№267-270(нечетные)
- 22. Вычислите№274-276(нечетные)
- 23. Выясните при каких значениях x существует логарифм№ 278(нечетные)Нет таких х
- 24. Оказываетсяматематическим символом соотношения формы и роста является логарифмическая спиральраковина моллюскарога горных барановсемена подсолнечника
- 25. ОказываетсяПо логарифмическим спиралям закручены и многие галактики, в том числе и Галактика, которой принадлежит Солнечная система
- 26. Ответьте на вопросы1. Где встречается понятие логарифма?2.
- 27. Домашнее задание1. Параграф 15 – выучить определение
«Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней словно удваивает жизнь астрономов»П.С. Лаплас
Слайд 2«Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней словно
удваивает жизнь астрономов»
П.С. Лаплас
П.С. Лаплас
Слайд 3Цель урока
Познакомиться с понятием логарифма,
основным логарифмическим тождеством;
научиться применять их
на практике
Слайд 8Для исследования его возможных корней,
воспользуемся графическим способом.
y = 3
экспонента
x
y = 6 горизонтальная
прямая
Ответ: ?
x₁
6
Получили
один корень
Слайд 9Решая последнее уравнение,
мы столкнулись с проблемой
записи полученного ответа.
Прежних знаний для этого
явно
недостаточно.
Слайд 10Выводы:
уравнение имеет один корень
корень – число
(показатель степени
числа 3)
Такой вывод можно сделать для
любого уравнения вида ,
где ,
Слайд 12Мы получили новую математическую
модель – логарифм числа.
Логарифмом числа по
основанию
называется такой показатель степени k,
в который надо возвести , чтобы
получить , т.е. log b = k,
Примеры: log₂16 = 4, т.к. 2⁴ = 16.
log₀‚₃0,09 =2, т.к. 0,3²=0,09
называется такой показатель степени k,
в который надо возвести , чтобы
получить , т.е. log b = k,
Примеры: log₂16 = 4, т.к. 2⁴ = 16.
log₀‚₃0,09 =2, т.к. 0,3²=0,09
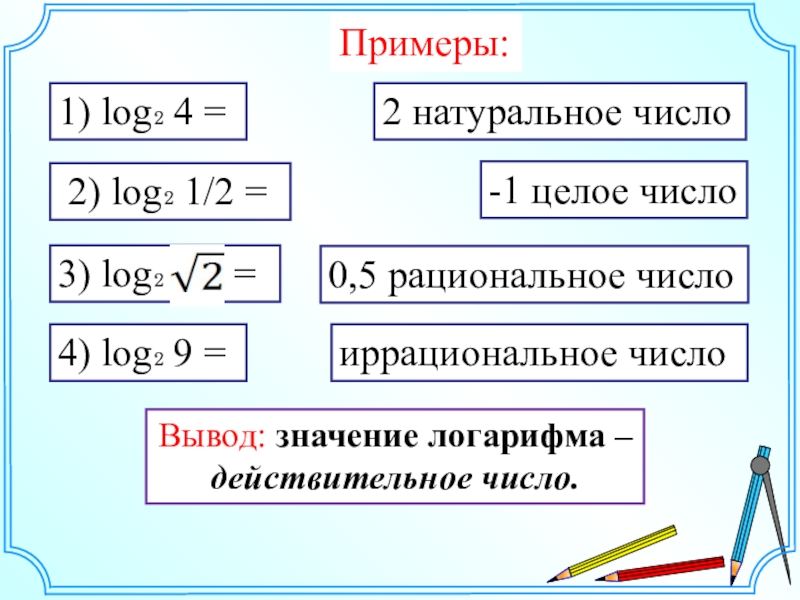
Слайд 13Вывод: значение логарифма – действительное
число.
Примеры:
1) log₂ 4 =
2) log₂ 1/2 =
4) log₂ 9 =
2 натуральное число
-1 целое число
0,5 рациональное число
иррациональное число
Слайд 17Историческая справка
На протяжении 16 века быстро возрастало количество приближенных
вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономам грозила реальная опасность утонуть в невыполненных расчетах.
Проблемы возникали и в других областях, например, в финансовом и страховом деле нужны были таблицы сложных процентов для различных значений процента.
Главную трудность представляли умножение, деление многозначных чисел.
Проблемы возникали и в других областях, например, в финансовом и страховом деле нужны были таблицы сложных процентов для различных значений процента.
Главную трудность представляли умножение, деление многозначных чисел.
Слайд 18Историческая справка
Логарифмы были придуманы для ускорения и упрощения вычислений.
Идея логарифма, т. е.
идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития.
Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632).
Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632).
Джон Непер
В1614г. была опубликована работа Непера под названием «Описание удивительной таблицы логарифмов»
Слово «логарифм» введено Непером, происходит от греческих слов logoz и ariumoz - оно означает буквально “числа отношений”.
Слайд 19Ценность логарифмов
состоит в сведении сложных действий возведения в степень и извлечения
корня к более простым действиям - умножению и делению, а последних к - самым простым – сложению и вычитанию.
Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов упростило жизнь тех, кто по роду своей деятельности был связан с громоздкими вычислениями и сложными расчетами.
Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов упростило жизнь тех, кто по роду своей деятельности был связан с громоздкими вычислениями и сложными расчетами.
Палочки Непера
Логарифмическая линейка
Слайд 24Оказывается
математическим символом соотношения формы и роста является логарифмическая спираль
раковина моллюска
рога горных
баранов
семена подсолнечника
Слайд 25Оказывается
По логарифмическим спиралям закручены и многие галактики, в том числе и
Галактика, которой принадлежит Солнечная система
Слайд 26Ответьте на вопросы
1. Где встречается понятие логарифма?
2. Для чего нужен логарифм
числа в математике?
3. Действие нахождения логарифма числа называют…
4. Чему равно основание данного
логарифма?
5.Каким числом может быть логарифм?
3. Действие нахождения логарифма числа называют…
4. Чему равно основание данного
логарифма?
5.Каким числом может быть логарифм?
Слайд 27Домашнее задание
1. Параграф 15 – выучить определение логарифма.
2. Решить в тетрадях
для домашних работ:
- первый уровень - №271-273(четные), №283(2).
- второй уровень - №279-281(четные), №284(четные).
- первый уровень - №271-273(четные), №283(2).
- второй уровень - №279-281(четные), №284(четные).
