задачи
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Урок одной задачи (11 класс)
Содержание
- 1. Презентация по математике Урок одной задачи (11 класс)
- 2. Повторить некоторые разделы курса математики2. Решить задачу из второго раздела контрольно измерительных материалов ЕГЭ
- 3. Каким свойством обладают отрезки касательных проведённых к
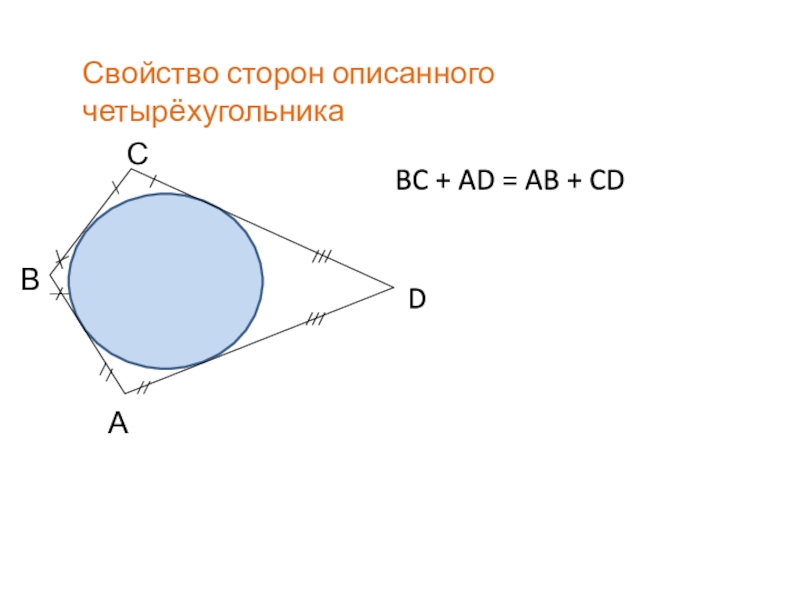
- 4. Свойство сторон описанного четырёхугольникаАВСDBC + AD = AB + CD
- 5. Формулы площадей фигур:Площадь треугольника:Площадь трапеции:bahaABCbch
- 6. Дать определение синуса и косинуса острого угла
- 7. Сформулируйте теорему синусовПовторим некоторые тригонометрические формулыСтороны треугольника пропорциональны синусам противоположных угловАВСсab
- 8. Задача: Окружность вписана в равнобокую трапецию.
- 9. O Окружность вписана в равнобокую трапецию.
- 10. OАВСKNMBM высота трапецииИз треугольника АВМ ВМ2=АВ2-АМ2=25-9=16
- 11. OАВСKNMDТНашли: SABCD=20 ;
Повторить некоторые разделы курса математики2. Решить задачу из второго раздела контрольно измерительных материалов ЕГЭ
Слайд 1Учитель: Милюхина Ольга Ивановна
МКОУ Лугавская СОШ №19
Красноярский край
Минусинский район
Урок одной
Слайд 2
Повторить некоторые разделы курса математики
2. Решить задачу из второго раздела контрольно
измерительных материалов ЕГЭ
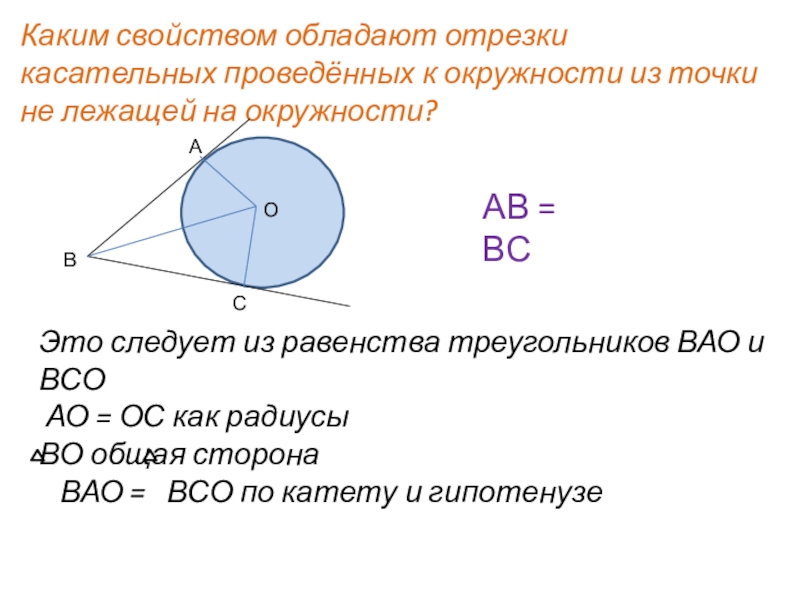
Слайд 3Каким свойством обладают отрезки касательных проведённых к окружности из точки не
лежащей на окружности?
А
В
С
О
АВ = ВС
Это следует из равенства треугольников ВАО и ВСО
АО = ОС как радиусы
ВО общая сторона
ВАО = ВСО по катету и гипотенузе
Слайд 6Дать определение синуса и косинуса острого угла в прямоугольном треугольнике
Синус острого
угла в прямоугольном треугольнике, это отношение противолежащего катета к гипотенузе
А
В
С
b
c
a
Косинус острого угла в прямоугольном треугольнике, это отношение прилежащего катета к гипотенузе
Слайд 7Сформулируйте теорему синусов
Повторим некоторые тригонометрические формулы
Стороны треугольника пропорциональны синусам противоположных углов
А
В
С
с
a
b
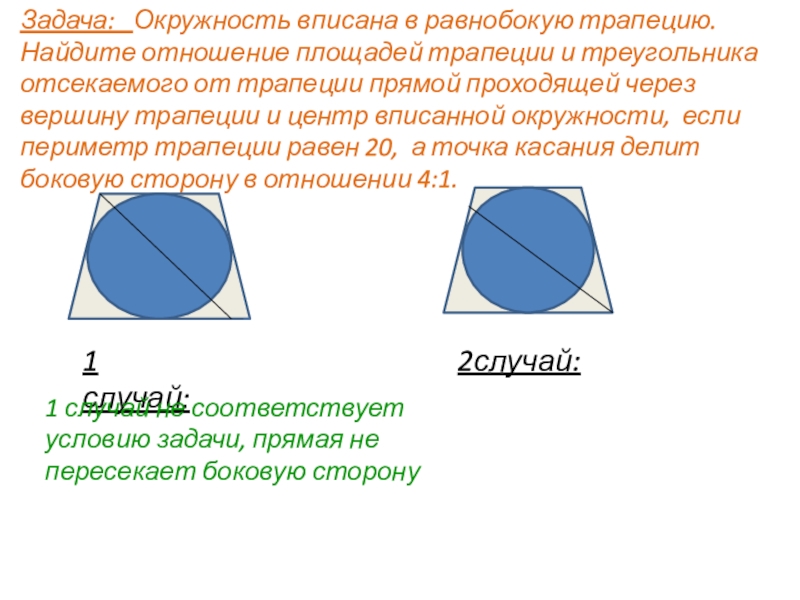
Слайд 8Задача: Окружность вписана в равнобокую трапецию. Найдите отношение площадей трапеции
и треугольника отсекаемого от трапеции прямой проходящей через вершину трапеции и центр вписанной окружности, если периметр трапеции равен 20, а точка касания делит боковую сторону в отношении 4:1.
1 случай:
2случай:
1 случай не соответствует условию задачи, прямая не пересекает боковую сторону
Слайд 9O
Окружность вписана в равнобокую трапецию. Найдите отношение площадей трапеции
и треугольника отсекаемого от трапеции прямой проходящей через вершину трапеции и центр вписанной окружности, если периметр трапеции равен 20, а точка касания делит боковую сторону в отношении 4:1.
А
В
С
D
K
N
Следовательно КВ=1, АК=4, АВ=5.
По условию АК:КВ=4:1
значит АВ содержит 5 частей
В описанном четырёхугольнике суммы противоположных сторон равны. АВ+СD=АD+ВС = 10 частей
Сумма всех сторон трапеции 20 частей и периметр 20 единиц, значит на каждую часть приходится 1 единица.
Отрезки касательных до точки касания равны, значит ВС=2, а АD=8.
Слайд 10O
А
В
С
K
N
M
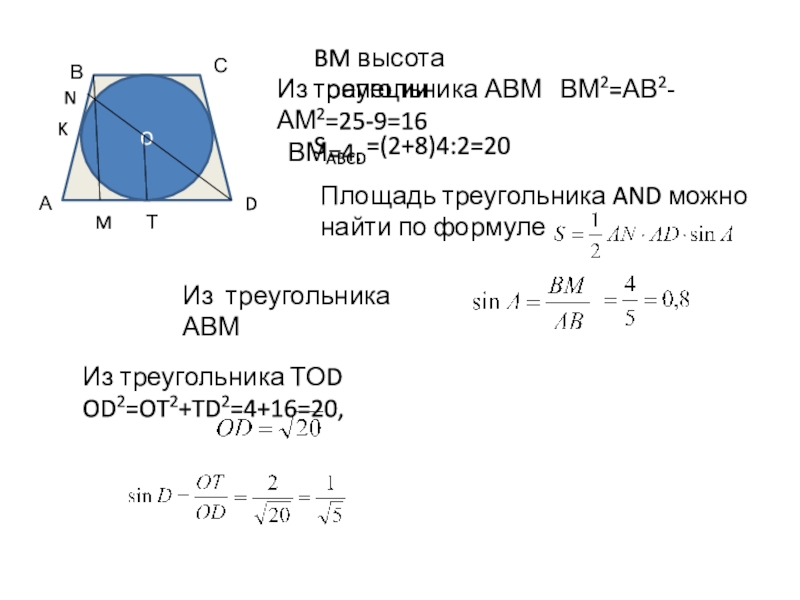
BM высота трапеции
Из треугольника АВМ ВМ2=АВ2-АМ2=25-9=16
ВМ=4.
SABCD=(2+8)4:2=20
Из треугольника АВМ
D
Площадь
треугольника AND можно найти по формуле
Т
Из треугольника ТОD OD2=OT2+TD2=4+16=20,
