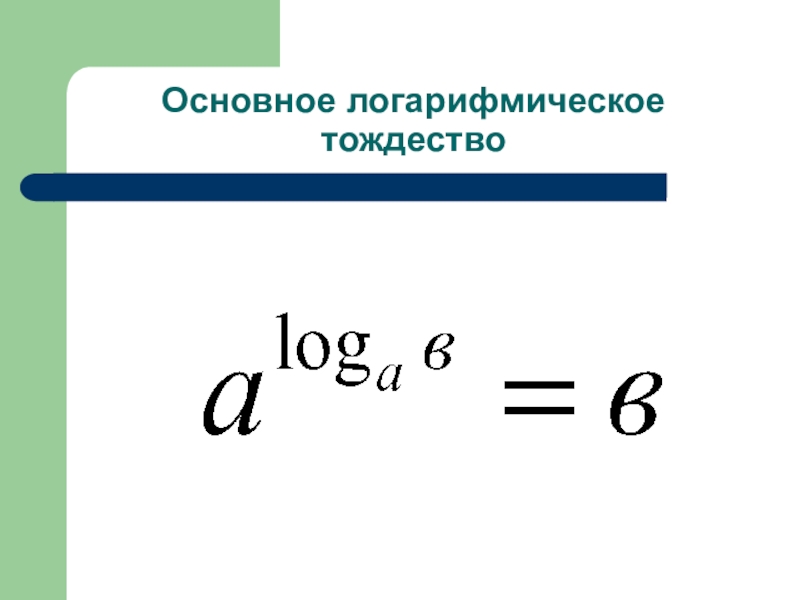учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Свойства логарифмов
Содержание
- 1. Презентация по алгебре на тему Свойства логарифмов
- 2. ПОНЯТИЕ ЛОГАРИФМА« Три пути ведут к знанию:
- 3. 1. Сформировать: знание определения логарифм
- 4. Методы и организационные формы: 1.Индивидуальная работа;2.Работа в
- 5. Определение логарифмаЛогарифмом числа в>0 по основанию а>0
- 6. Основное логарифмическое тождество
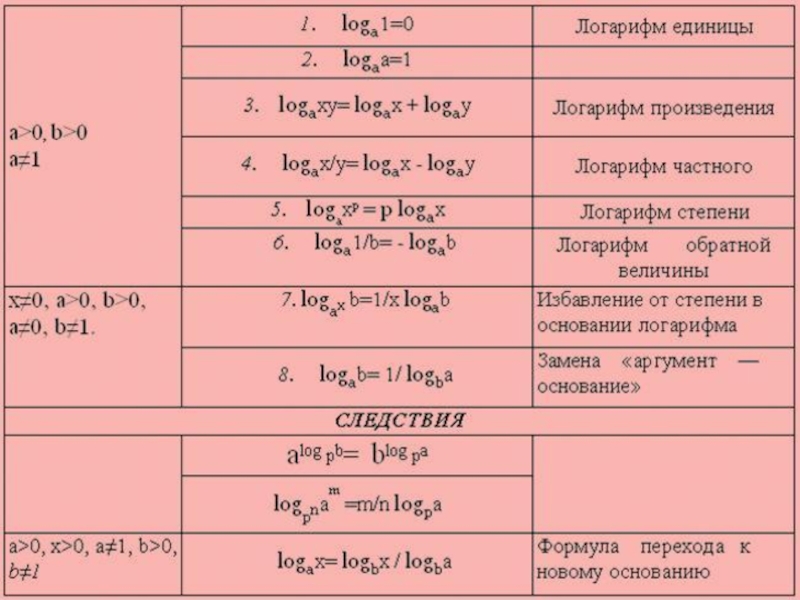
- 7. Свойства логарифмовЛогарифм произведения положительных чисел равен сумме логарифмов сомножителей:
- 8. Свойства логарифмовЛогарифм частного положительных чисел равен разности логарифмов делимого и делителя:
- 9. Свойства логарифмовЛогарифм степени положительного основания равен произведению показателя степени на логарифм основания степени:
- 10. Свойства монотонности логарифмовЕсли a>1 и
- 11. Свойства монотонности логарифмовЕсли 0 < а
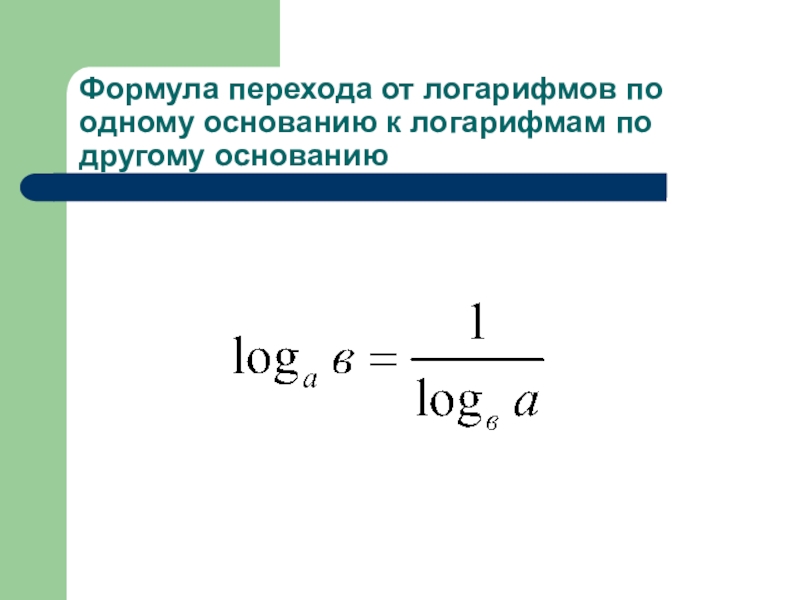
- 12. Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию
- 13. Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию
- 14. Десятичные логарифмыЕсли основание логарифма равно 10, то логарифм называется десятичным:
- 15. Десятичные логарифмы чисел, выраженных единицей с последующими нулями:
- 16. Десятичные логарифмы чисел, выраженных единицей с предшествующими нулями
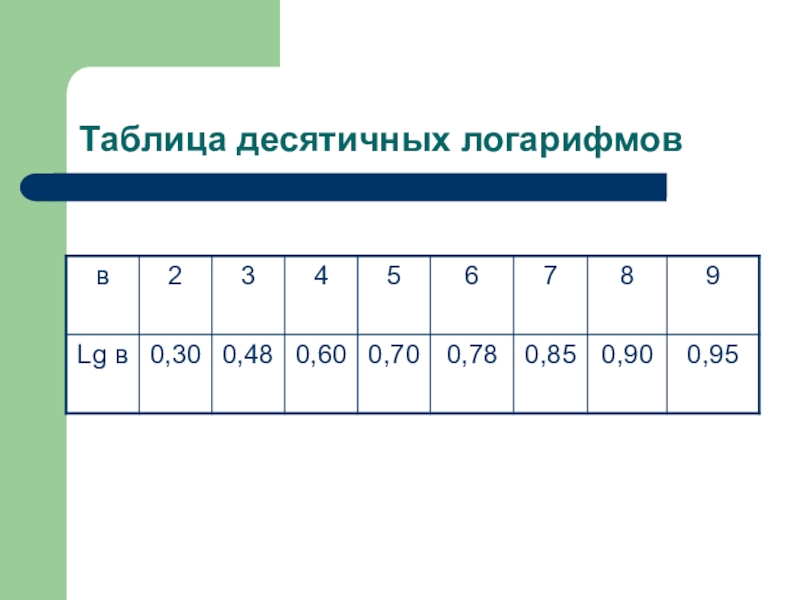
- 17. Таблица десятичных логарифмов
- 18. Натуральные логарифмыЕсли основание логарифма е 2,7, то логарифм называется натуральным:
- 19. Натуральные логарифмы
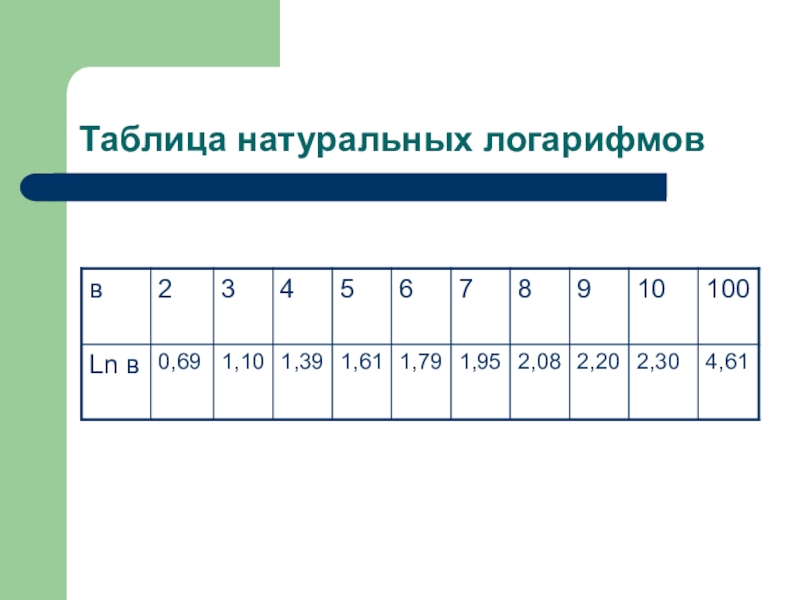
- 20. Таблица натуральных логарифмов
- 21. Логарифмирование алгебраических выраженийЕсли число х представлено
- 22. Прологарифмировать алгебраическое выражение:Пример:
- 23. Потенцирование логарифмических выраженийПереход от логарифмического выражения
- 24. Перейти к алгебраическому выражению
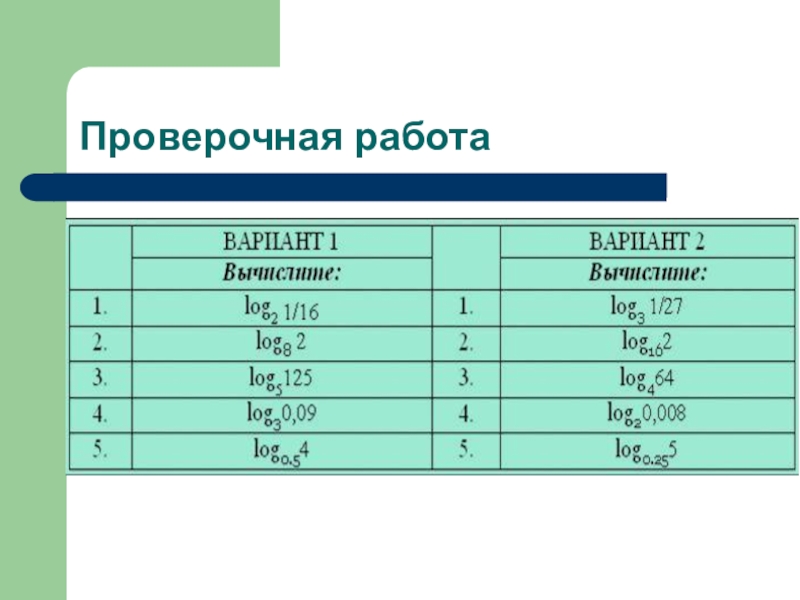
- 25. Проверочная работа
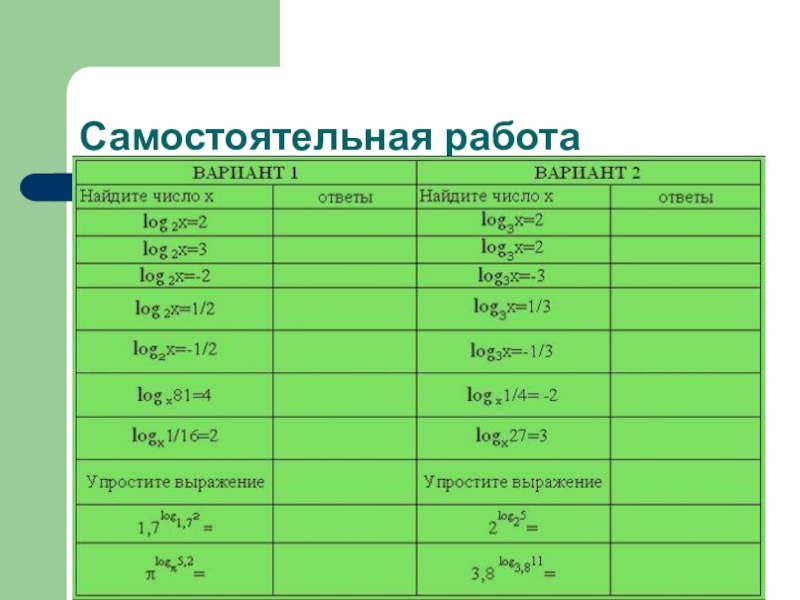
- 26. Самостоятельная работа
- 27. Работа в малых группах
- 28. Слайд 28
- 29. Домашнее задание1.п.14, 16 выучить свойства № 16.2;
ПОНЯТИЕ ЛОГАРИФМА« Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький» (Конфуций)
Слайд 1Муниципальное бюджетное общеобразовательное учреждение
лицей №35 г. Ставрополя
ПОНЯТИЕ ЛОГАРИФМА
Автор
Улитина Людмила Владимировна
Слайд 2ПОНЯТИЕ ЛОГАРИФМА
« Три пути ведут к знанию: путь размышления – это
путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький» (Конфуций)
Слайд 31. Сформировать: знание определения логарифм
- знание основного логарифмического тождества - знания основных свойств логарифмов: логарифм произведения; логарифм частного; логарифм степени
2.Формировать умения применять определение логарифма и основные свойства логарифмов при тождественных преобразований логарифмических выражений;
3.Способствовать развитию внимания, умению анализировать, сравнивать и делать выводы;
4.Продолжить формирование у учащихся навыков само и взаимоконтроля, вызывать у них потребность к обоснованию своих высказываний.
2.Формировать умения применять определение логарифма и основные свойства логарифмов при тождественных преобразований логарифмических выражений;
3.Способствовать развитию внимания, умению анализировать, сравнивать и делать выводы;
4.Продолжить формирование у учащихся навыков само и взаимоконтроля, вызывать у них потребность к обоснованию своих высказываний.
Цели:
Слайд 4Методы и организационные формы:
1.Индивидуальная работа;
2.Работа в парах;
3.Работа в малых группах.
Ресурсы:
1.Учебник «Алгебра и начала математического анализа»;
2.Компьютер и проектор.
Слайд 5Определение логарифма
Логарифмом числа в>0 по основанию а>0 и а
1 называется показатель степени, в которую нужно возвести число а, чтобы получить число в.
- логарифм с произвольным основанием.
- логарифм с произвольным основанием.
Слайд 7Свойства логарифмов
Логарифм произведения положительных чисел равен сумме логарифмов сомножителей:
Слайд 8Свойства логарифмов
Логарифм частного положительных чисел равен разности логарифмов делимого и делителя:
Слайд 9Свойства логарифмов
Логарифм степени положительного основания равен произведению показателя степени на логарифм
основания степени:
Слайд 21Логарифмирование
алгебраических выражений
Если число х представлено алгебраическим выражением, то логарифм любого
выражения можно выразить через логарифмы составляющих его чисел.
(на основании свойств логарифмов)
(на основании свойств логарифмов)
Слайд 23Потенцирование
логарифмических выражений
Переход от логарифмического выражения к алгебраическому называется потенцированием, то
есть, произвести действие, обратное логарифмированию
Слайд 29Домашнее задание
1.п.14, 16 выучить свойства № 16.2; 16.4; 16.7(в, г), 16.10(а,
г)
2. Доказать основные свойства логарифмов. (По желанию)
2. Доказать основные свойства логарифмов. (По желанию)