- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проектная работа учащихся 7 класса Хитрые задачи, которые нам по силам.
Содержание
- 1. Проектная работа учащихся 7 класса Хитрые задачи, которые нам по силам.
- 2. Проблема:С каждым годом наши одноклассники всё меньше
- 3. Цель проекта:Организовать помощь одноклассникам в обучении решению
- 4. Задачи проекта:1. Провести анкетирование одноклассников с целью
- 5. Вопросы анкеты:Согласны ли вы с тем, что:1)
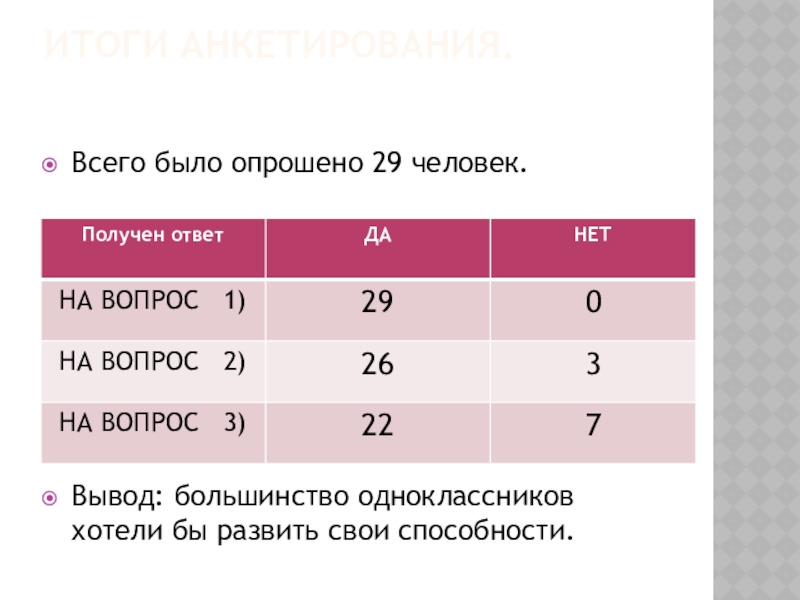
- 6. Итоги анкетирования.Всего было опрошено 29 человек.Вывод: большинство одноклассников хотели бы развить свои способности.
- 7. Задачи учебника и
- 8. № 151. На доске написаны числа 1,
- 9. № 354. Саша и Вася записывают 30-тизначное
- 10. № 432. В каждой клетке доски, размером
- 11. Попытайтесь решить наши задачи:№1. Аня и Маша
- 12. №2. В каждой клетке шахматной доски, размером
- 13. Желаем вам успехов в решении «хитрых» задач. Не бойтесь изобретать свои способы решения!
Слайд 1
Хитрые задачи, которые нам по силам.
Проектная работа по математике, выполненная учащимися
Сергеевым Глебом и
Серебряковой Анной
Слайд 2Проблема:
С каждым годом наши одноклассники всё меньше внимания обращают на задачи
Слайд 3Цель проекта:
Организовать помощь одноклассникам в обучении решению задач повышенной сложности.
Мотив выбора:
Мы
Слайд 4Задачи проекта:
1. Провести анкетирование одноклассников с целью изучения общественного мнения о
2. Решить четыре задачи, предлагаемых в учебнике «Алгебра 7» (авторы Мерзляк А.Г. и др.) в рубрике «Учимся делать нестандартные шаги».
3. Придумать (или подобрать из ранее известных) две своих задачи, в решении которых используются похожие принципы, и предложить одноклассникам их решить.
Слайд 5Вопросы анкеты:
Согласны ли вы с тем, что:
1) каждый человек уникален и
2) У каждого есть способности к какому-либо виду созидательной деятельности.
3) Эти способности каждый обязан развивать сам, используя для этого все возможности.
Слайд 6Итоги анкетирования.
Всего было опрошено 29 человек.
Вывод: большинство одноклассников хотели бы развить
Слайд 7Задачи учебника и
№ 32. Дано 12 натуральных чисел. Докажите, что из них всегда можно выбрать два, разность которых делится нацело на 11.
Решение: Заметим, что если каждое из чисел делить на 11, то получаются остатки от 0 до 10. Всего 11 остатков. Других остатков просто не бывает, т.к. остаток не должен быть больше делителя. А уж из двенадцати чисел всегда найдутся два, у которых одинаковый остаток от деления на 11. Разность таких чисел будет иметь остаток 0 при делении на 11. Значит, эта разность делится нацело на 11.
Слайд 8№ 151. На доске написаны числа 1, 2, 3, …,10. За
Решение: Заметим, что сумма всех чисел от 1 до 10 равна 45 – это нечётное число. После того, как мы к каждому из двух выбранных чисел добавим 5, сумма все чисел увеличится на 10, или на 20, или на 30 и т. д., но по прежнему останется нечётной. А если пару выбранных чисел уменьшать на 1, то сумма может меняться на 2, на 4, на 6, т.е. на чётное количество и, значит, сумма останется нечётной. Всего же чисел – 10 – чётное количество, а нечётные числа на чётные не делятся.
Ответ: Невозможно.
Слайд 9№ 354. Саша и Вася записывают 30-тизначное число, используя только цифры
Решение: Вспомним признак делимости на 9: сумма цифр числа должна делиться на 9 без остатка. Разобьём 30-тизначное число на 15 пар цифр. В каждой паре Саша пишет первую цифру, тогда Вася должен писать следующую цифру такую, чтобы она в сумме с предыдущей цифрой давала ровно 6. Заметим, что 15· 6 = 90 число, делящееся на 9. Почему мы разбили по парам? Так ведь играют два игрока.
Ответ: Не сможет.
Слайд 10№ 432. В каждой клетке доски, размером 5 на 5 сидит
Решение. Представим, что данная доска – шахматная, тогда она содержит 13 клеток одного цвета (например, белого) и 12 клеток другого цвета (например, чёрного). Все жуки при переползании должны попасть на поле другого цвета, но это невозможно, т.к. количества белых и чёрных полей не равны. Значит, обязательно останется пустая клетка одного цвета, и клетка с двумя жуками.
Ответ: Обязательно.
Слайд 11Попытайтесь решить наши задачи:
№1. Аня и Маша записывают 24-значное число, используя
т. д. Маша хочет получить число, кратное 9. Сможет ли Аня ей помешать?
Ответ: Не сможет.
Слайд 12№2. В каждой клетке шахматной доски, размером 7 на 7стоит пешка.
Ответ: Нет.