что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.
(В. Произволов)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок геометрии 11 класс Углы между плоскостями подготовка к ЕГЭ
Содержание
- 1. Урок геометрии 11 класс Углы между плоскостями подготовка к ЕГЭ
- 2. C2Углы между….Расстояния от…..прямыми; плоскостями. прямой и плоскостью;точки
- 3. « Углы между плоскостями»
- 4. Две пересекающиеся плоскости образуют …………………….
- 5. Составить уравнение плоскости
- 6. Слайд 6
- 7. Слайд 7
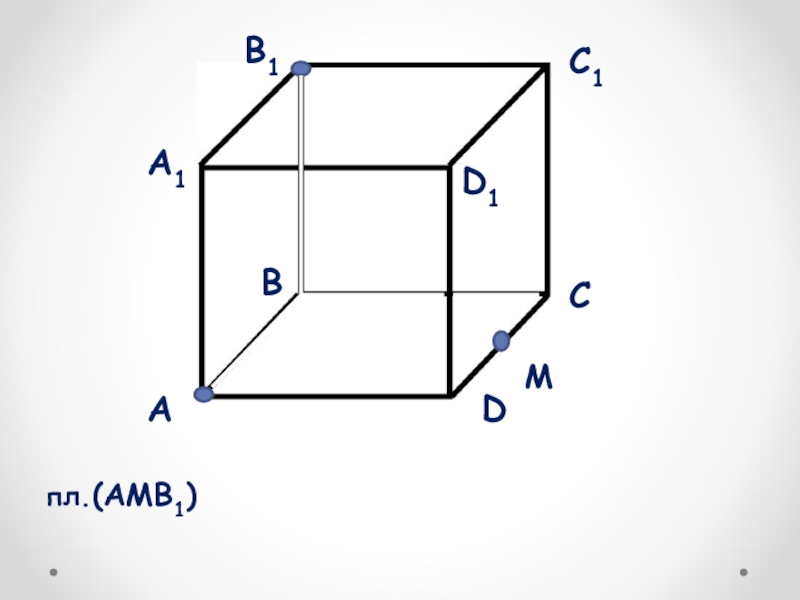
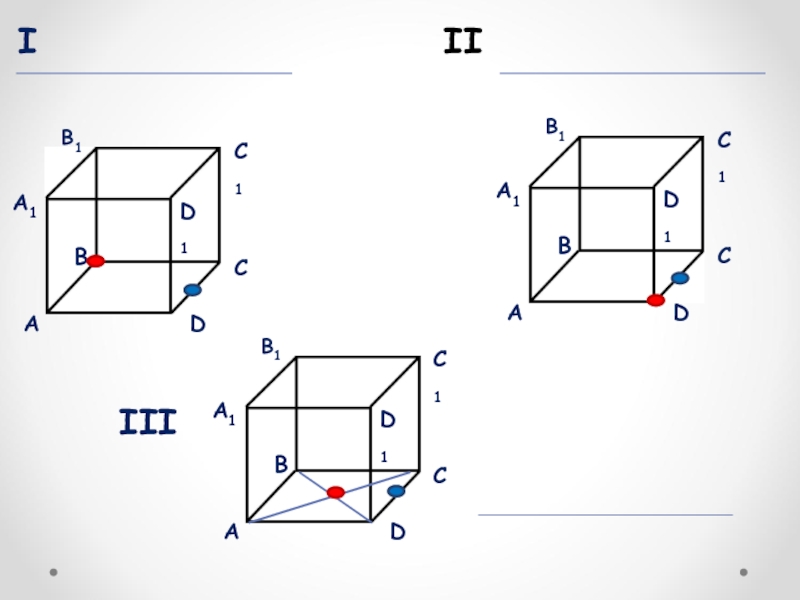
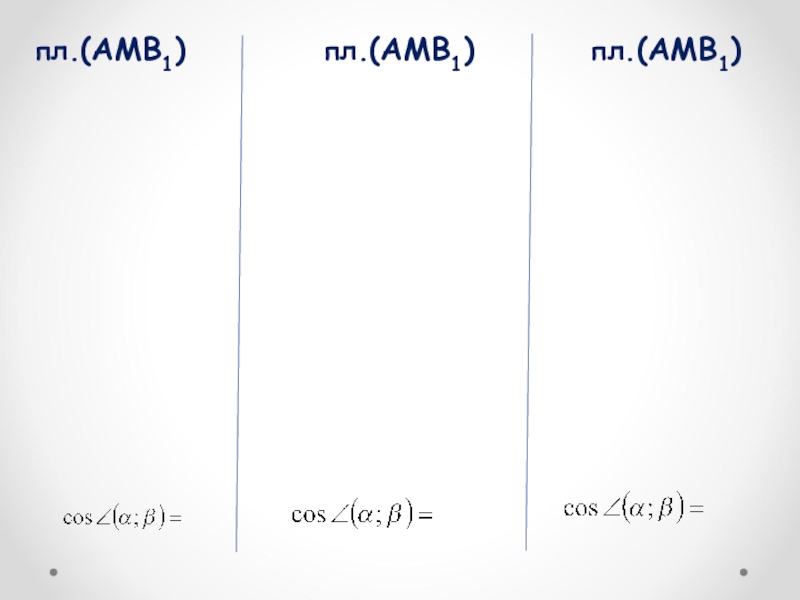
- 8. пл.(AMB1)пл.(AMB1)пл.(AMB1)
- 9. ипл.(АВС)
- 10. В правильной треугольной призме АВСА1В1С1 сторона основания
- 11. Слайд 11
- 12. Слайд 12
- 13. BHB1 = А…..F (по т. ……………………)
- 14. Решить задачу двумя способами
- 15. Рано или поздно всякая правильная математическая идея
- 16. Спасибо за урок!
- 17. http://www.csjonquiere.qc.ca/fichiers/images/big_devoirs___487____phototeque.jpg http://kostino.ucoz.ru/umor/13.jpg http://wiw21.volsk-sh-3.edusite.ru/images/0cb2c0928637.pnghttp://8.nezihsezer.com/ine_coordinate_geometry.pnghttp://novacia72.ru/d/383128/d/Nach-131.jpg
C2Углы между….Расстояния от…..прямыми; плоскостями. прямой и плоскостью;точки до прямой;скрещивающимися прямыми.точки до плоскости;
Слайд 2C2
Углы между….
Расстояния от…..
прямыми;
плоскостями.
прямой и плоскостью;
точки до прямой;
скрещивающимися
прямыми.
точки до плоскости;
Слайд 4Две пересекающиеся плоскости образуют ……………………. пары ………………. между собой
двугранных углов.
Величина двугранного угла измеряется величиной …………………………………… ……………………….. угла
Чтобы построить ………………………………. угол двугранного угла, надо взять на ………………………. ………………………………….. точку, и в каждой …………………….. провести к …………………… …………………………….. полупрямые.
Величина двугранного угла равна величине …………………… ……………….. этого двугранного угла.
Уравнение плоскости …………………………………………. .
Косинус угла между векторами равен …………………………………………
Косинус угла между плоскостями равен ……………………………………………….
Величина двугранного угла измеряется величиной …………………………………… ……………………….. угла
Чтобы построить ………………………………. угол двугранного угла, надо взять на ………………………. ………………………………….. точку, и в каждой …………………….. провести к …………………… …………………………….. полупрямые.
Величина двугранного угла равна величине …………………… ……………….. этого двугранного угла.
Уравнение плоскости …………………………………………. .
Косинус угла между векторами равен …………………………………………
Косинус угла между плоскостями равен ……………………………………………….
Слайд 10В правильной треугольной призме АВСА1В1С1
сторона основания равна 1, а боковое
ребро равно 2, точка
D – середина СС1. Найдите угол между пл. (АВС) и пл.(ADB1).
D – середина СС1. Найдите угол между пл. (АВС) и пл.(ADB1).
Слайд 11
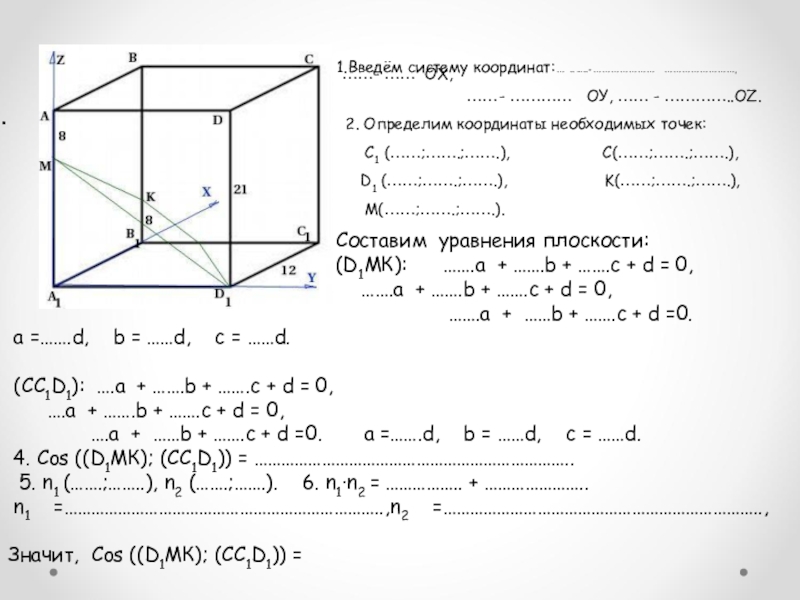
1.Введём систему координат:… .. …..- ………………… ……………………,
……- ………… ОУ, …… - …………..ОZ.
2. Определим координаты необходимых точек:
С1 (……;…….;…….), С(……;…….;…….),
D1 (……;…….;…….), K(……;…….;…….),
М(……;…….;…….).
Составим уравнения плоскости:
(D1МК): …….a + …….b + …….c + d = 0,
…….a + …….b + …….c + d = 0,
…….a + ……b + …….c + d =0.
a =…….d, b = ……d, c = ……d.
(CC1D1): ….a + …….b + …….c + d = 0,
….a + …….b + …….c + d = 0,
….a + ……b + …….c + d =0. a =…….d, b = ……d, c = ……d.
4. Cos ((D1МК); (CC1D1)) = ……………………………………………………………..
5. n1 (…….;……..), n2 (…….;…….). 6. n1·n2 = …………….. + …………………..
n1 =……………………………………………………………..,n2 =……………………………………………………………..,
Значит, Cos ((D1МК); (CC1D1)) =
……- ………… ОУ, …… - …………..ОZ.
2. Определим координаты необходимых точек:
С1 (……;…….;…….), С(……;…….;…….),
D1 (……;…….;…….), K(……;…….;…….),
М(……;…….;…….).
Составим уравнения плоскости:
(D1МК): …….a + …….b + …….c + d = 0,
…….a + …….b + …….c + d = 0,
…….a + ……b + …….c + d =0.
a =…….d, b = ……d, c = ……d.
(CC1D1): ….a + …….b + …….c + d = 0,
….a + …….b + …….c + d = 0,
….a + ……b + …….c + d =0. a =…….d, b = ……d, c = ……d.
4. Cos ((D1МК); (CC1D1)) = ……………………………………………………………..
5. n1 (…….;……..), n2 (…….;…….). 6. n1·n2 = …………….. + …………………..
n1 =……………………………………………………………..,n2 =……………………………………………………………..,
Значит, Cos ((D1МК); (CC1D1)) =
……- …… ОХ,
Слайд 13BHB1 =
А…..F (по т. ……………………) AF2 =……………………………………………………
и (………….).
Для этого построим сечение ………………………
плоскостью (…………..)
плоскостью (…………..)
Слайд 15Рано или поздно всякая правильная математическая идея находит применение в том
или ином деле. (А.Н. Крылов)