А Ч
П О Т Е О Р И И
В Е Р О Я Т Н О С Т Е Й
(задание №5 ЕГЭ)
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок алгебры в 10 классе Решение задач теории вероятностей
Содержание
- 1. Урок алгебры в 10 классе Решение задач теории вероятностей
- 2. Основные понятия теории вероятностейСлучайным называется событие, которое
- 3. Вероятность события А если n -
- 4. №1. Игральный кубик бросают один раз,
- 5. Пример №2.В соревнованиях по толканию ядра участвуют
- 6. Пример №3. Бросили две игральные кости. Найти
- 7. Вероятность события Р(А) события А и вероятность
- 8. Пример №4. Вероятность того, что шариковая ручка
- 9. Пример №5. В некотором городе из 5000
- 10. Сложение вероятностей Суммой несовместных событий A и
- 11. Пример №6. В ящике
- 12. Произведение вероятностей Произведением событий A
- 13. Пример №7. Дважды бросается игральный кубик. Какова
- 14. Пример №8. В торговом центре два
- 15. Вероятность суммы двух независимых событий равна
- 16. Пример №9. В магазине два платежных автомата.
- 17. Выполните задания самостоятельно!!!
Основные понятия теории вероятностейСлучайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.Испытанием называют такое действие, которое может привести к одному из нескольких результатов.
Слайд 2Основные понятия теории вероятностей
Случайным называется событие, которое нельзя точно предсказать заранее.
Оно может либо произойти, либо нет.
Испытанием называют такое действие, которое может привести к одному из нескольких результатов.
Испытанием называют такое действие, которое может привести к одному из нескольких результатов.
Слайд 3Вероятность события А
если n - число всех исходов
некоторого испытания,
а m - число благоприятствующих событию A исходов,
то вероятность события A равна
P(A) =
а m - число благоприятствующих событию A исходов,
то вероятность события A равна
P(A) =
Слайд 4№1.
Игральный кубик бросают один раз, какова вероятность того, что
выпадет число 4.
Решение
У кубика 6 сторон, выпасть может любая из них, значит число всех исходов равно n = 6. Число 4 может выпасть только в одном случае, т.е. число благоприятствующих исходов равно m = 1.
Тогда при n = 6, m = 1,
вероятность равна P(A) = .
Ответ:
Решение
У кубика 6 сторон, выпасть может любая из них, значит число всех исходов равно n = 6. Число 4 может выпасть только в одном случае, т.е. число благоприятствующих исходов равно m = 1.
Тогда при n = 6, m = 1,
вероятность равна P(A) = .
Ответ:
Слайд 5Пример №2.
В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии,
7 - из Дании, 9 - из Швеции и 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение:
всего спортсменов 4+7+9+5 = 25 значит n = 25,
вероятность события A – «последний спортсмен из Швеции», а их всего 9, т.е. m = 9
Решение:
всего спортсменов 4+7+9+5 = 25 значит n = 25,
вероятность события A – «последний спортсмен из Швеции», а их всего 9, т.е. m = 9
Ответ: 0,36.
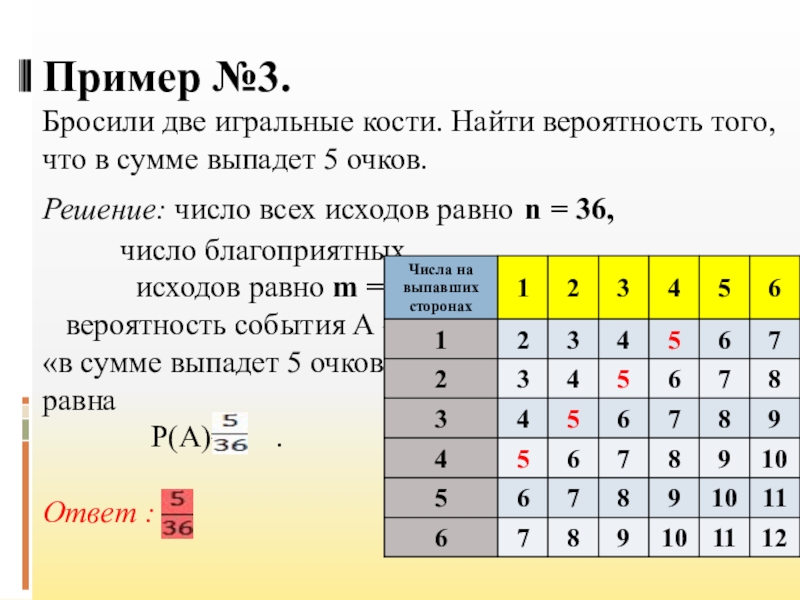
Слайд 6Пример №3. Бросили две игральные кости. Найти вероятность того, что в сумме
выпадет 5 очков.
Решение: число всех исходов равно n = 36,
число благоприятных
исходов равно m = 4,
вероятность события А –
«в сумме выпадет 5 очков»
равна
Р(А)= .
Ответ :
Слайд 7Вероятность события Р(А) события А и вероятность Р( )
противоположного ему события связаны соотношением:
Р(А) + Р( ) = 1
Слайд 8Пример №4. Вероятность того, что шариковая ручка пишет плохо (или не пишет)
равна 0,1. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что ручка пишет хорошо.
Решение:
событие А – «ручка пишет хорошо»,
событие противоположное ему Р( ) = 0,1
Р(А) + Р( ) = 1
Р(А) = 1 – Р( )
Р(А) = 1 – 0,1 = 0,9.
Ответ: 0,9.
Слайд 9Пример №5. В некотором городе из 5000 появившихся на свет младенцев оказалось
2512 мальчиков. Найдите, чему равна вероятность рождения девочек. Результат округлите до тысячных.
Решение:
5000 – 2512 = 2488 (ч.) – девочки.
Вероятность появления на свет девочки равна
Ответ: 0,498.
Слайд 10Сложение вероятностей
Суммой несовместных событий A и B называют событие A
+ B, состоящее в появлении
либо только события A,
либо только события B:
P(A+B) = P(A) + P(B)
либо только события A,
либо только события B:
P(A+B) = P(A) + P(B)
Слайд 11Пример №6. В ящике лежат 10 шаров: 4 красных,
1 синий и 5 черных. Наугад вынимается один шар. Какова вероятность того, что шар красный или синий.
Решение :
событие A – «вынут красный шар» P(A) = = 0,4
событие B – «вынут синий шар» P(B) = = 0,1
Тогда вероятность того, что
«вынутый шар красный или синий» равна
P(A+B) = 0,4 + 0,1 = 0,5.
Ответ: 0,5.
Слайд 12Произведение вероятностей Произведением событий A и B называется событие A B,
состоящее в появлении
и события A и события B
P(AB) = P(A) P(B)
Слайд 13Пример №7. Дважды бросается игральный кубик. Какова вероятность того что оба раза
выпадет число 5.
Решение:
пусть событие A – «1-й раз выпадет 5» и событие B – «2-й раз выпадет 5». Вероятности этих событий
P(A) = P(B) =
Тогда вероятность Р(АВ) того, что «оба раза выпадет число 5» :
P(AB) = .
Ответ: .
Слайд 14 Пример №8. В торговом центре два одинаковых автомата продают кофе. Каждый
из них может быть не исправен с вероятностью 0,12 независимо друг от друга. Найти вероятность того, что хотя бы один автомат исправен.
Решение:
событие А – «1-й автомат не исправен» и событие В – «2-й автомат на исправен» имеют вероятности
Р(А) = Р(В) = 0,12. Тогда Р(АВ) – «оба автомата не исправны» Р(АВ) = Р(А) Р(В) = 0,12 0,12 = 0,0144.
Вероятность события - «хотя бы один автомат исправен», т.е. Р( ) = 1 – 0,0144 = 0,9856.
Ответ: 0,9856.
Слайд 15Вероятность суммы двух независимых событий равна разности суммы вероятностей этих событий
и произведения вероятностей этих событий:
Р(А+В) = Р(А) + Р(В) – Р(А)Р(В)
Слайд 16Пример №9. В магазине два платежных автомата. Вероятность того, что в автомате
к концу дня закончатся деньги, равна 0,02 независимо от другого автомата. Вероятность того, что деньги закончатся в обеих автоматах, равна 0,015. Найти вероятность того, что к концу дня деньги останутся в обеих автоматах.
Решение: А – «деньги закончились в 1- м автомате», В – «деньги закончились во 2- м автомате» Р (А) = Р(В) = 0,02.
«Деньги закончились в обеих автоматах» Р(А∙В) = 0,015. «Деньги закончатся хотя бы в одном автомате»:
Р(А+В) = Р(А) + Р(В) - Р(А∙В)
Р(А+В) = 0,02 + 0,02 – 0,015 = 0,025.
Вероятность «Деньги останутся в обеих автоматах» равна
Р( ) = 1 – 0,025 = 0,975.
Ответ: 0,975.