СОШ №1 п.г.т Ноглики
Агиенко Татьяна Ивановна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Уравнение с двумя переменными и его график 9 кл.ppt
Содержание
- 1. Уравнение с двумя переменными и его график 9 кл.ppt
- 2. Каждое из уравненийявляется уравнением с двумя переменными.
- 3. ;;Общие виды уравнений с двумя переменными:
- 4. Определите, является ли решениемуравнения х – у2
- 5. Уравнение с двумя переменными
- 6. Слайд 6
- 7. Определите степень уравненияу + х2 = 0х2
- 8. Графиком уравнения с
- 9. ГРАФИКИ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ ДЕКАРТОВ ЛИСТх2
- 10. КЛОФОИДА«Клофо» – от греч. «прясть». Клофоида
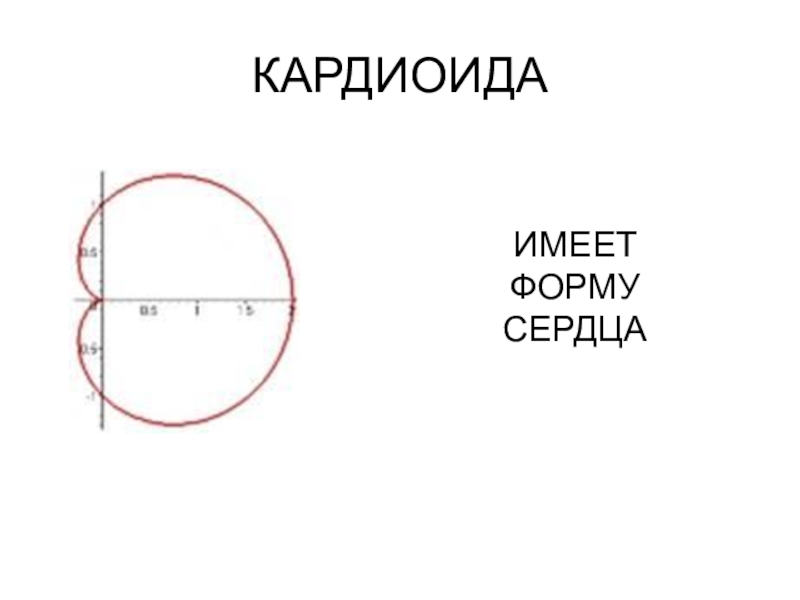
- 11. КАРДИОИДАИМЕЕТ ФОРМУ СЕРДЦА
- 12. Слайд 12
- 13. ;;;
- 14. у + х2 = 0х2 + (у
- 15. 3 х + 2 у = 5
- 16. №395(а;б); №396(г;в); №397(а;в); №399(а;б;д;ж);Самостоятельная работа:№395(в); №396(б); №399(е); №399(е;з); Домашнее задание:Пункт 17.№395(г); №396(а); №397(г); №399(в;г;е;з);) Урок №1
- 17. №400; №402(в;г); №404(а); №405(б); №410(а)Самостоятельная работа:№401(б;г);№404(б); Дополнительно:
Каждое из уравненийявляется уравнением с двумя переменными.
Слайд 4Определите, является ли решением
уравнения
х – у2 – 1 =
0 пара чисел?
а) (0; -1); в) (1;1);
б) (2; -1); г) (5; - 2).
а) (0; -1); в) (1;1);
б) (2; -1); г) (5; - 2).
Решением уравнения с двумя переменными называется пара значений переменных,
обращающая это уравнение в верное равенство.
Слайд 5 Уравнение с двумя переменными
имеет, как правило, бесконечное
множество решений
Два уравнения, имеющие одно и тоже
множество решений, называют
равносильными уравнениями.
Слайд 7Определите степень уравнения
у + х2 = 0
х2 + (у + 2)2
= 9
3 х + 2 у = 5
х у = 8
(х – 3)2 + (у + 2)2 = 0
3 х + 2 у = 5
х у = 8
(х – 3)2 + (у + 2)2 = 0
Слайд 8 Графиком уравнения с двумя
переменными называется
множество точек
координатной
плоскости, координаты которых
обращают уравнение в верное
равенство.
плоскости, координаты которых
обращают уравнение в верное
равенство.
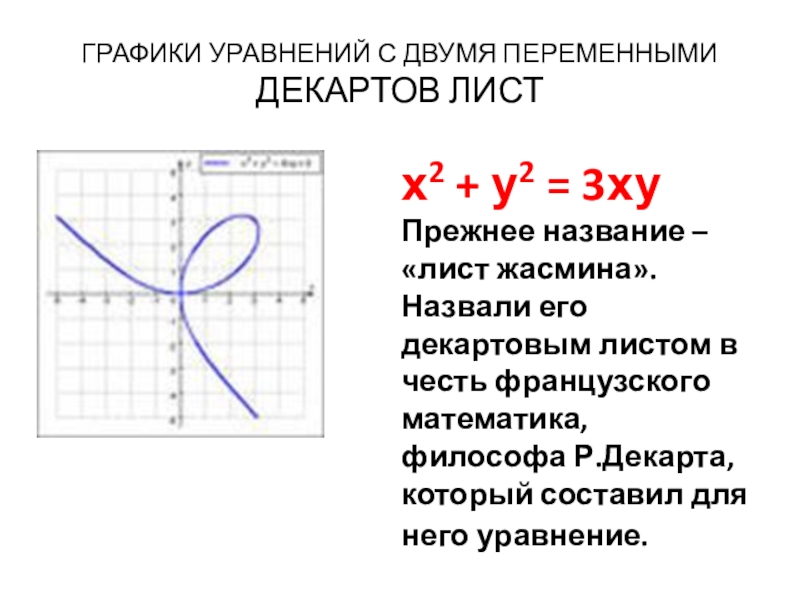
Слайд 9ГРАФИКИ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
ДЕКАРТОВ ЛИСТ
х2 + у2 = 3ху
Прежнее название
– «лист жасмина». Назвали его декартовым листом в честь французского математика, философа Р.Декарта, который составил для него уравнение.
Слайд 10
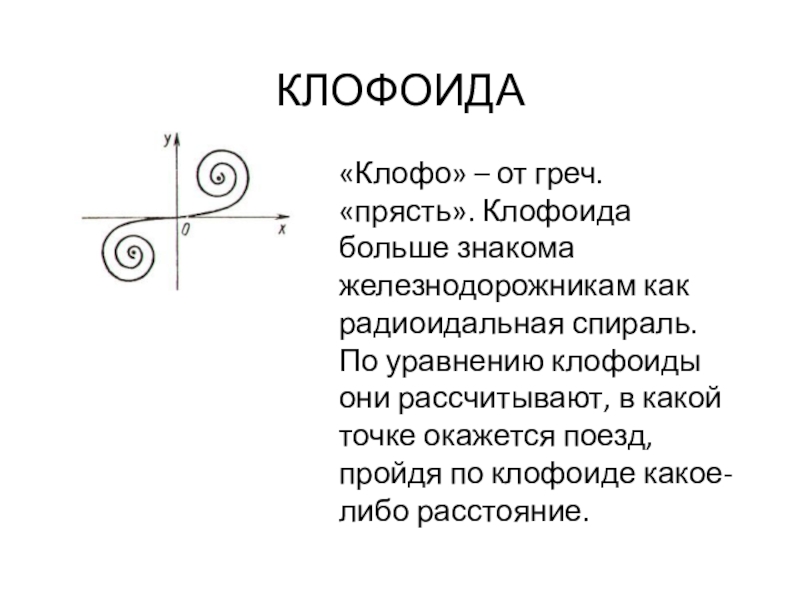
КЛОФОИДА
«Клофо» – от греч. «прясть». Клофоида больше знакома железнодорожникам как радиоидальная
спираль. По уравнению клофоиды они рассчитывают, в какой точке окажется поезд, пройдя по клофоиде какое-либо расстояние.
Слайд 14у + х2 = 0
х2 + (у + 2)2 = 9
Какой
фигурой является график каждого из уравнений?
Парабола
(Х-0)2 + (у + 2)2 = 9
Окружность с центром в точке (0; - 2)
и R = 3.
х2 + у 2 = 25
Окружность с центром в точке (0;0)
и R = 5.
Слайд 153 х + 2 у = 5
х у = 8
(х – 3)2 + (у + 2)2 = 0
Гипербола.
Окружность с центром в точке (3; - 2).
Прямая.
Какой фигурой является график каждого из уравнений?
Слайд 16№395(а;б); №396(г;в); №397(а;в); №399(а;б;д;ж);
Самостоятельная работа:
№395(в); №396(б); №399(е); №399(е;з);
Домашнее задание:
Пункт 17.
№395(г);
№396(а); №397(г); №399(в;г;е;з);)
Урок №1
Слайд 17№400; №402(в;г); №404(а); №405(б); №410(а)
Самостоятельная работа:
№401(б;г);
№404(б);
Дополнительно: №407
Домашнее задание:
Пункт 17.
№401(а;в);
№402(а); №403; №404(в); №405(в); №410(б); №420(б); № 422(б)
Урок №2
