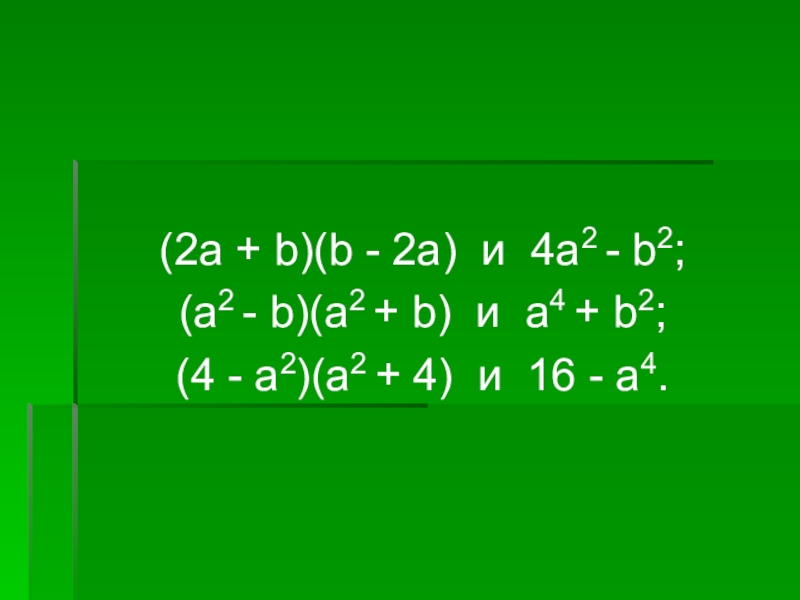- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Умножение разности двух выражений на их сумму
Содержание
- 1. Умножение разности двух выражений на их сумму
- 2. Устно1. Прочитай выражение: а) m-n; m+n; -m+n;
- 3. Проверь себя.Вариант 1.№1 в)№2 в)№3 а) −
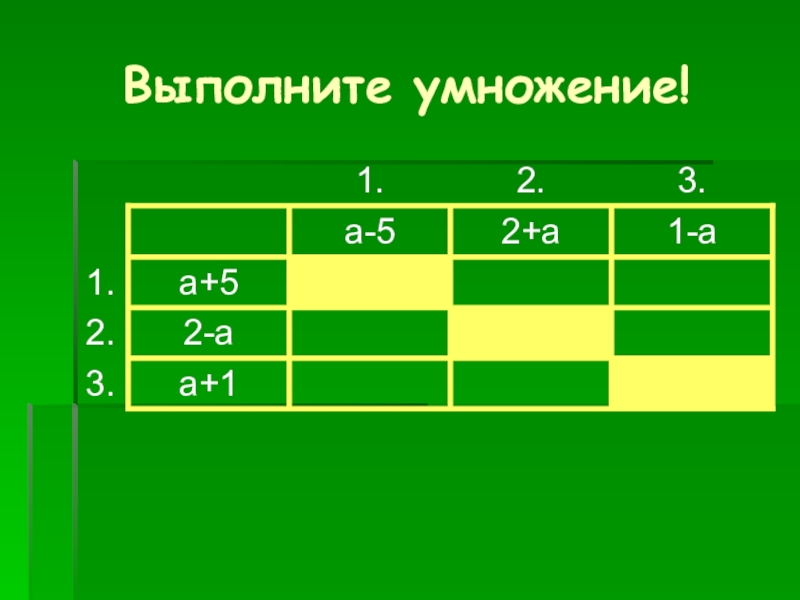
- 4. Выполните умножение!
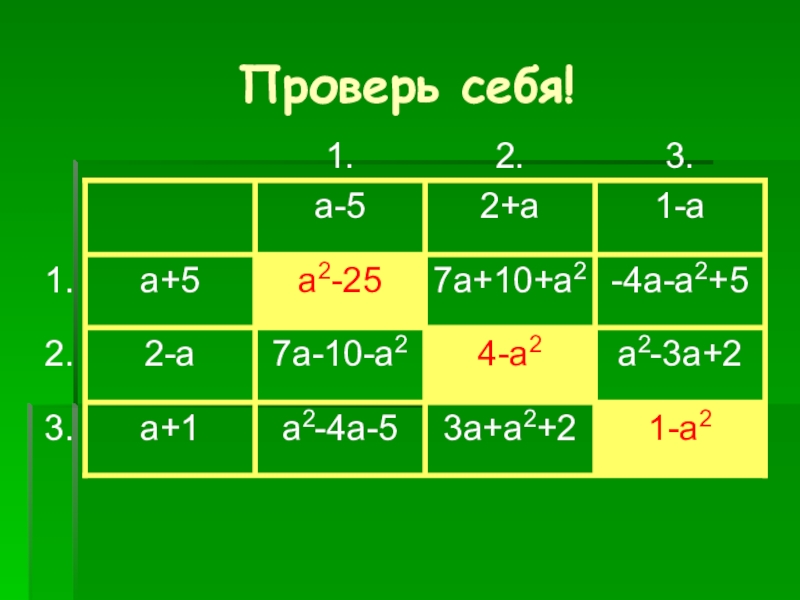
- 5. Проверь себя!
- 6. (2а + b)(b - 2a) и 4a2
- 7. Преобразуйте произведения в многочлен.
- 8. Проверь себя!С Е М И О Т И К А
- 9. Применение.(100 + 1)(100 - 1) = 1002
- 10. Спасибо за урок!
Устно1. Прочитай выражение: а) m-n; m+n; -m+n; 2m-3n. б) m2-n2; m2+n2; (3a)2-(2b)2; a2-25. в) (b-c)2; (a+2c)2; (-x-y)2.2. Возведи в квадрат: 8с; 0,9a; 1/4 x; 2/7 a3; 0,05y2.
Слайд 2Устно
1. Прочитай выражение:
а) m-n; m+n; -m+n; 2m-3n.
б) m2-n2; m2+n2; (3a)2-(2b)2;
a2-25.
в) (b-c)2; (a+2c)2; (-x-y)2.
2. Возведи в квадрат:
8с; 0,9a; 1/4 x; 2/7 a3; 0,05y2.
в) (b-c)2; (a+2c)2; (-x-y)2.
2. Возведи в квадрат:
8с; 0,9a; 1/4 x; 2/7 a3; 0,05y2.
Слайд 3
Проверь себя.
Вариант 1.
№1 в)
№2 в)
№3 а) − 2; б) − 3;
в) − 1
№4 б)
№5 3а2+3
№4 б)
№5 3а2+3
Вариант 2.
№1 б)
№2 б)
№3 а) − 3; б) − 1; в) − 2
№4 а)
№5 4+4х2
Оцени себя: на «5» - 4
на «4» - 3
на «3» - 2
Вариант 1.
№1 в)
№2 в)
№3 а) − 2; б) − 3; в) − 1
№4 б)
№5 3а2+3
Вариант 1.
№1 в)
№2 в)
№3 а) − 2; б) − 3; в) − 1
№4 б)
№5 3а2+3
Слайд 9Применение.
(100 + 1)(100 - 1) = 1002 - 12 =
= 10
000 - 1 = 9 999
37∙43 = (40 - 3)(40 + 3) = 402 -32=
= 1 600 - 9 = 1 591
37∙43 = (40 - 3)(40 + 3) = 402 -32=
= 1 600 - 9 = 1 591