- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема Виета (8 класс)
Содержание
- 1. Теорема Виета (8 класс)
- 2. Определение приведенного квадратного уравнения Квадратное уравнение называется приведенным, если его старший коэффициент равен 1.
- 3. Выбери приведенные квадратные уравненияХ2-5х+6=02х2+3х+1=0Х2-2х-15=03х2-7х+3=0Х2+6х+8=0Х2-3х-18=0Х2+4х-5=0Х2-5х+6=0Х2-2х-15=0Х2+6х+8=0Х2-3х-18=0Х2+4х-5=0
- 4. Слайд 4
- 5. тема урока: Теорема Виета
- 6. Слайд 6
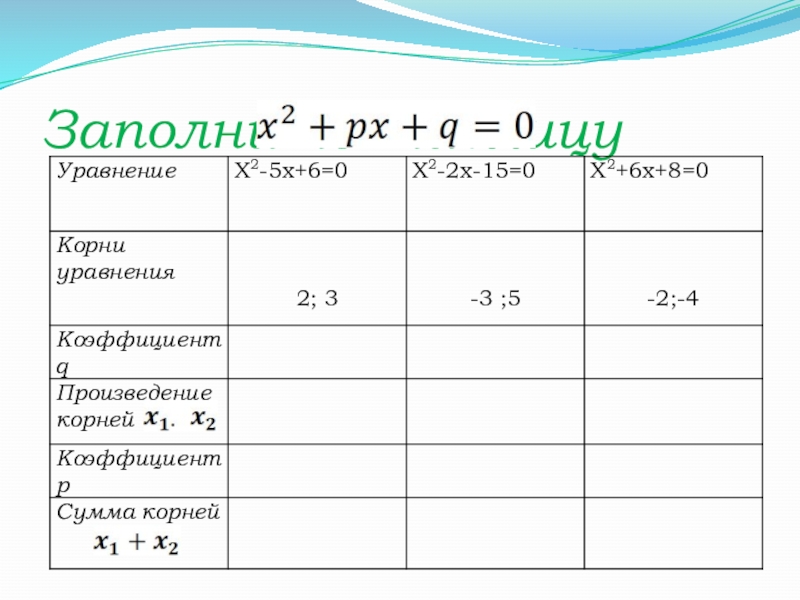
- 7. Заполните таблицу
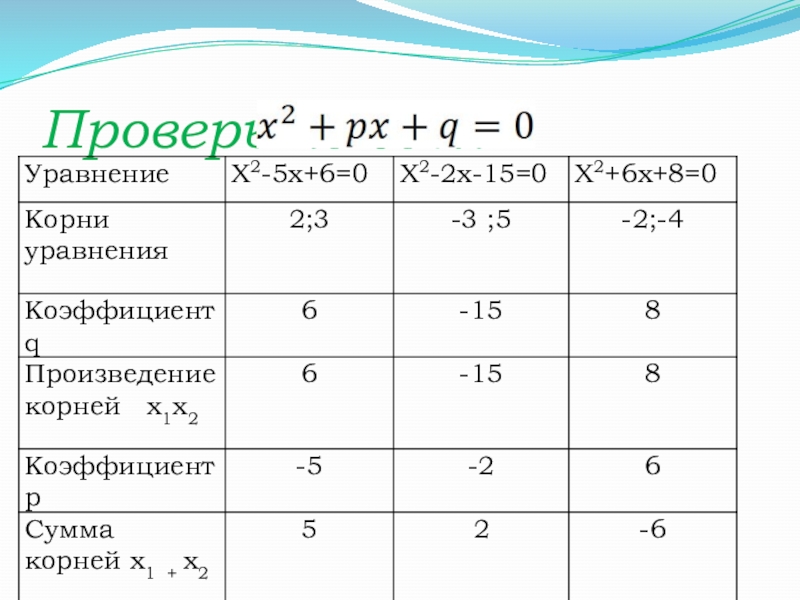
- 8. Проверьте себя
- 9. Заполните пропускиСумма корней --------------квадратного уравнения
- 10. Заполните пропуски ----------корней приведенного квадратного уравнения
- 11. Найдите уравнение ,корнями которого являются числа 3 и -5 Х2 -2х-15=0Х2 +8х+15=0Х2 -15х-8=0Х2+2х-15=0Х2+2х-15=0
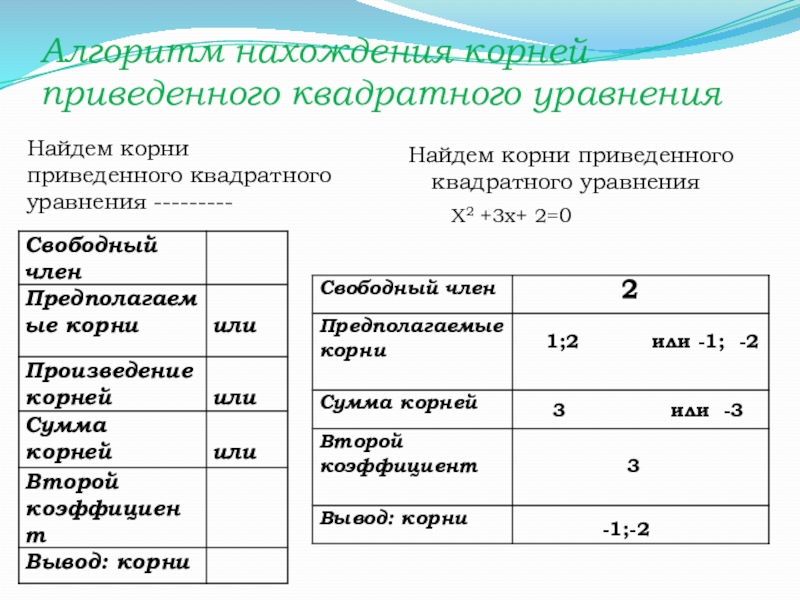
- 12. Алгоритм нахождения корней приведенного квадратного уравнения
- 13. Запишите на математическом языке теорему Виета для приведенного квадратного уравнения
- 14. Проверка самостоятельной работы1 вариант № 29.6 (б)
- 15. Информация о домашнем задании№ 29.8 (в,г) ,п.29,сообщение из Интернета о Франсуа Виете.
- 16. Слайд 16
- 17. С какой проблемой вы столкнулись в начале
- 18. Слайд 18
Определение приведенного квадратного уравнения Квадратное уравнение называется приведенным, если его старший коэффициент равен 1.
Слайд 2Определение приведенного квадратного уравнения
Квадратное уравнение называется приведенным, если его
старший коэффициент равен 1.
Слайд 3Выбери приведенные квадратные уравнения
Х2-5х+6=0
2х2+3х+1=0
Х2-2х-15=0
3х2-7х+3=0
Х2+6х+8=0
Х2-3х-18=0
Х2+4х-5=0
Х2-5х+6=0
Х2-2х-15=0
Х2+6х+8=0
Х2-3х-18=0
Х2+4х-5=0
Слайд 4
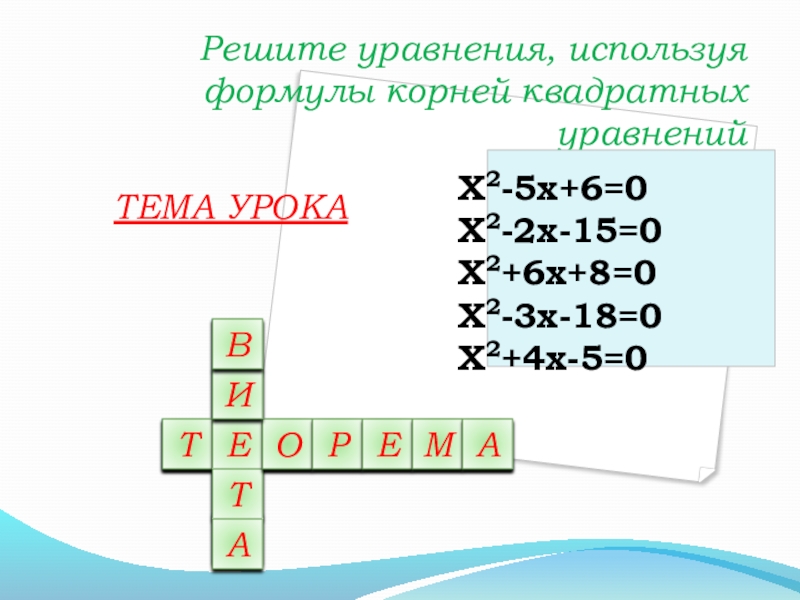
Решите уравнения, используя формулы корней квадратных уравнений
Х2-5х+6=0
Х2-2х-15=0
Х2+6х+8=0
Х2-3х-18=0
Х2+4х-5=0
2
-4
2
1
-5
-4
3
-3
5
-2
-3
Т
Е
Т
А
О
Р
Е
М
А
И
В
ТЕМА УРОКА
Слайд 9Заполните пропуски
Сумма корней --------------
квадратного уравнения равна второму коэффициенту,
-------------------------------------------------------,
а
–------------------------
корней равно свободному члену.
корней равно свободному члену.
приведенного
взятому с противоположным знаком
произведение
Слайд 10Заполните пропуски
----------корней приведенного квадратного уравнения
равна --------------
коэффициенту, взятому с противоположным знаком, а произведение корней равно---------------------------.
Сумма
второму
свободному члену
Слайд 11
Найдите уравнение ,корнями которого являются числа
3 и -5
Х2 -2х-15=0
Х2 +8х+15=0
Х2
-15х-8=0
Х2+2х-15=0
Х2+2х-15=0
Х2+2х-15=0
Слайд 12
Алгоритм нахождения корней приведенного квадратного уравнения
Найдем корни приведенного квадратного уравнения
Найдем
корни приведенного квадратного уравнения ---------
2
1;2
3
или -3
3
-1;-2
-2
или -1;
Х2 +3х+ 2=0
Слайд 14Проверка самостоятельной работы
1 вариант
№ 29.6 (б)
14; 1
29.9 (г)
х2+8х+12=0
2 вариант
№ 29.6 (в)
-1;-7
29.9 (в)
х2+7х-8=0
Слайд 17
С какой проблемой вы столкнулись в начале урока?
С помощью чего удалось
решить проблему?
Чему необходимо научиться еще, чтобы быстро решать приведенные квадратные уравнения?
Можно ли не приведенное квадратное уравнение решить по теореме Виета?
Чему необходимо научиться еще, чтобы быстро решать приведенные квадратные уравнения?
Можно ли не приведенное квадратное уравнение решить по теореме Виета?