- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема синусов, теорема косинусов
Содержание
- 1. Теорема синусов, теорема косинусов
- 2. Цели урока: 1) выработать умения и навыки
- 3. План урока: ПовторениеУстные упражненияТеорема синусовТеорема косинусовПрактические упражненияПодберите чертежПодберите условиеРешите задачи ВопросыДомашнее заданиеРефлексия12
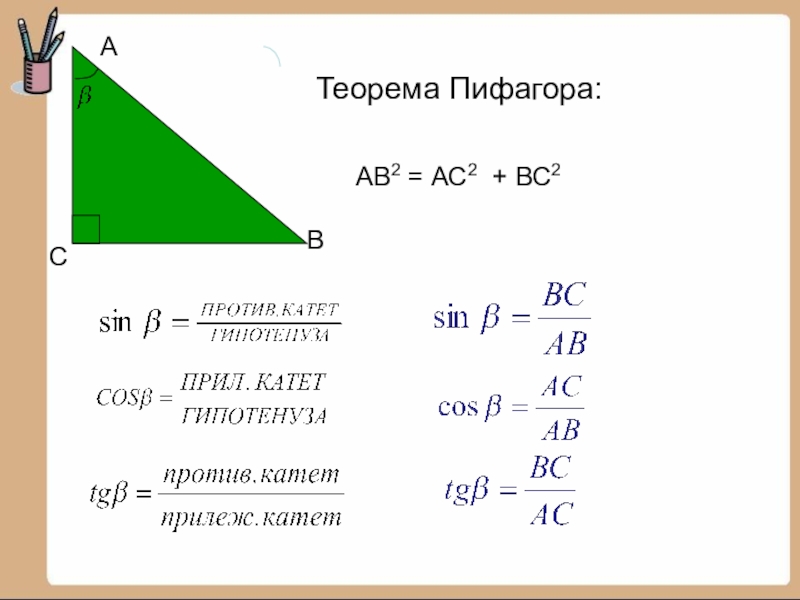
- 4. САВАВ2 = АС2 + ВС2Теорема Пифагора:
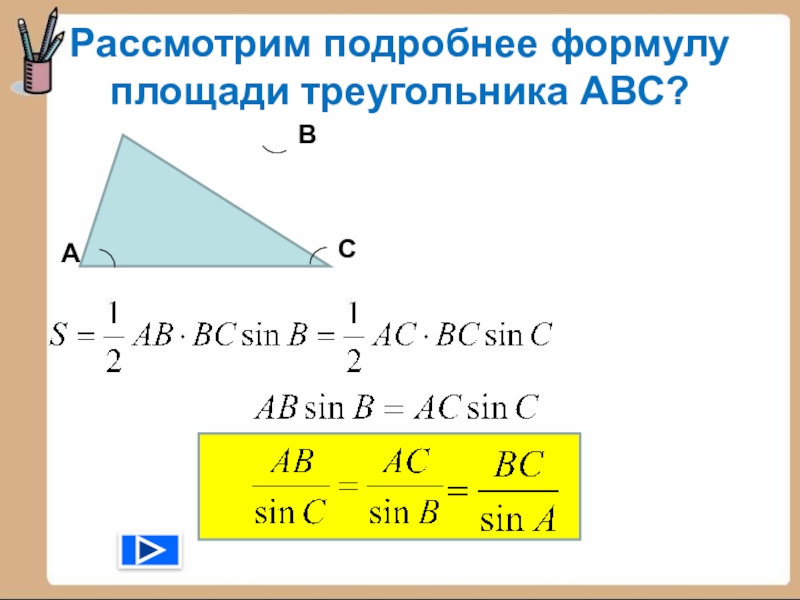
- 5. Сформулируйте теорему о площади треугольника?Площадь треугольника равна
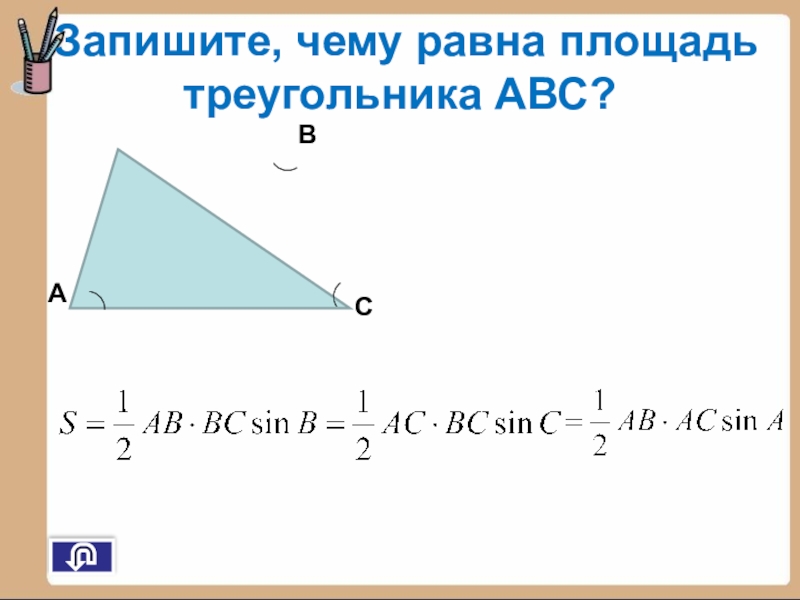
- 6. Запишите, чему равна площадь треугольника АВС? АВС
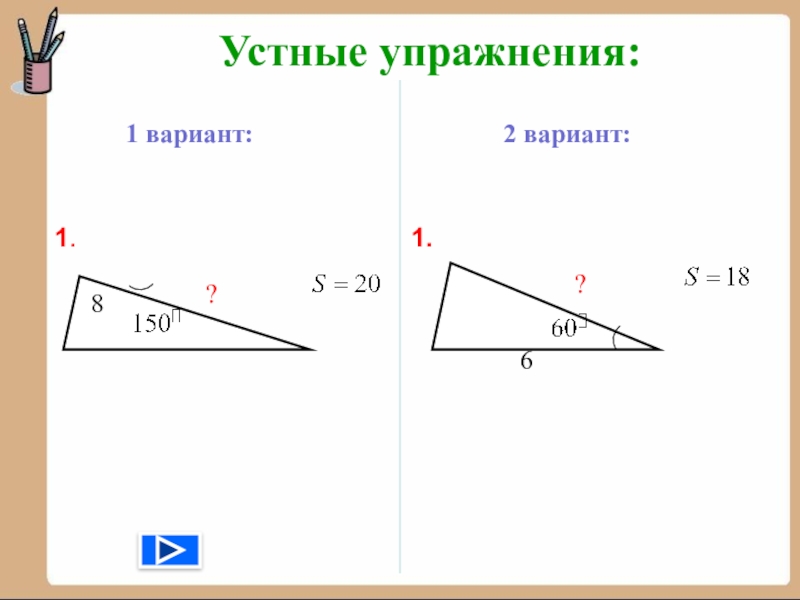
- 7. Устные упражнения:1 вариант:2 вариант:8??61.1.
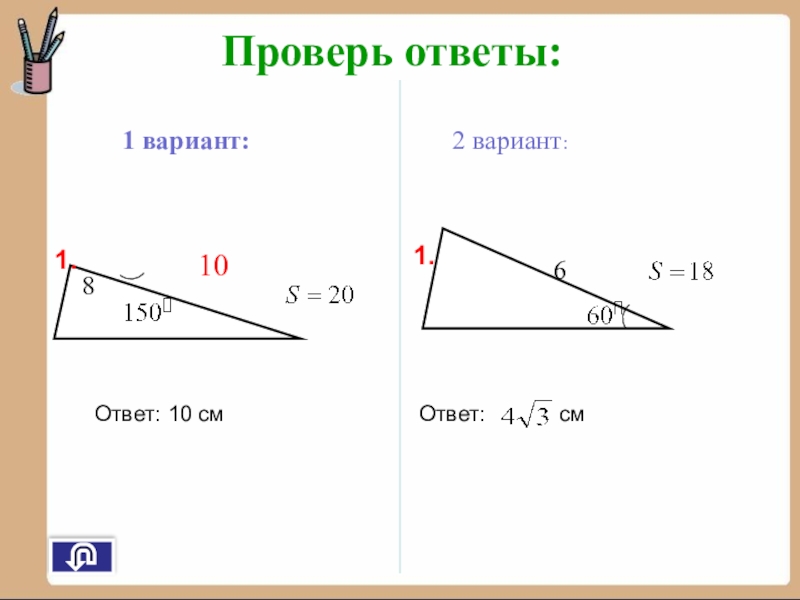
- 8. Проверь ответы:1 вариант:2 вариант:8106Ответ: 10 смОтвет: см1.1.2 вариант:
- 9. Рассмотрим подробнее формулу площади треугольника АВС? АВС
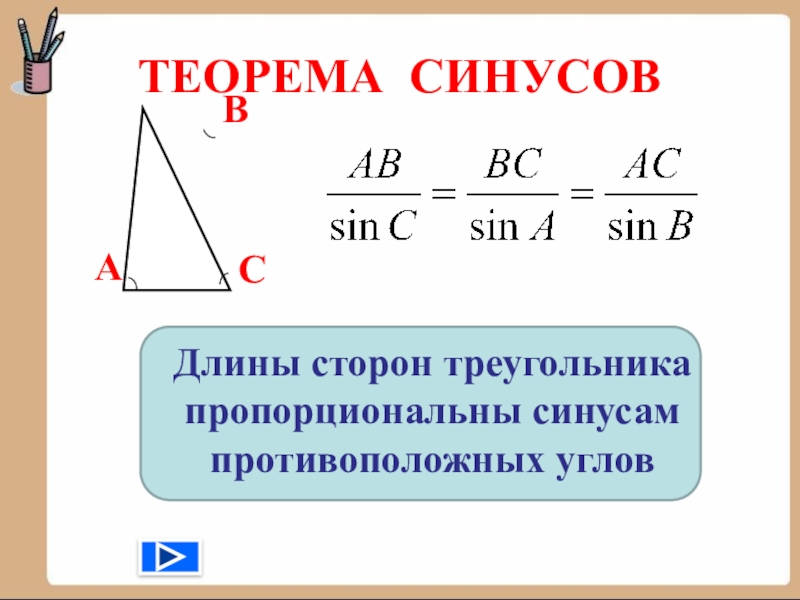
- 10. ТЕОРЕМА СИНУСОВДлины сторон треугольника пропорциональны синусам противоположных угловАВС
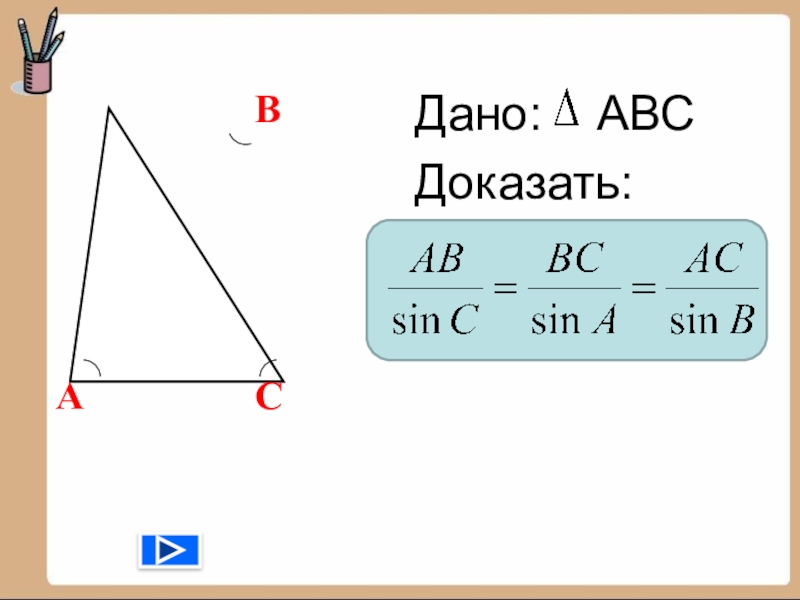
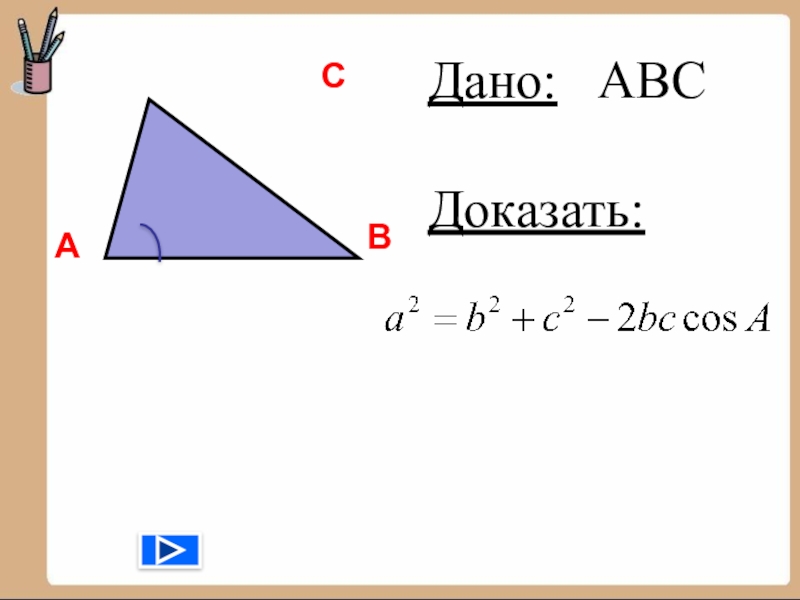
- 11. Дано: АВСДоказать: АВС
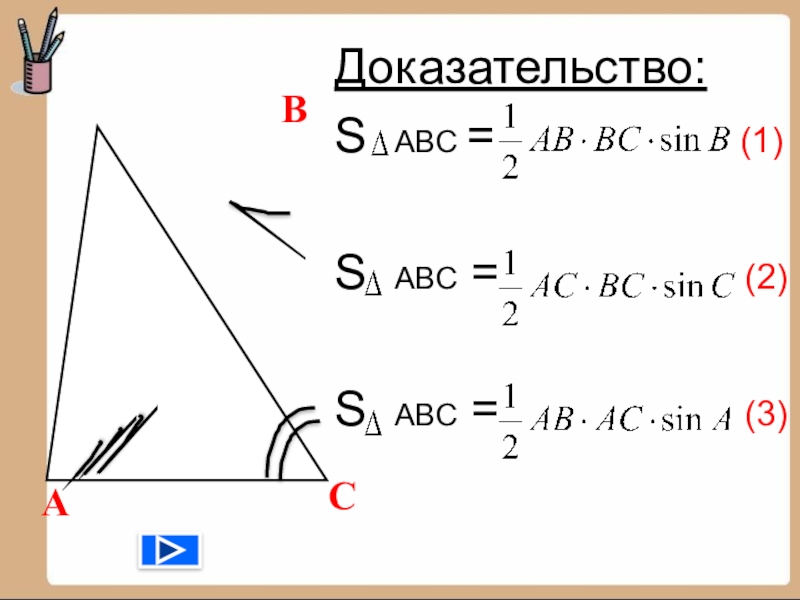
- 12. Доказательство:S ABC =
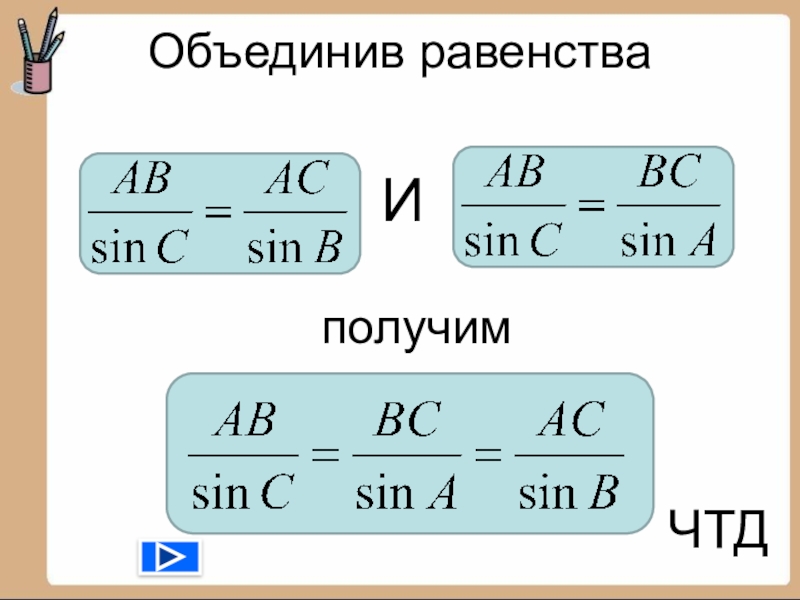
- 13. Приравняем равенства (1) и (2), получим
- 14. Приравняем равенства (2) и (3), получим
- 15. Объединив равенства ИполучимЧТД
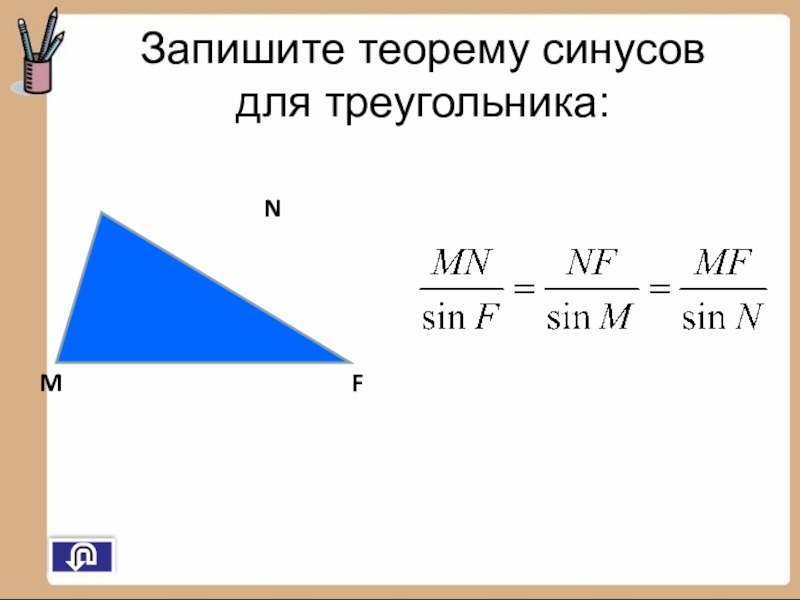
- 16. Запишите теорему синусов для треугольника:MFN
- 17. Теорема косинусовКвадрат длины любой стороны треугольника равен
- 18. АСДано: АВСДоказать:В
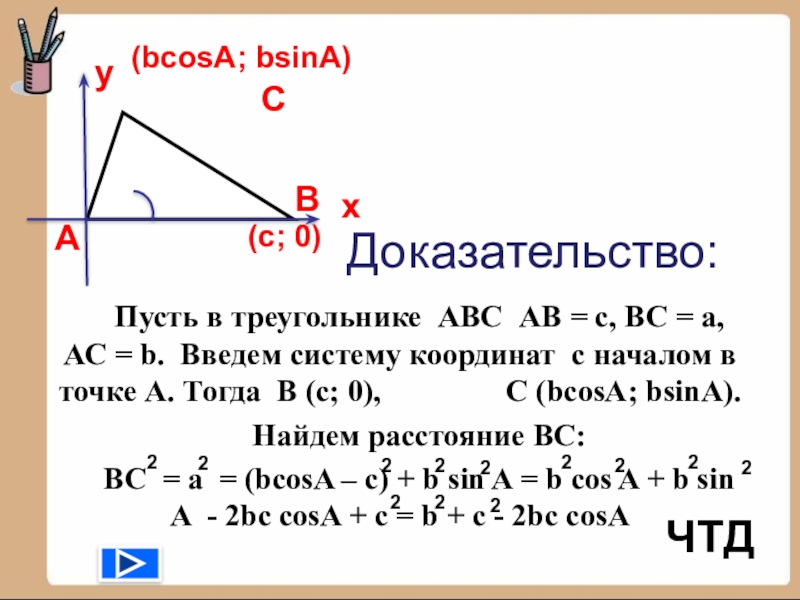
- 19. Пусть в треугольнике АВС АВ = с,
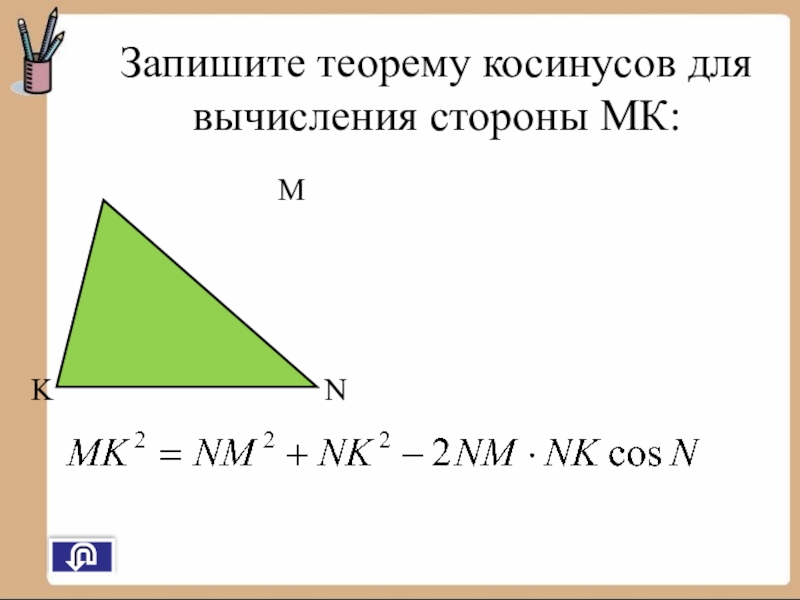
- 20. MNKЗапишите теорему косинусов для вычисления стороны МК:
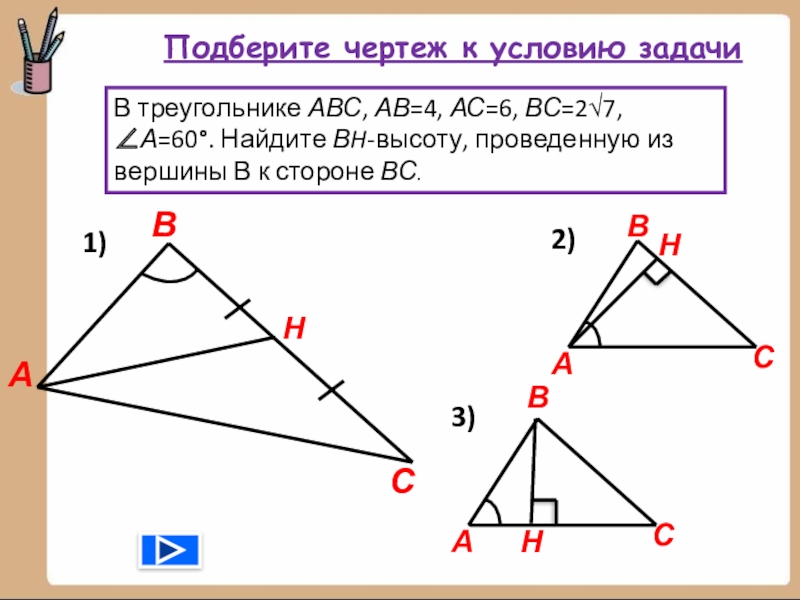
- 21. Подберите чертеж к условию задачиВ треугольнике АВС,
- 22. Решение:Дано:∆ АВС, ∠А=60°,АВ=4, АС=6, ВС=2 .Найти: BH.2)
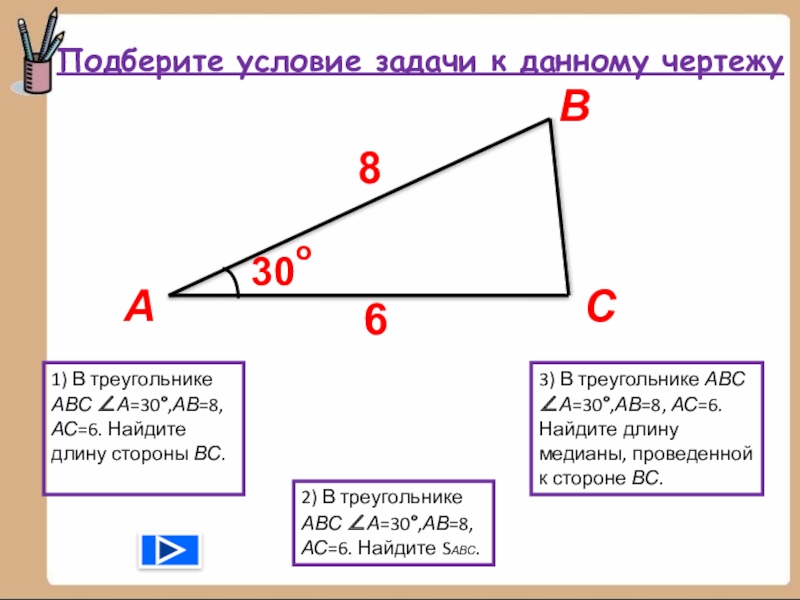
- 23. ВАС8630о1) В треугольнике АВС ∠А=30°,АВ=8, АС=6. Найдите
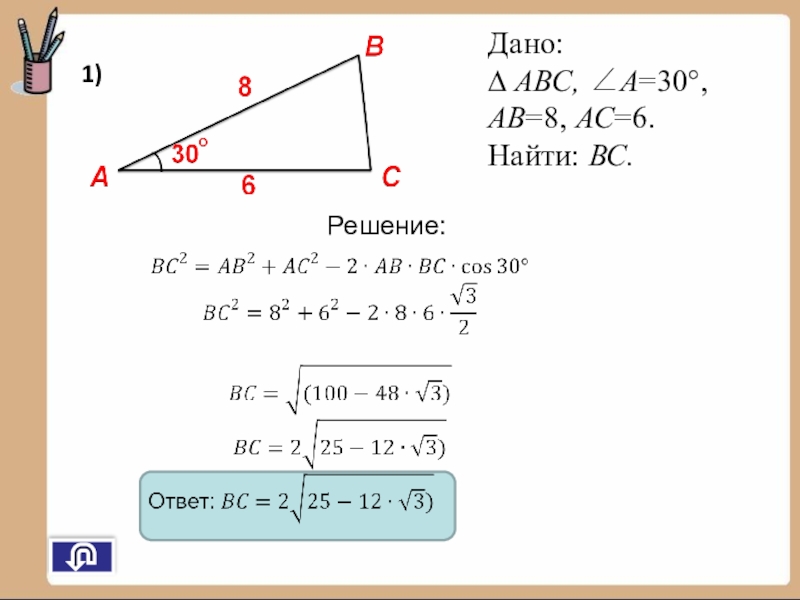
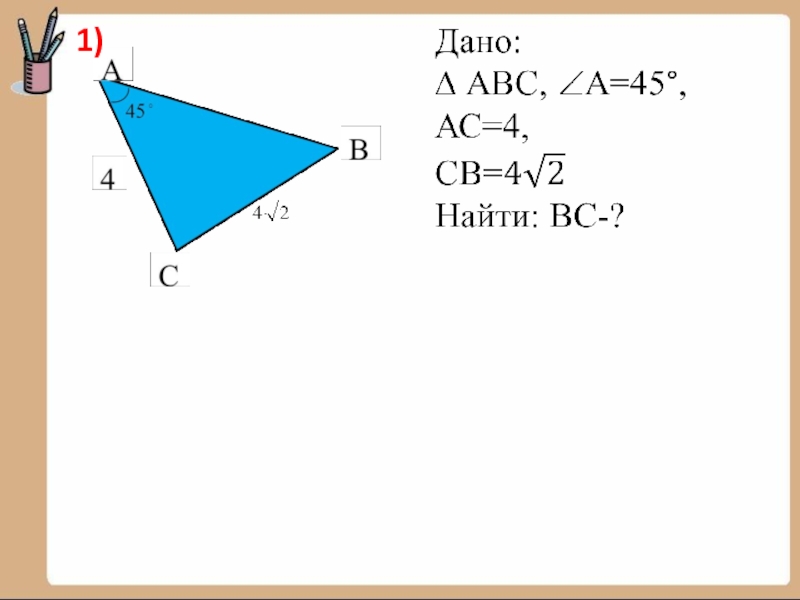
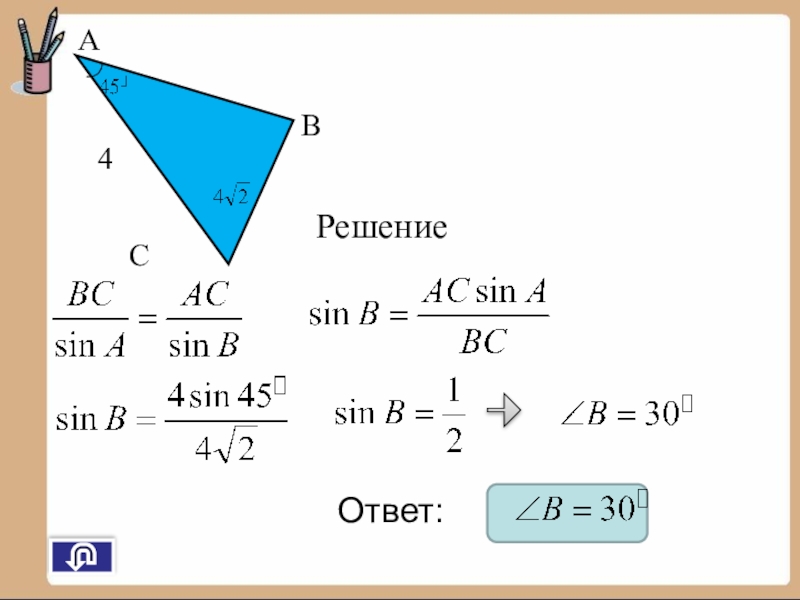
- 24. Дано: ∆ АВС, ∠А=30°,АВ=8, АС=6.Найти: ВС.1)Решение:
- 25. 1)
- 26. РешениеОтвет:
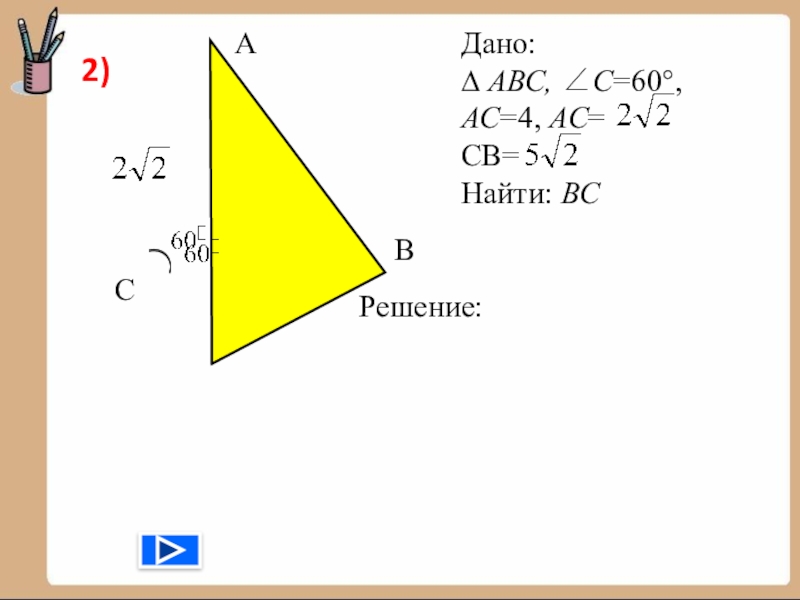
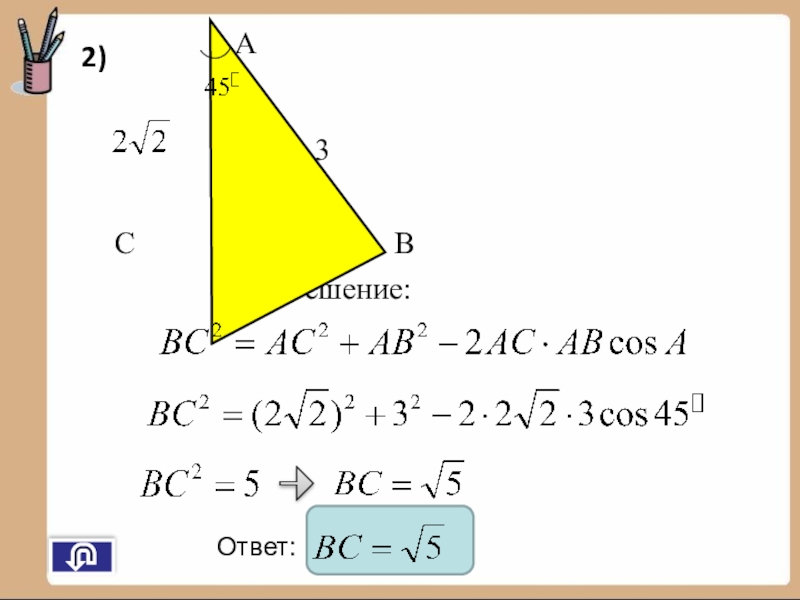
- 27. АСВДано: ∆ АВС, ∠С=60°,АС=4, АС=CB=Найти: ВСРешение:2)
- 28. Решение:АСВ3Ответ: 2)
- 29. Верно ли?а2 = b2 + с2 -
- 30. Верно ли записаны формулировки?1. Квадрат стороны треугольника
- 31. 2. Квадрат стороны треугольника равен сумме квадратов
- 32. 3. Квадрат стороны трапеции равен сумме квадратов
- 33. 4. Квадрат стороны треугольника равен сумме квадратов
- 34. Домашнее задание Знать теорему синусов,
- 35. Слайд 35
- 36. Спасибо за внимание!Среди равных умов при одинаковости прочих условий превосходит тот, кто знает геометрию.Блез Паскаль
Слайд 1Урок по теме:
«Теорема синусов,
Теорема косинусов»
Подготовила
Ищук Ольга Эдуардовна
Геометрия
Слайд 2Цели урока:
1) выработать умения и навыки решения задач, применяя теоремы;
2) показать
3) продолжать развивать внимание, активность, аккуратность, самостоятельность.
Слайд 3План урока:
Повторение
Устные упражнения
Теорема синусов
Теорема косинусов
Практические упражнения
Подберите чертеж
Подберите условие
Решите задачи
Вопросы
Домашнее
Рефлексия
1
2
Слайд 5Сформулируйте теорему о площади треугольника?
Площадь треугольника равна половине произведения двух его
Слайд 17Теорема косинусов
Квадрат длины любой стороны треугольника равен сумме квадратов длин двух
A
B
C
а
с
b
Слайд 19Пусть в треугольнике АВС АВ = с, ВС = а, АС
Найдем расстояние ВС:
ВС = а = (bcosA – c) + b sin A = b cos A + b sin A - 2bc cosA + c = b + c - 2bc cosA
А
С
В
(bcosA; bsinA)
у
х
(с; 0)
Доказательство:
2
2
2
2
2
2
2
2
2
2
2
2
ЧТД
Слайд 21Подберите чертеж к условию задачи
В треугольнике АВС, АВ=4, АС=6, ВС=2√7, ∠А=60°.
А
В
С
Н
А
С
В
Н
1)
2)
А
С
Н
3)
В
Слайд 23В
А
С
8
6
30
о
1) В треугольнике АВС ∠А=30°,АВ=8, АС=6. Найдите длину стороны ВС.
2)
3) В треугольнике АВС ∠А=30°,АВ=8, АС=6. Найдите длину медианы, проведенной к стороне ВС.
Подберите условие задачи к данному чертежу
Слайд 29Верно ли?
а2 = b2 + с2 - 2aс cosC
в2 = с2
с2 = a2 + c2 - 2ab cosA
неверно
верно
неверно
Слайд 30Верно ли записаны формулировки?
1. Квадрат стороны треугольника равен сумме квадратов всех
сторон минус удвоенное произведение любых двух сторон
на косинус угла между ними.
НЕВЕРНО
Слайд 312. Квадрат стороны треугольника равен сумме квадратов двух
других сторон на
НЕВЕРНО
Слайд 323. Квадрат стороны трапеции равен сумме квадратов двух
других сторон минус
косинус угла между ними.
НЕВЕРНО
Слайд 334. Квадрат стороны треугольника равен сумме квадратов двух
других сторон минус
косинус угла между ними.
ВЕРНО
Слайд 34Домашнее задание
Знать теорему синусов, теорему косинусов.
1. Найдите неизвестную сторону треугольника MNP , если MN см, NP = 6 см, а угол N равен 150°.
2. Найдите косинус угла, лежащего против диагонали 14 мм, если стороны параллелограмма равны 8 мм и 10 мм.
Слайд 36Спасибо за внимание!
Среди равных умов при
одинаковости прочих условий превосходит тот,
кто знает геометрию.
Блез Паскаль