Презентация, доклад на тему Схема Горнера и ее применение

Анатольевна

ЕГЭ

0 имеет три различных корня, один из которых х0.

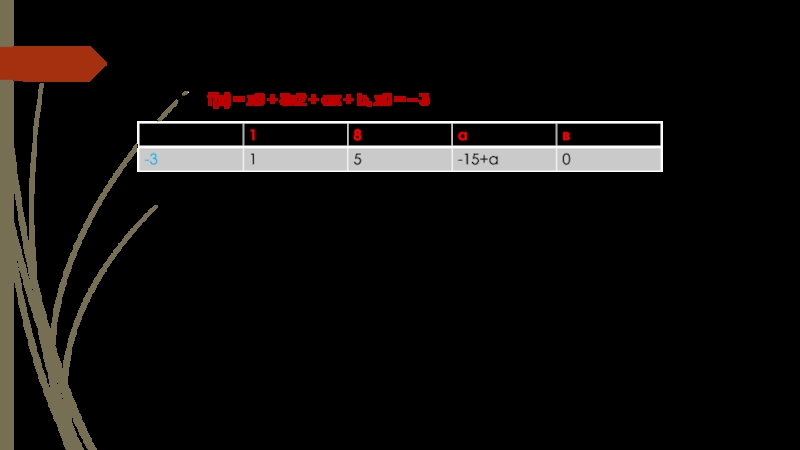
а) f(х) = х3 + 8х2 + ах + b, х0 = – 3




х3 + 8х2 + ах + b = (х + 3) (х2 + 5х + (а – 15))

Уравнение х2 + 5х + (а – 15) = 0 должно иметь два корня. Это выполняется только в том случае, когда D > 0

а = 1; b = 5; с = (а – 15),

D = b2 – 4ac = 25 – 4 (a – 15) = 25 + 60 – 4a > 0,

85 – 4a > 0;

4a < 85;

a < 21,25
Наибольшее целое значение параметра а, при котором уравнение

f(х) = 0 имеет три корня, а = 21

Ответ: 21.

2х2 – 5х + 6=0;
в) 2х4 – 5х3 + 5х2 – 2 = 0;
2. Найдите рациональные корни многочлена
х4 – 2х3 – 8х2 + 13х – 24.
3. Найдите наибольшее целое значение параметра а, при котором уравнение f(х) = 0 имеет три различных корня, один из которых x0.
f(x) = x3 – 2x2 + ax + b, x0 = – 1