Презентация, доклад на тему Сборник задач Текстовые задачи на движение . Подготовка к ОГЭ и ЕГЭ (9 , 11 класс)

учреждение
«Обоянская средняя общеобразовательная школа №2»

МБОУ «Обоянская СОШ №2» города Обояни Курской области

Пособие предназначено для подготовки к ОГЭ по математике, вторая часть (задание №22). В пособии представлены разные задачи на движение повышенной сложности и их способы решения и оформления.

движение типа №22 ОГЭ и №11 ЕГЭ по математике.
На основе решений задач ОГЭ показывается, что во многих случаях для решения таких задач наиболее эффективно применить таблицу при оформлении условия.
В работе рассмотрены решения текстовых задач на движение разного типа.

модуль «Алгебра», 2)модуль «Геометрия». В каждом есть 2 части.
В модуле «Алгебра», во 2 части, меня заинтересовали задачи повышенной сложности №22.
Кроме того, текстовые задачи на движение часто встречаются в ЕГЭ по математике, задачи типа №11
В своём сборнике мы рассмотрим текстовые задачи на движение, различные способы решения и оформления.

либо используются формулы
v=S/t, t=S/v
В качестве переменной x удобно выбрать скорость.
Уравнения составляются по одновременным событиям.
Замечания:
если время события задано, то удобнее составлять уравнение на путь;
если уравнений меньше, чем неизвестных, то нужно ввести в систему искомую величину.

движение одновременно, то до встречи каждое тело затрачивает одинаковое время;
если тела выходят в разное время, то до встречи из них затрачивает время больше то, которое выходит раньше;
в природе скорость расстояние и время положительны.

При решении задач на движение принимают допущения

в голове формулу-ключ, которая связывает путь (расстояние) , скорость и время : s=v·t
Для удобства запоминания создадим свой «дорожный знак»,
который поможет нам найти любой из трех компонентов
S – пройденный путь или расстояние,
V – скорость,
t - время

тело, движется со скоростью v1, догоняет другое, движущегося со скоростью v2 и находящегося от него на расстояние s, то скорость приближения равно v2 - v1,, а время t1, затраченное на то, чтобы догнать будет равно t1=s  
если тела движутся навстречу (при тех же параметрах), то скорость сближения будет равна v1+v2, встретиться же они через t2=s
В случае, когда идет сравнение времени, затраченных на путь различными телами, для правильности уравнения связи этих времен надо посмотреть, какая из величин больше. При составлении уравнения, связывающего эти величины, необходимо ко второй прибавить или от первой отнять положительную величину.

мониторинга качества образования, здесь можно найти Федеральный открытый банк заданий, а также демоверсии заданий ОГЭ и ГВЭ по всем предметам
https://oge.sdamgia.ru — образовательный портал для подготовки к ОГЭ и ГВЭ по 14 предметам! Онлайн тесты и подробное пояснение к задачам и вопросам
http://www.examen.ru — Все о ГИА и ЕГЭ. Онлайн тестирование
http://alexlarin.net – образовательный портал для подготовки к ОГЭ по математике. Онлайн- тестирование. Сборники заданий второй части.
http://www.yaklass.ru – образовательный портал для учащихся 1-11 классов, где можно повторить весь необходимый теоретический материал, а также пройти онлайн - тестирование.

(навстречу и вдогонку, с задержкой в пути);
задачи на движение по замкнутой трассе;
задачи на среднюю скорость;
задачи на движение протяжных тел,
задачи на движение по воде.

уравнение по условию задачи.
Реши уравнение и проверь корни по условию задачи.
Прочитай вопрос к задаче и дай на него ответ.

расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В  на 4 часа позже автомобилиста. Ответ дайте в км/ч. Решение:

50

50

х+40

х

Известно, что велосипедист прибыл в пункт В  на 4 часа позже автомобилиста.
Получим уравнение:

+ 4 =

50х + 4х(х+40) = 50(х+40)
50х+4х² +160х = 50х+2000
4х² +160х – 2000 = 0
х² +40х – 500 = 0
D = 3600; х₁ =10, х2 = - 50
Скорость не может быть отрицательной, следовательно
скорость велосипедиста равна 10 км/ч.
Ответ: 10

Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 85 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 390 км от города A. Ответ дайте в км/ч.

Решение:
Пусть x (км/ч) - скорость первого автомобиля.
Скорость второго автомобиля - 85 км/ч.
Так как автомобили встретились на расстоянии 390 км от города A, то первый автомобиль ехал 390/x часов. Второй автомобиль проехал до встречи
730 - 390 = 340 км.
Время, которое затратил второй автомобиль на дорогу, равно 340/85 = 4 часа.
Так как второй автомобиль выехал на 2 часа позже первого, то первый ехал до встречи на 2 часа дольше.
Составим и решим уравнение: 390/x - 4 = 2,
390/x = 6,
x = 390/6 = 65.
То есть скорость первого автомобиля равна 65 км/ч.
Ответ: 65 км/ч.

Диагностические работы)

навстречу друг другу отправляются два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 6 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 162 км, скорость первого велосипедиста равна 15 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

Решение:
6 мин = 6/60ч = 0,1ч
Пусть х км – расстояние, которое проехал второй велосипедист до встречи, тогда (162-х)км проехал первый велосипедист до встречи.
Время второго велосипедиста до встречи - х/30 ч,
а первого –((162-х)/15+ 0,1) ч.
Составим уравнение х/30=(162-х)/15+0,1 и решим его.
х= 109
Значит, 109 км – искомое расстояние.
Ответ: 109 км.

одновременно отправляются в 60- километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым.

Решение:
Пусть х км/ч - скорость второго велосипедиста, тогда (х+10)км/ч – скорость первого велосипедиста.
60/х ч – время, которое затратил второй велосипедист на пробег,
60/(х+10) – время первого велосипедиста.
Составим уравнение 60/х – 60/(х+10) = 3 и решим его.
Умножим обе части уравнения на х(х+10)‡0.
После преобразований имеем уравнение х² +10х -200 = 0.
Корни уравнения 10 и -20(не подходит по условию).
Значит, 10 км/ч скорость велосипедиста, пришедшего вторым.
Ответ: 10 км/ч.

скоростью 56 км/ч, а вторую — со скоростью 84 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Нахождение средней скорости

ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение. Средняя скорость — это все пройденное расстояние, разделённое на все затраченное время движения.
Первый отрезок пути автомобиль проехал за 300/6 = 5 часов, второй — за 300/100 = 3 часа,
третий — за 300/75 = 4 часа.
Средняя скорость автомобиля на протяжении всего пути составила 
 
Ответ: 75км/ч.

направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 70 км/ч и 30 км/ч. Длина товарного поезда равна 1400 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

70-30=40(км/ч) – скорость сближения поездов
40 км/ч = 40 ·1000:60 м/мин = 2000/3 м/мин.
3·2000/3= 2000(м) – проедет пассажирский поезд за 3 минуты, это расстояние равно сумме длин поездов.
2000 – 1400 = 600(м) – длина пассажирского поезда
Ответ: 600 метров.

проезжает мимо идущего параллельно путям со скоростью 6 км/ч навстречу ему пешехода за 30 секунд. Найдите длину поезда в метрах.

Решение:
54+6=60 (км/ч) скорость сближения
60 км/ч = 60·1000:60 м/мин
30 сек. = 0,5 мин
1000·0,5 = 500 (м) длина поезда.
Ответ: 500 м.

данным задачи с учетом движения по течению и против течения.
Составь уравнение по условию задачи.
Реши уравнение и проверь корни по условию задачи.
Прочитай вопрос к задаче и дай на него ответ.

скорость лодки по течению реки,
(х-4)км/ч – скорость лодки против течения реки.
77/(х-4)ч – время лодки против течения реки,
77/(х-4)ч – время по течению реки, на 2ч меньше
Составим уравнение 77/(х-4) – 77(х+4) = 2 и решим его. х=18
Значит, собственная скорость лодки 18 км/ч.
Ответ: 18 КМ/Ч

Движение по воде № 8. Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.

Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 3,5 км от места отправления. Один идет со скоростью 2,7 км/ч, а другой — со скоростью 3,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
2) Дорога между пунктами A и B состоит из подъёма и спуска, а её длина равна 19 км. Турист прошёл путь из A в B за 5 часов, из которых спуск занял 4 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?
3) Из двух городов одновременно навстречу друг другу отправляются два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 6 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 162 км, скорость первого велосипедиста равна 15 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
4) Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.
5) От пристани A к пристани B, расстояние между которым равно 70 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно.

Два автомобиля отправляются в 340-километровый пробег. Первый едет со скоростью на 17 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
7) Из A в B одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в результате чего прибыл в B одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 40 км/ч.
8) Велосипедист выехал с постоянной скоростью из города А в город B, расстояние между которыми равно 60 км. Отдохнув, он отправился обратно в A, увеличив скорость на 10 км/ч. По пути он сделал остановку на 3 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B.
9) Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым.
10) Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.

11) Из городов A и B навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 2 часа раньше, чем велосипедист приехал в A, а встретились они через 45 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
12) Расстояние между городами A и B равно 80 км. Из города A в город B выехал автомобиль, а через 20 минут следом за ним со скоростью 90 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе C и повернул обратно. Когда он проехал половину пути из C в A, автомобиль прибыл в B. Найдите расстояние от A до C.
13) Первый велосипедист выехал из посёлка по шоссе со скоростью 12 км/ч. Через час после него со скоростью 10 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа после этого догнал первого.
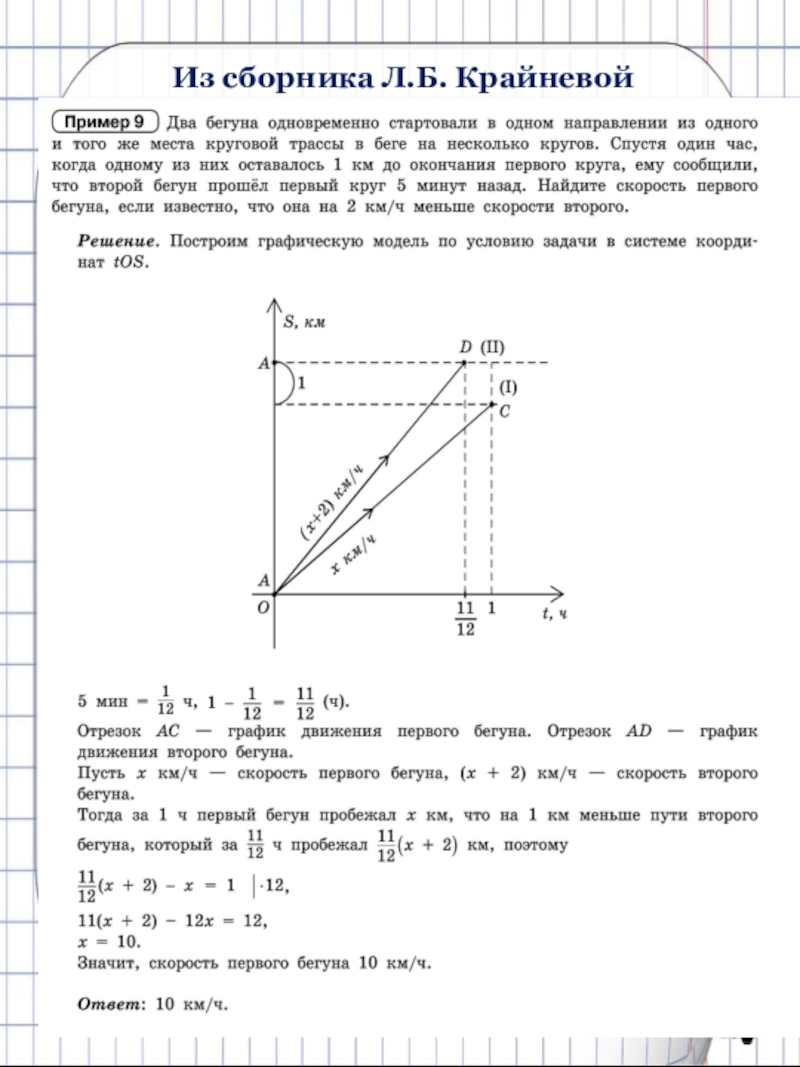
14) Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 5 минут назад. Найдите скорость первого бегуна, если известно, что она на 2 км/ч меньше скорости второго.
15) Расстояние между пристанями A и B равно 60 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошёл 36 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.

16) Первые 2 часа автомобиль ехал со скоростью 55 км/ч, следующий час — со скоростью 70 км/ч, а последние 3 часа — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
17) Первые 100 км автомобиль ехал со скоростью 50 км/ч, следующие 240 км — со скоростью 60 км/ч, а последние 200 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
18) Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найдите длину поезда в метрах.
19) Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает мимо идущего параллельно путям со скоростью 6 км/ч навстречу ему пешехода за 30 секунд. Найдите длину поезда в метрах.
20) Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.
21) По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 70 км/ч и 30 км/ч. Длина товарного поезда равна 1400 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.

При движении по реке:
Скорость по течению = собственная скорость транспорта + скорость течения реки
Скорость против течения = собственная скорость транспорта - скорость течения реки

– М.: Издательство «Экзамен», 2018. -96с. (Серия «ОГЭ. Типовые тестовые задания»), 2018.
Л.Б. Крайнева. Задания повышенного и высокого уровней сложности. ОГЭ 2018. М.: Бином. Лаборатория знаний. Редакция «Поколение V», 2018.
Семенов А.Л, Ященко И.В. ОГЭ 2017. Математика. Универсальные материалы для подготовки учащихся. М.: Интеллект-Центр, 2017.
А.Л. Семенов, И.В. Ященко. ОГЭ-2016. Математика: типовые экзаменационные варианты: 30 вариантов. М.: Национальное образование, 2016.
Библиотечка СтатГрада. Математика. Подготовка к ОГЭ в 2017году. Диагностические работы. — М.: МЦНМО, 2017.
Шевкин А.В. Текстовые задачи в школьном курсе математики : лекции/ А.В.Шевкин – М. : Педагогический университет «Первое сентября», 2006
Смирнов С. Решение задач на движение : http:// www.egesdam.ru
https://math-oge.sdamgia.ru
https://www.yaklass.ru
https://statgrad.org
https:// www.fipi.ru