- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задания №23 ОГЭ по математике Построение графиков функций
Содержание
- 1. Решение задания №23 ОГЭ по математике Построение графиков функций
- 2. Для решения данных заданий необходимо уметь:- выполнять
- 3. Сайт http://alexlarin.net/
- 4. Пример 1 (ОГЭ-2016)Построить график функции и
- 5. 2. Преобразуем полученную функцию, а также уточним
- 6. Слайд 6
- 7. 4. Приступаем ко второй части задачи. Необходимо
- 8. Слайд 8
- 9. Как мы видим, разным цветом показаны прямые
- 10. Уравнение той части параболы, где прямая имеет
- 11. Пример 2 (демо-2017).
- 12. Решение.1. Область определения данной дробно-рациональной функции –
- 13. Слайд 13
- 14. Слайд 14
- 15. Приступим ко второму заданию: найдем точки пересечения
- 16. P.S. Какие знания и умения мы использовали
Для решения данных заданий необходимо уметь:- выполнять преобразования алгебраических выражений, -решать уравнения, неравенства и их системы, - строить и читать графики функций, - разрабатывать и исследовать простейшие математические модели.
Слайд 1Решение задания №23
ГИА по математике
«Построение графиков функций»
Автор
Марченко Т.Н.,
учитель математики
г. Светлоград,
МБОУЛ №3
Слайд 2Для решения данных заданий необходимо уметь:
- выполнять преобразования алгебраических выражений,
-решать
уравнения, неравенства и их системы,
- строить и читать графики функций,
- разрабатывать и исследовать простейшие математические модели.
- строить и читать графики функций,
- разрабатывать и исследовать простейшие математические модели.
Слайд 4Пример 1 (ОГЭ-2016)
Построить график функции
и определить, при каких
a прямая y=ax имеет с
графиком ровно две общие точки.
Решение.
Раскроем модуль в соответствии с его
определением:
графиком ровно две общие точки.
Решение.
Раскроем модуль в соответствии с его
определением:
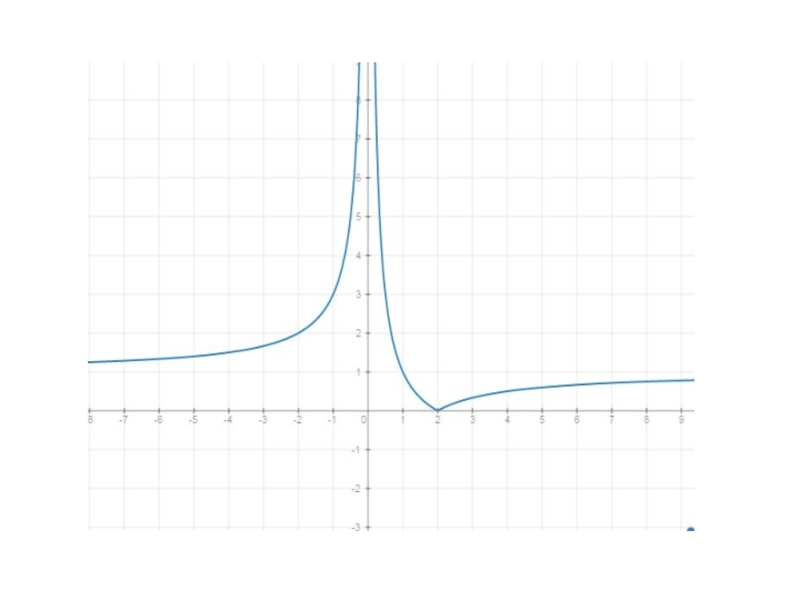
Слайд 52. Преобразуем полученную функцию, а также уточним область определения:
Таким образом, на
различных интервалах изменения переменной x видим две смещенные гиперболы.
3. Строим график. Здесь воспользуемся построителем http://easyto.me/
3. Строим график. Здесь воспользуемся построителем http://easyto.me/
Слайд 74. Приступаем ко второй части задачи. Необходимо найти точки пересечения данной
кусочной функции с прямой y=ax.
Такая прямая, вне зависимости от знака углового коэффициента, проходит через начало координат, то есть т. О(0,0). Мы можем провести несколько таких прямых и понаблюдать, сколько точек пересечения может быть у гипербол и данной прямой в зависимости от коэффициента a.
Воспользуемся http://easyto.me/
Такая прямая, вне зависимости от знака углового коэффициента, проходит через начало координат, то есть т. О(0,0). Мы можем провести несколько таких прямых и понаблюдать, сколько точек пересечения может быть у гипербол и данной прямой в зависимости от коэффициента a.
Воспользуемся http://easyto.me/
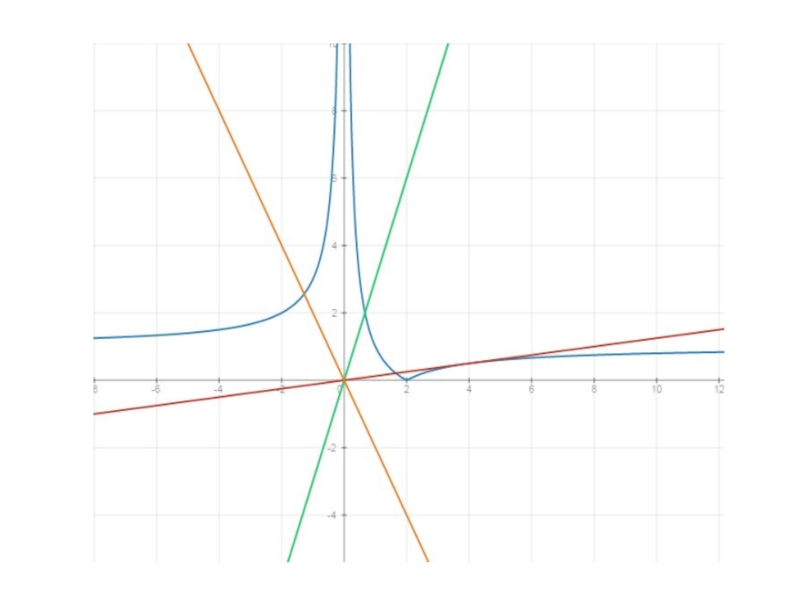
Слайд 9Как мы видим, разным цветом показаны прямые с разным угловым коэффициентом.
Только в одном положении прямая (на рисунке она изображена красным) имеет две общие точки с гиперболой: одну ветку прямая пересекает, а другой касается. В 11 классе мы бы могли воспользоваться производной функции для нахождения точки касания. Но можно решить задачу, пользуясь имеющимися в 9 классе знаниями.
Слайд 10Уравнение той части параболы, где прямая имеет ровно одну общую точку,
Запишем систему:
Далее приравняем правые части:
Слайд 12Решение.
1. Область определения данной дробно-рациональной функции – вся числовая ось, кроме
корней знаменателя, а именно точек x=3 и x=-2.
Преобразуем функцию, приведем ее к какому-нибудь знакомому виду уравнения линии.
Выпишем числитель, решим биквадратное уравнение, разложим числитель на множители.
Преобразуем функцию, приведем ее к какому-нибудь знакомому виду уравнения линии.
Выпишем числитель, решим биквадратное уравнение, разложим числитель на множители.
Слайд 15
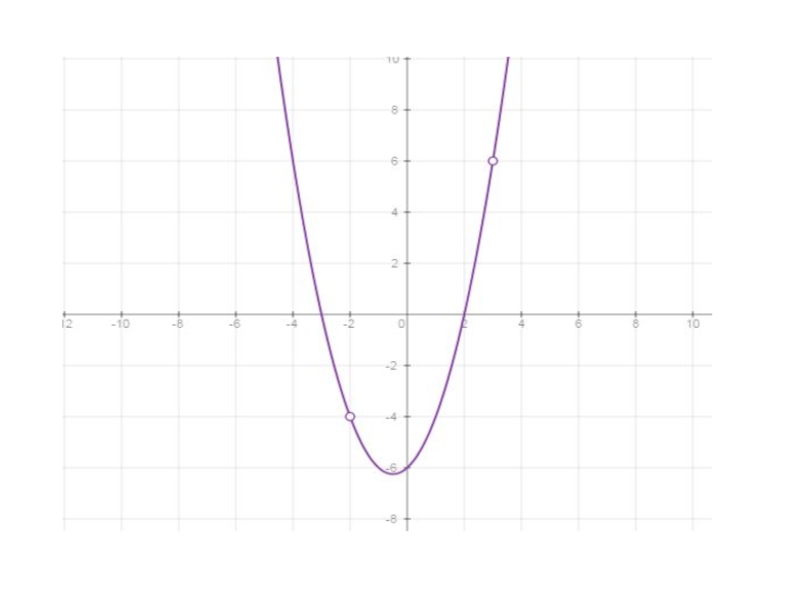
Приступим ко второму заданию: найдем точки пересечения прямой y=c c
параболой.
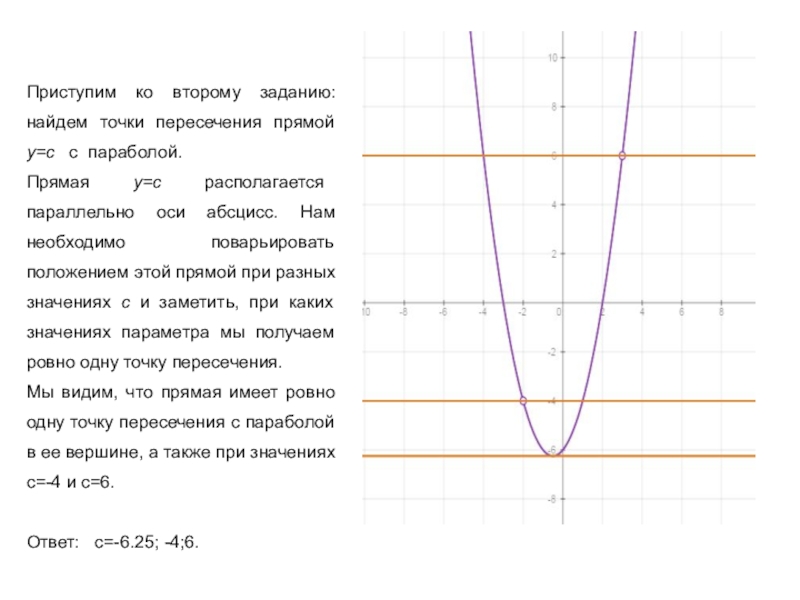
Прямая y=c располагается параллельно оси абсцисс. Нам необходимо поварьировать положением этой прямой при разных значениях с и заметить, при каких значениях параметра мы получаем ровно одну точку пересечения.
Мы видим, что прямая имеет ровно одну точку пересечения с параболой в ее вершине, а также при значениях с=-4 и с=6.
Ответ: с=-6.25; -4;6.
Прямая y=c располагается параллельно оси абсцисс. Нам необходимо поварьировать положением этой прямой при разных значениях с и заметить, при каких значениях параметра мы получаем ровно одну точку пересечения.
Мы видим, что прямая имеет ровно одну точку пересечения с параболой в ее вершине, а также при значениях с=-4 и с=6.
Ответ: с=-6.25; -4;6.
Слайд 16P.S. Какие знания и умения мы использовали для решения данных задач?
-
Определение модуля;
- решение неравенств методом интервалов;
- знание уравнений и графиков функций, умение их строить;
- понимание понятия «область определения функции»;
- умение решать системы и квадратные уравнения, а также понимание,
с какой целью мы их используем;
- а также общемыслительные логические и аналитические умения,
умение рассуждать, варьировать данными, делать выводы.
- решение неравенств методом интервалов;
- знание уравнений и графиков функций, умение их строить;
- понимание понятия «область определения функции»;
- умение решать системы и квадратные уравнения, а также понимание,
с какой целью мы их используем;
- а также общемыслительные логические и аналитические умения,
умение рассуждать, варьировать данными, делать выводы.