- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач с помощью систем уравнений 2 часть 7 класс
Содержание
- 1. Решение задач с помощью систем уравнений 2 часть 7 класс
- 2. 120увеличилось на 40%уменьшилось на 10%стало > на 30
- 3. Решение:Пусть х лошадей было в первом табуне,
- 4. х + у = 1201,4х - 0,9у = 30
- 5. х + у = 1201,4х - 0,9у
- 6. х + у = 1201,4х - 0,9у
- 7. х + у = 1201,4х - 0,9у
- 8. х + у = 1201,4х - 0,9у
- 9. х + у = 1201,4х - 0,9у
- 10. х + у = 1201,4х - 0,9у
- 11. Слайд 11
- 12. Пусть х км/ - скорость первого
- 13. 2х + 2у = 44 2х - 2у = 4
- 14. 2х + 2у = 44 2х
- 15. 2х + 2у = 44 2х
120увеличилось на 40%уменьшилось на 10%стало > на 30
Слайд 3Решение:
Пусть х лошадей было в первом табуне,
у лошадей было во
втором табуне.
140% = 1,4 90% = 0,9
По условию задачи сумма х и у равна 120, разность 1,4х и 0,9у равна 30.
140% = 1,4 90% = 0,9
По условию задачи сумма х и у равна 120, разность 1,4х и 0,9у равна 30.
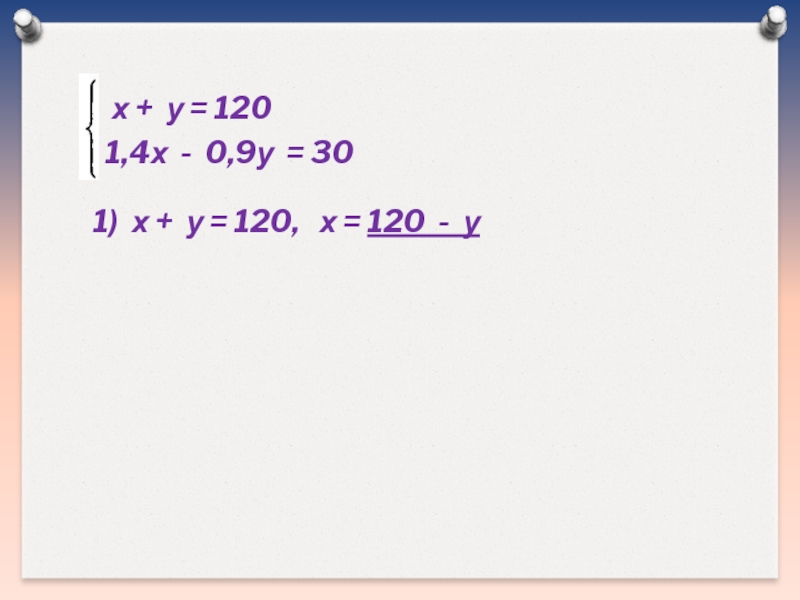
Слайд 7х + у = 120
1,4х - 0,9у = 30
1)
х + у = 120, х = 120 - у
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
Слайд 8х + у = 120
1,4х - 0,9у = 30
1)
х + у = 120, х = 120 - у
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
-2,3у = - 138 1380 : 23 = 60
х = 60
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
-2,3у = - 138 1380 : 23 = 60
х = 60
Слайд 9х + у = 120
1,4х - 0,9у = 30
1)
х + у = 120, х = 120 - у
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
-2,3у = - 138 1380 : 23 = 60
х = 60
У = 120 - 60
у = 60
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
-2,3у = - 138 1380 : 23 = 60
х = 60
У = 120 - 60
у = 60
Слайд 10х + у = 120
1,4х - 0,9у = 30
1)
х + у = 120, х = 120 - у
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
-2,3у = - 138 1380 : 23 = 60
х = 60
У = 120 - 60
у = 60
Ответ: в первом табуне было 60 лошадей,
во втором табуне было 60 лошадей.
2) 1,4 · (120 - у) - 0,9у = 30
168 - 1,4у - 0,9у = 30
- 2,3у = 30 – 168
-2,3у = - 138 1380 : 23 = 60
х = 60
У = 120 - 60
у = 60
Ответ: в первом табуне было 60 лошадей,
во втором табуне было 60 лошадей.
Слайд 12Пусть х км/ - скорость первого всадника,
у км/ч - скорость
второго всадника.
По условию задачи сумма 2х и 2у равна 44, разность
2х и 2у равна 4.
По условию задачи сумма 2х и 2у равна 44, разность
2х и 2у равна 4.
2х + 2у = 44
2х - 2у = 4
Слайд 14 2х + 2у = 44
2х - 2у = 4
1)
_ 2х + 2у = 44 2) 2х + 2 · 10 = 44
2х – 2у = 4 2х = 44 - 20
--------------------------------------------- 2х = 24
2у - ( - 2у) = 44 - 4 х = 24 : 2
4у = 40 х = 12
у = 10
2х – 2у = 4 2х = 44 - 20
--------------------------------------------- 2х = 24
2у - ( - 2у) = 44 - 4 х = 24 : 2
4у = 40 х = 12
у = 10
Слайд 15 2х + 2у = 44
2х - 2у = 4
1)
_ 2х + 2у = 44 2) 2х + 2 · 10 = 44
2х – 2у = 4 2х = 44 - 20
--------------------------------------------- 2х = 24
2у - ( - 2у) = 44 - 4 х = 24 : 2
4у = 40 х = 12
у = 10
Ответ: скорость первого всадника равна 12 км/ч,
. скорость второго всадника равна 10 км/ч
2х – 2у = 4 2х = 44 - 20
--------------------------------------------- 2х = 24
2у - ( - 2у) = 44 - 4 х = 24 : 2
4у = 40 х = 12
у = 10
Ответ: скорость первого всадника равна 12 км/ч,
. скорость второго всадника равна 10 км/ч