- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение задач на растворы, смеси и сплавы
Содержание
- 1. Решение задач на растворы, смеси и сплавы
- 2. Задача 1. В сосуд содержащий 2 кг
- 3. Задача 2.Сколько нужно добавить воды в сосуд,
- 4. Задача 3. Смешали некоторое количество 12% раствора
- 5. Задача 4. Смешали 8кг 18 % раствора
- 6. Задача 5 Смешав 40 % и 15
- 7. Итак, 0,4х + 0,15у + 0,8·3 =
- 8. Задача 6. Имеется три сосуда. В первый
- 9. Итак, получаем систему уравнений :Решаем её:Ответ :1,5 кг сахарного сиропа 15 % концентрации.
- 10. Задача 7 Одна смесь содержит вещества А
- 11. По условию задачи А :В = 5
- 12. Задача 8. Имеются два сплава, состоящие из
- 13. ·121 =
- 14. Задача 9.Из полного бака, содержащего 256 кг
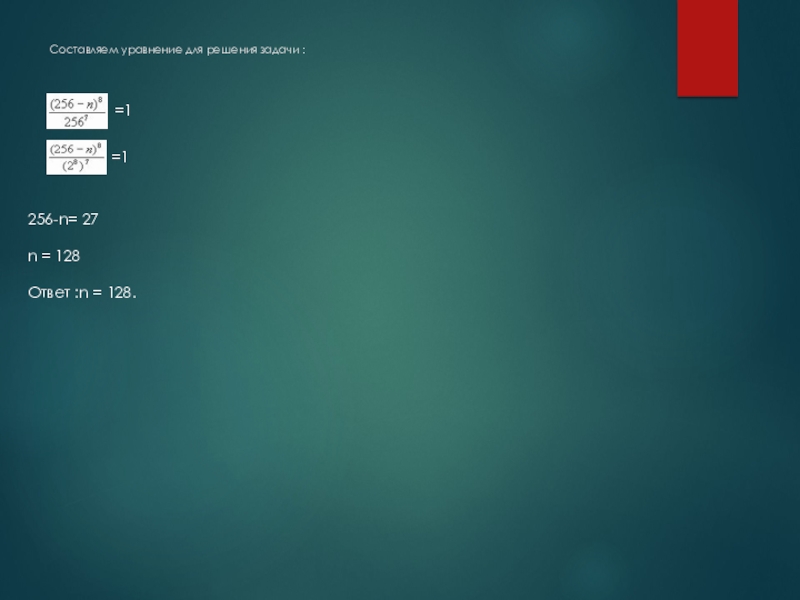
- 15. Составляем уравнение для решения задачи :
Слайд 1Задачи на растворы, смеси и сплавы
Подготовила:
Казанцева Елена 9 а класс
МКОУ «Гончаровская
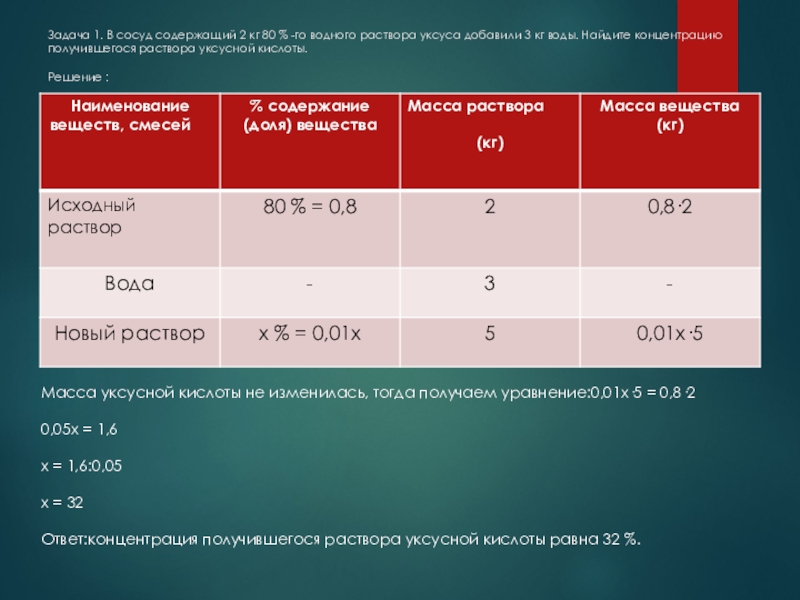
Слайд 2Задача 1. В сосуд содержащий 2 кг 80 % -го водного
Масса уксусной кислоты не изменилась, тогда получаем уравнение:0,01х·5 = 0,8·2
0,05х = 1,6
х = 1,6:0,05
х = 32
Ответ:концентрация получившегося раствора уксусной кислоты равна 32 %.
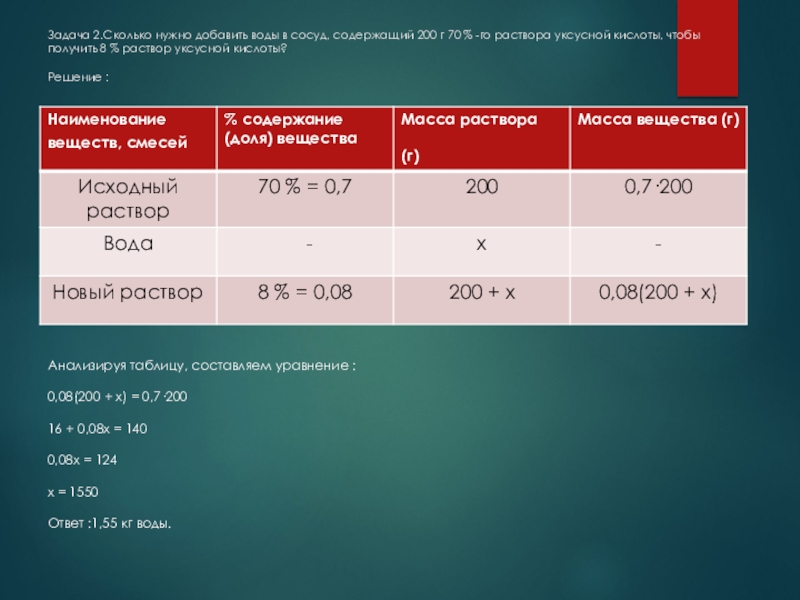
Слайд 3Задача 2.Сколько нужно добавить воды в сосуд, содержащий 200 г 70
Анализируя таблицу, составляем уравнение :
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ :1,55 кг воды.
Слайд 4Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким
Анализируя таблицу, составляем уравнение :
0,12у + 0,2у = 0,01х·2у
Получили уравнение с двумя переменными, учитывая, что Y не равно 0, имеем
0,32 = 0,02х
х = 16
Ответ :концентрация раствора 16 %.
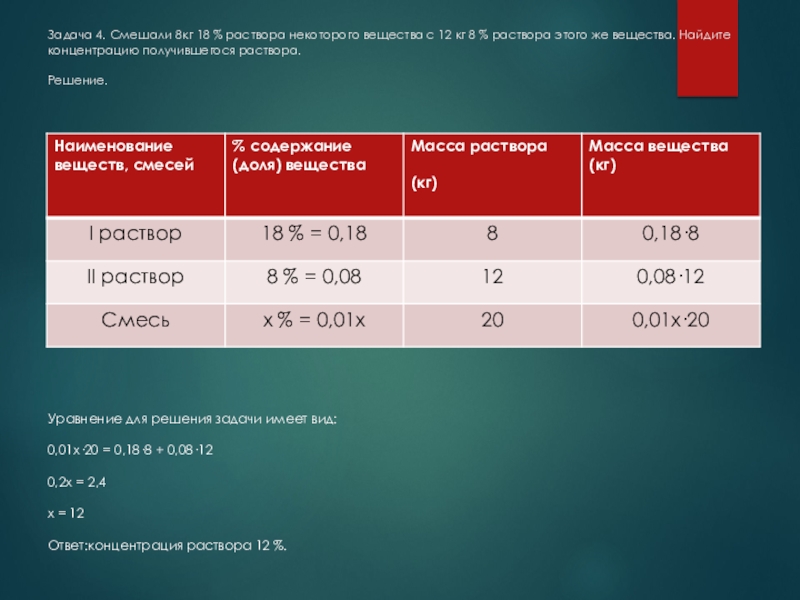
Слайд 5Задача 4. Смешали 8кг 18 % раствора некоторого вещества с 12
Уравнение для решения задачи имеет вид:
0,01х·20 = 0,18·8 + 0,08·12
0,2х = 2,4
х = 12
Ответ:концентрация раствора 12 %.
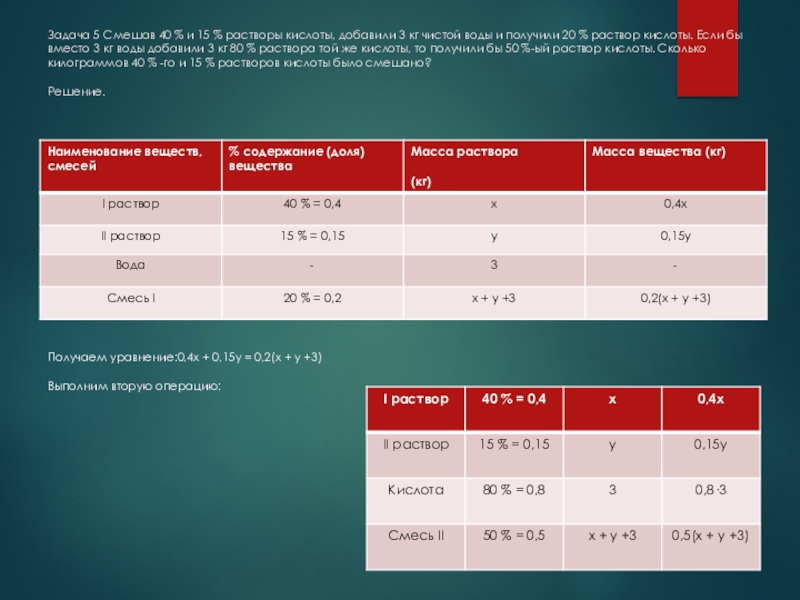
Слайд 6Задача 5 Смешав 40 % и 15 % растворы кислоты, добавили
Получаем уравнение:0,4х + 0,15у = 0,2(х + у +3)
Выполним вторую операцию:
Слайд 7Итак, 0,4х + 0,15у + 0,8·3 = 0,5(х + у +3). Для
Решаем систему уравнений:
Ответ:3,4 кг 40 % кислоты и 1,6 кг 15 % кислоты.
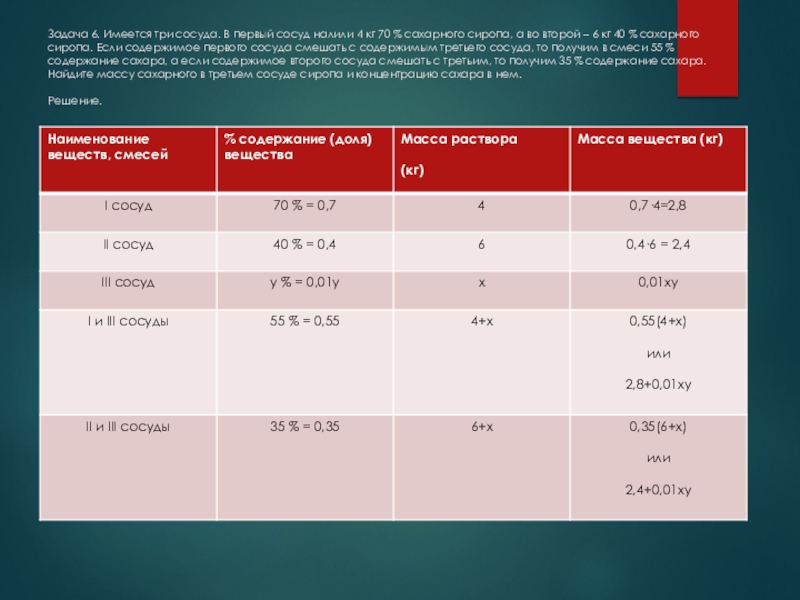
Слайд 8Задача 6. Имеется три сосуда. В первый сосуд налили 4 кг
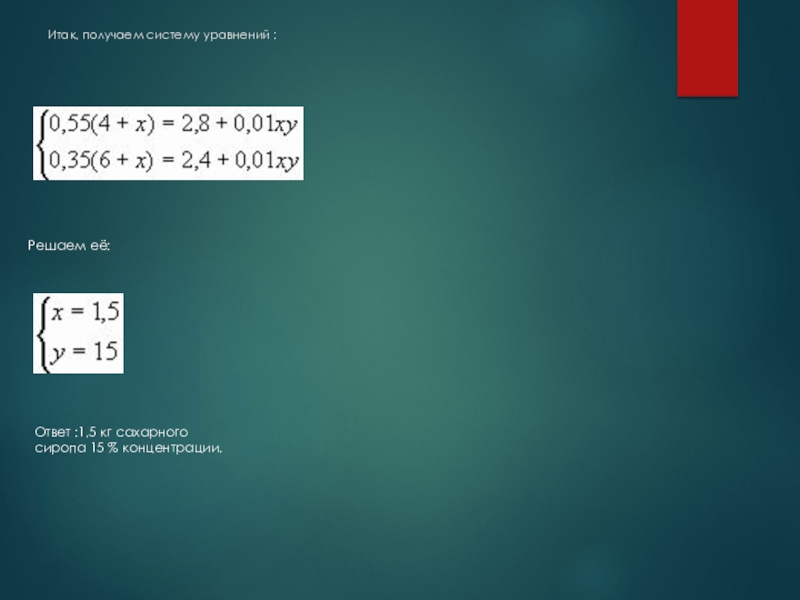
Слайд 9Итак, получаем систему уравнений :
Решаем её:
Ответ :1,5 кг сахарного сиропа 15
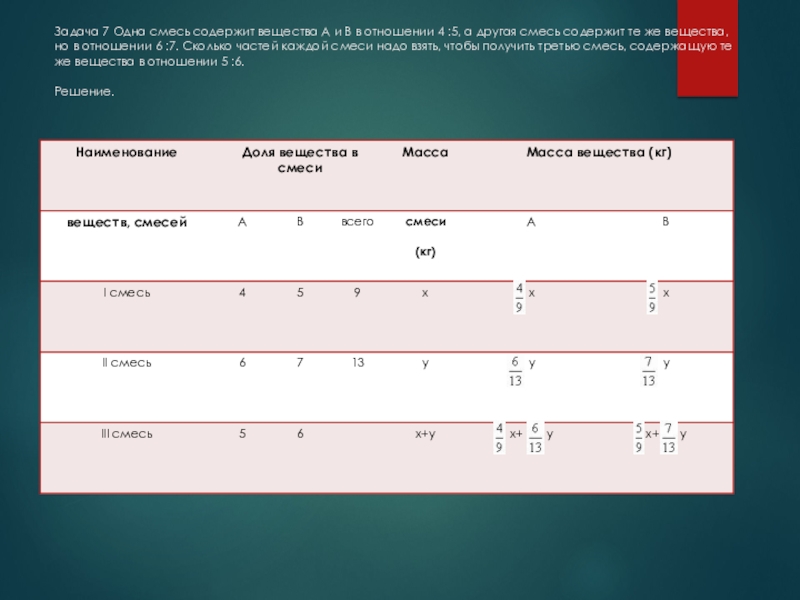
Слайд 10Задача 7 Одна смесь содержит вещества А и В в отношении
Слайд 11По условию задачи А :В = 5 :6, тогда
В данном случае
Решаем уравнение относительно
Получим =
Ответ : 9 частей первой смеси и 13 частей второй смеси.
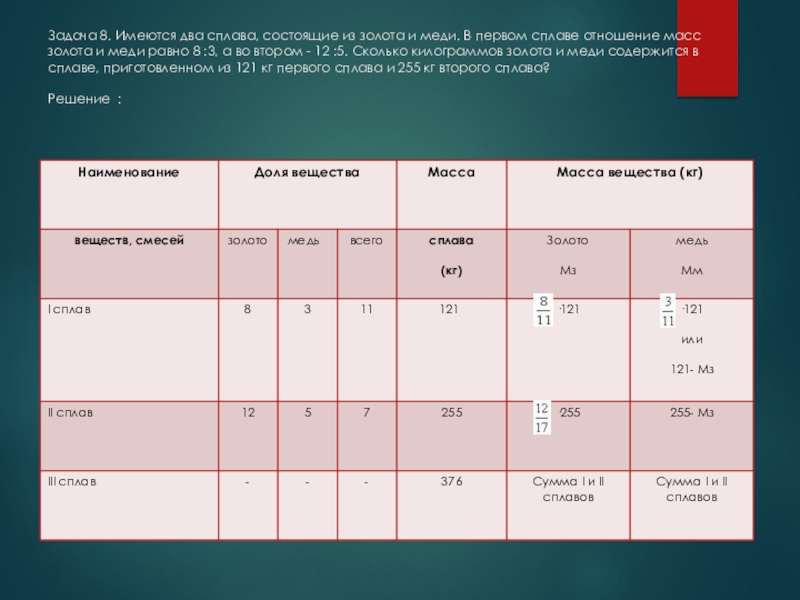
Слайд 12Задача 8. Имеются два сплава, состоящие из золота и меди. В
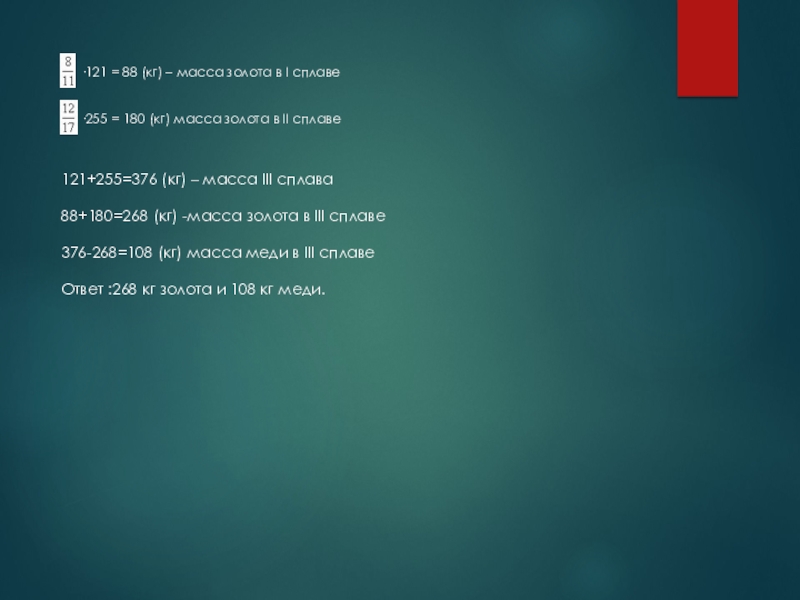
Слайд 13 ·121 = 88 (кг) – масса
·255 = 180 (кг) масса золота в II сплаве
121+255=376 (кг) – масса III сплава
88+180=268 (кг) -масса золота в III сплаве
376-268=108 (кг) масса меди в III сплаве
Ответ :268 кг золота и 108 кг меди.