- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение неравенств второй степени с одной переменной
Содержание
- 1. Решение неравенств второй степени с одной переменной
- 2. еванреонвтс, ерокнь, таиимдкисрнн, ргафки Неравенство, корень, дискриминант, график
- 3. Решение неравенств второй степени с одной переменной
- 4. у(х)"Реши сам-помоги товарищу!"Девиз урока:
- 5. «5»- 5 верных заданий«4»- 4 верных задания«3»- 3 верных задания.5243Проверка домашнего задания
- 6. 1. Находим D квадратного трёхчлена и
- 7. 3. Схематично изображаем данный график; -120хуху04. Находим
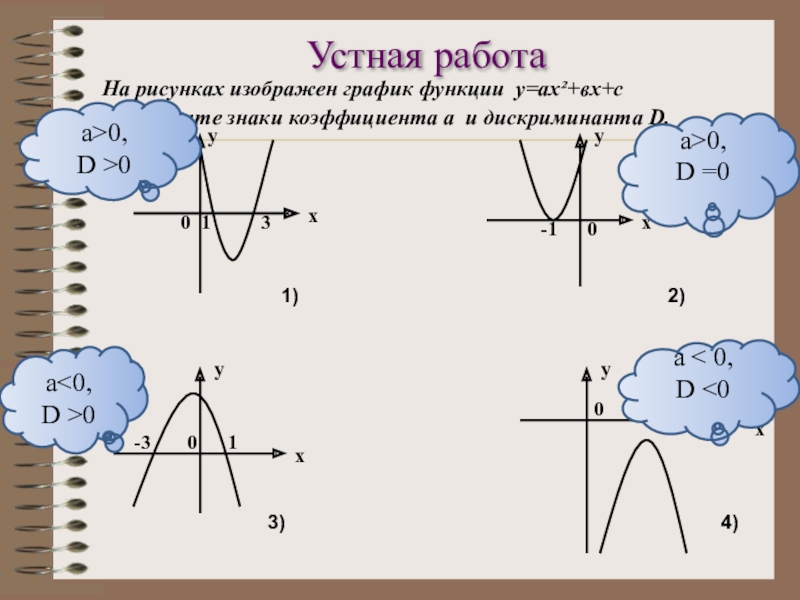
- 8. 1)2)3)4)13ху0-10ху-310ху03хуа0а < 0,D 0,D >0а>0,D =0Устная работа
- 9. Назовите значения переменной х, при которых данная
- 10. Работа в группах
- 11. Слайд 11
- 12. х²-4>0
- 13. Работа в группах (конкурсные задания)
- 14. Проверка решения(-∞;-3)U(3;+ ∞)(0;2)Нет решений[-3;2](-∞;-4)U(1;+ ∞)[1;2]( ;4)(-∞; ∞)(-∞; ]U[1;+ ∞)
- 15. §6, п. 14, №304, №308 а, б, в, №312 а,бДомашнее задание
- 16. Спасибо за урок!
- 17. Список литературы1. Ковалева С.П. Алгебра 9 класс
Слайд 5«5»- 5 верных заданий
«4»- 4 верных задания
«3»- 3 верных задания.
5
2
4
3
Проверка домашнего
Слайд 6 1. Находим D квадратного трёхчлена и выясняем, имеет ли трёхчлен
Решить неравенство
х²-х-2>0 D=(-1)²-4∙1∙(-2)=1+8=9,
D >0, значит квадратный
трёхчлен имеет два корня.
Решить неравенство
х²-х+2<0
D=(-1)²-4∙1∙2=1-8= -7,
D <0, значит квадратный
трёхчлен не имеет корней.
2. Определяемся с местоположением графика квадратичной функции относительно оси ОХ.
Парабола пересекает ось х в двух точках, абсциссы которых равны -1; 2.
Парабола не имеет общих точек с осью х.
Алгоритм решения неравенства
Слайд 73. Схематично изображаем данный график;
-1
2
0
х
у
х
у
0
4. Находим на оси Х промежутки ,
(если решают неравенство ax²+ bx +c >0 ) или ниже оси Х (если решают неравенство ax²+bx+c<0)
(-∞;-1)U(2;+∞)
нет решений
Слайд 8
1)
2)
3)
4)
1
3
х
у
0
-1
0
х
у
-3
1
0
х
у
0
3
х
у
а0
а < 0,
D
а>0,
D >0
а>0,
D =0
Устная работа
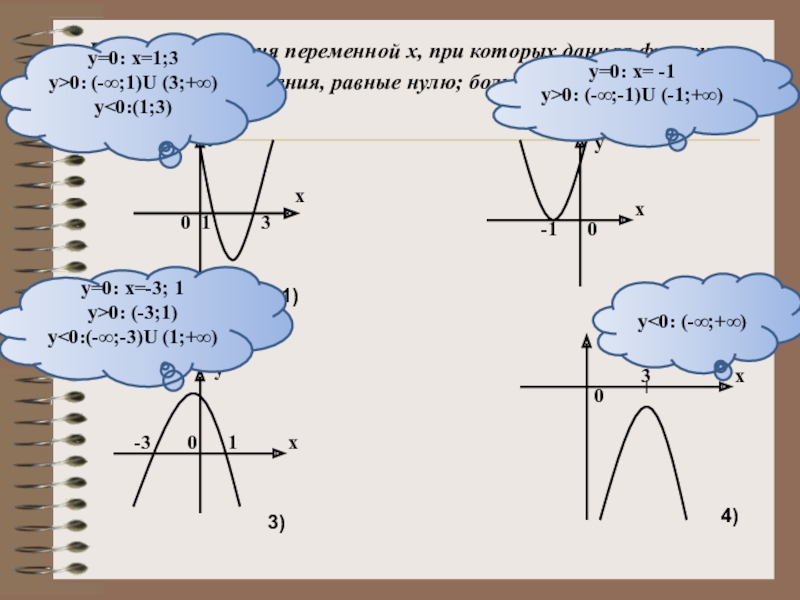
Слайд 9Назовите значения переменной х, при которых данная функция:
а) принимает значения,
1)
2)
3)
4)
1
3
х
у
0
-1
0
х
у
-3
1
0
х
у
0
3
х
у
у=0: х=1;3
у>0: (-∞;1)U (3;+∞)
у<0:(1;3)
у=0: х= -1
у>0: (-∞;-1)U (-1;+∞)
у=0: х=-3; 1
у>0: (-3;1)
у<0:(-∞;-3)U (1;+∞)
у<0: (-∞;+∞)
Слайд 12х²-4>0 (-∞;1]
х²+3х≤0 (-∞;-2) U (2;+∞)
х²-8х+7≥0 (1;7)
х²-8х+7<0 [-3;0]
Сопоставить неравенство и его решение
![х²-4>0 (-∞;1] U [7;+∞)х²+3х≤0](/img/thumbs/f7178cacd8d268a59f14a4d522f00151-800x.jpg "Решение неравенств второй степени с одной переменной х²-4>0 (-∞;1] U [7;+∞)х²+3х≤0")
Слайд 14Проверка решения
(-∞;-3)U(3;+ ∞)
(0;2)
Нет решений
[-3;2]
(-∞;-4)U(1;+ ∞)
[1;2]
( ;4)
(-∞; ∞)
(-∞; ]U[1;+ ∞)
U(1;+ ∞)[1;2]( ;4)(-∞; ∞)(-∞; ]U[1;+ ∞)](/img/thumbs/19a59ed6ba524a8303fa2a5aa79b497f-800x.jpg "Решение неравенств второй степени с одной переменной Проверка решения(-∞;-3)U(3;+ ∞)(0;2)Нет решений[-3;2](-∞;-4)U(1;+ ∞)[1;2]( ;4)(-∞; ∞)(-∞; ]U[1;+ ∞)")
Слайд 17Список литературы
1. Ковалева С.П. Алгебра 9 класс поурочные планы.-
Волгоград: Учитель,
2. Макарычев Ю.Н. Математика 9 класс. – М.:Просвещение, 2008
3. http://festival.1september.ru/articles/504989
http://content3.files.mail.ru/
5. http://officeimg.vo.msecnd.net/en-us/images/MH900232133.jpg
6. http://officeimg.vo.msecnd.net/en-us/images/MH900343405.jpg
http://im7-tub.yandex.net/i?id=98331471-12
