- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение неравенств с одной переменной
Содержание
- 1. Решение неравенств с одной переменной
- 2. «НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ»
- 3. Решение неравенств с одной переменнойхх-31
- 4. ввести понятия «решение неравенства», «равносильные неравенства»;познакомиться со
- 5. Зная, что a < b, поставьте соответствующий
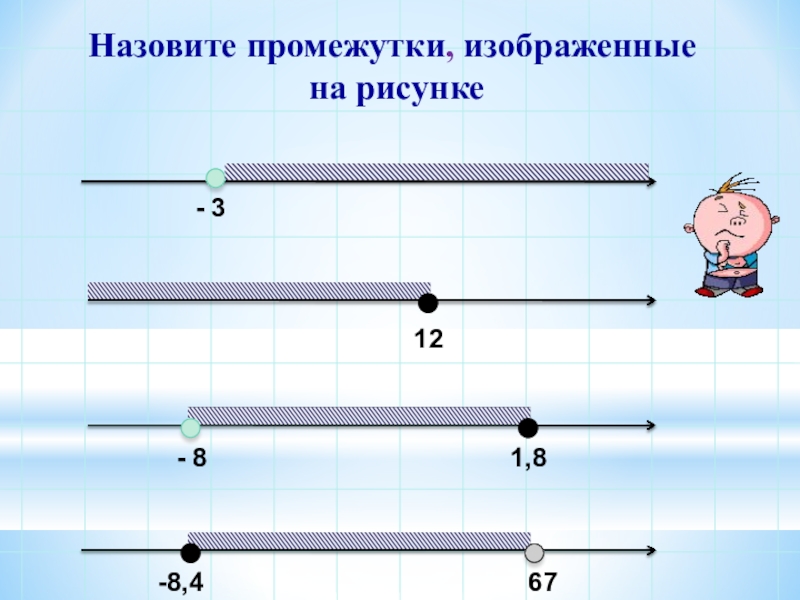
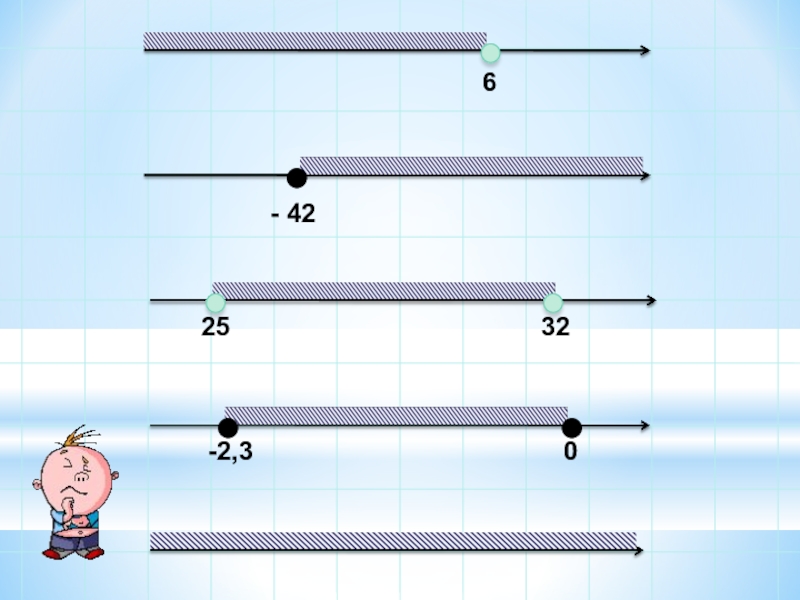
- 6. Назовите промежутки, изображенные на рисунке- 312- 8
- 7. 6- 4225
- 8. Изобразите промежутки на координатной прямой[ -2;7);
- 9. Укажите наибольшее целое число, принадлежащее промежутку: [-1;
- 10. Неравенства вида ах > b или ах
- 11. Найди ошибку!1. Х ≥7 2. y < 2,5Ответ:
- 12. Рассмотрим неравенство 5х – 14 > 3
- 13. Решением неравенства с одной переменной называется значение
- 14. Решим неравенство 4(2х – 1)
- 15. При решении неравенств используются следующие свойства:Если из
- 16. Решим неравенство
- 17. Знак изменится, когда обе
- 18. Самостоятельная работа Решите неравенство:
- 19. Работа в группах I группа (12х –
- 20. Домашнее задание●№ 844(б,в); №849(б,в)Спасибо за внимание!
Слайд 4ввести понятия «решение неравенства», «равносильные неравенства»;
познакомиться со свойствами равносильности неравенств;
рассмотреть решение
ax < b;
научиться решать неравенства с одной переменной, опираясь на свойства равносильности.
Цели урока:
Слайд 5Зная, что a < b, поставьте соответствующий знак
< или >,
1) -7а □ - 7b
2) 4а □ 4b
3) a – 3□ b – 3
4) b + 5 □ a +5
Слайд 8Изобразите промежутки на координатной прямой
[ -2;7);
(2;+∞) (-∞; +∞)
(-∞; 15]; (3;+∞)
Слайд 10Неравенства вида ах > b или ах < b, где а
Решения неравенств ах > b или ах < b при а = 0.
Пример 1. 0 • х < 24 Ответ: х – любое число
Пример2. 0 • х < - 8 Ответ: нет решений.
Линейное неравенство вида 0 • х < b или 0 • х > b, а значит и соответствующее ему исходное неравенство, либо не имеет решений, либо его решением является любое число.
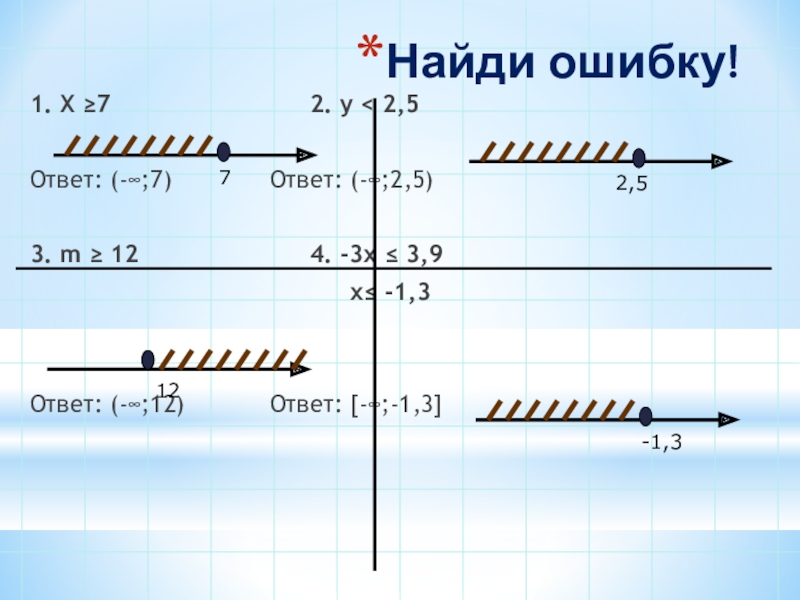
Слайд 11Найди ошибку!
1. Х ≥7 2. y < 2,5
Ответ: (-∞;7) Ответ: (-∞;2,5)
3. m ≥
x≤ -1,3
Ответ: (-∞;12) Ответ: [-∞;-1,3]
2,5
12
-1,3
Слайд 12Рассмотрим неравенство 5х – 14 > 3
при х = 6
при х = 2 5 • 2 – 14 > 3, - 4> 3 – неверно;
Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
Слайд 13Решением неравенства с одной переменной называется значение переменной, которое обращает его
Являются ли числа 3; 0,4 решением неравенства:
а) 2х – 1 < 4;
б) - 4х + 5 > 3?
Решить неравенство – значит найти все
его решения или доказать, что их нет.
Слайд 14Решим неравенство
4(2х – 1) > 3(х + 2) +
Раскроем скобки и
приведём подобные слагаемые:
Сгруппируем в левой части слагаемые с переменной, а в правой - без переменной:
Приведём подобные слагаемые:
Разделим обе части неравенства на положительное число 3, сохраняя при этом знак неравенства:
8х – 4 > 3х + 6 + х + 6
8х – 4 > 4х + 12
8х – 4х > 12 + 4
4х > 16
х > 4
4
Ответ: (4; + ∞)
Слайд 15При решении неравенств используются следующие свойства:
Если из одной части неравенства перенести
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Слайд 16Решим неравенство
Умножим обе части неравенства на наименьший общий знаменатель дробей, входящих в неравенство, т. е. на положительное число 6:
Приведём подобные слагаемые:
Разделим обе части на отрицательное число – 1, изменив знак неравенства на противоположный:
2х – 3х > 12
- х > 12
х < - 12
- 12 х
-
> 2 • 6
Слайд 17 Знак изменится, когда обе части неравенства разделить на
1) – 2х < 4
2) – 2х > 6
3) – 2х ≤ 6
Решите неравенство:
4) – х < 12
5) – х ≤ 0
6) – х ≥ 4
х > - 2
х < - 3
х ≥ - 3
х > - 12
х ≥ 0
х ≤ - 4
Слайд 18
Самостоятельная работа
Решите неравенство:
4 +12х > 7+13х;
-(2-3х)+4(6+х) >1; (4-5х)+2(3+х)< 2;
Слайд 19Работа в группах
I группа (12х – 1)(3х + 1) ≥
II группа (2х – 5)2 – 0,5х < (2х – 1)(2х + 1) – 15





![Решение неравенств с одной переменной Изобразите промежутки на координатной прямой[ -2;7); [8; 10]; Изобразите промежутки на координатной прямой[ -2;7); [8; 10];](/img/thumbs/dd621e928b3d190f245afc76a8b81f70-800x.jpg)
![Решение неравенств с одной переменной Укажите наибольшее целое число, принадлежащее промежутку: [-1; 4] (- Укажите наибольшее целое число, принадлежащее промежутку: [-1; 4] (- ∞; 3) (2;](/img/thumbs/25686cc9158060aa44422000c8d7b639-800x.jpg)