- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение неравенств с модулями
Содержание
- 1. Решение неравенств с модулями
- 2. Неравенства вида |f(x)| < a при a
- 3. Решить неравенство : |3 - 8x2| >
- 4. Решить неравенство: |x2 - 2x| ≤ 0Решением
- 5. Решить неравенство : |x2 - 7x| ≥
- 6. Решение.(6x – 8)(x – 3) ≥ 0x
- 7. Неравенства вида |f(x)|≤ g(x) сводятся к равносильной
- 8. Решить неравенство : |x2 - 8x +
- 9. Решить неравенство : |x2 – 2x -
- 10. Неравенства вида F(|f(x)|) v 0 заменой y=|f(x)|
- 11. Решить неравенство : |x - 4|3 +
- 12. Таким образом, y 3 + y –
- 13. Неравенства вида F(ϕ(x) ;|f(x)|) v 0 сводятся
- 14. Решить неравенство : x2 + 2|x +
- 15. Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения,
- 16. Решить неравенство : |2x - 5| -
- 17. Неравенства вида |f1(x)|±|f2(x)|±…±|fn(x)| v a решаются тем
- 18. Решить неравенство : |x|- 2|x + 1|+
- 19. Этот интервал входит в интервал I и
- 20. ! Презентация составлена
- 21. Слайд 21
Слайд 2Неравенства вида |f(x)| < a при a ≤ 0 решений не
Неравенства вида |f(x)| > a при a ≤ 0 имеют решением всю область определения функции f(x). При a > 0 исходное неравенство равносильно двум неравенствам : f(x) > a и f(x) < -a, при этом решения обоих неравенств являются решениями исходного. Это справедливо и для нестрогих неравенств.
Слайд 3Решить неравенство : |3 - 8x2| > -3
Решение.
Поскольку модуль всегда заведомо
Слайд 4Решить неравенство: |x2 - 2x| ≤ 0
Решением этого неравенства будут корни
Ответ : x ϵ {0} ᴜ {2}
Решить неравенство : |7x2 + 8| ≤ -3
Неравенство решений не имеет, так как модуль всегда положителен.
Решение.
Решение.
Слайд 5Решить неравенство : |x2 - 7x| ≥ 12
Решение.
Равносильные неравенства x2 -
Решаем первое неравенство.
Решаем второе неравенство.
Следовательно, решением исходного неравенства будут три интервала решений квадратных неравенств.
Слайд 7Неравенства вида |f(x)|≤ g(x) сводятся к равносильной системе:
f(x) ≤ g(x)
f(x) ≥
а неравенства вида |f(x)|≥ g(x) – к аналогичной равносильной системе:
f(x) ≥ g(x)
f(x) ≤ -g(x) .
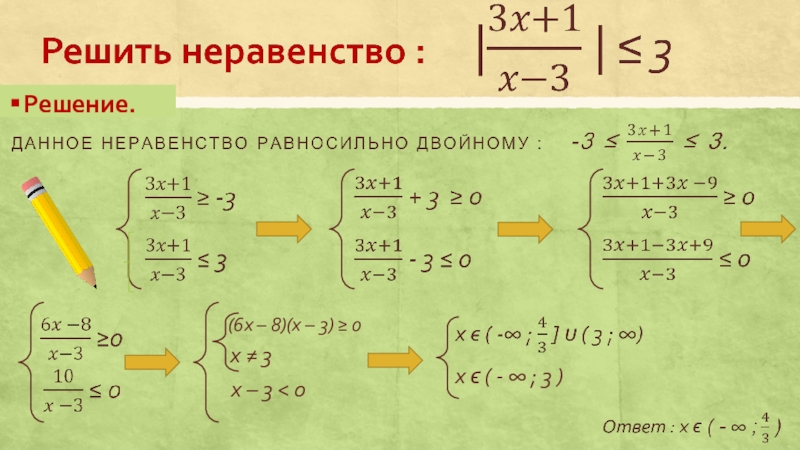
Слайд 8Решить неравенство : |x2 - 8x + 15|< x - 3
Решение
Равносильная система неравенств
x2 - 8x + 15 < x – 3
x2 - 8x + 15 > 3 - x
сводится к решению двух равносильных неравенств :
x2 - 9x + 18 < 0
x2 - 7x + 12 > 0
x1 = 3
x2 = 6
x1 = 3
x2 = 4
x ϵ ( 3 ; 6 )
x ϵ ( -∞ ; 3) ᴜ ( 4 ; ∞ )
Ответ : x ϵ ( 4 ; 6 )
3
3
4
6
Слайд 9Решить неравенство : |x2 – 2x - 3| > 3x -
Решение .
Равносильная система неравенств
x2 – 2x – 3 > 3x – 3
x2 – 2x – 3 < 3 – 3x
как и в предыдущем примере, сводится к системе квадратных неравенств :
x2 –5x > 0
x2 + x – 6 < 0
x1 = 0
x2 = 5
x1 = -3
x2 = 2
x ϵ ( -∞ ; 0 ) ᴜ ( 5 ; ∞ )
x ϵ ( -3 ; 2 )
-3
2
0
5
Ответ : x ϵ ( -3 ; 0 )
Слайд 10Неравенства вида F(|f(x)|) v 0 заменой y=|f(x)| сводятся к равносильной системе
F(y) v 0
y ≥ 0
Слайд 11Решить неравенство : |x - 4|3 + |x - 4|> 2
Решение
Заменой y=|x - 4| исходное неравенство сводится к равносильной системе :
y 3 + y > 2
y ≥ 0
y3 + y – 2
y3 – y2
y2 + y
y2 – y
2у – 2
2у – 2
y - 1
y2 + y + 2
0
-
-
-
Первое неравенство y 3 + y - 2 > 0 – рациональное. Решать его нужно методом интервалов для рациональных и дробно-рациональных неравенств, предварительно разложив левую часть на множители. Корень у=1 кубического трехчлена угадывается сразу. Поэтому, деля y 3 + y - 2 на у – 1 или применяя метод неопределенных коэффициентов с использованием теоремы Безу, разложим выражение на два сомножителя – линейный и квадратный.
Слайд 12Таким образом,
y 3 + y – 2 = (у –
Итак, равносильная система приняла вид :
(у – 1)(y2 + y + 2)>0
y≥0 ,
откуда у>1
Переходя к переменной х, получаем простейшее неравенство |х - 4| > 1, которое разбивается на два равносильных : х – 4 > 1, или х > 5, и х – 4 < -1, или х<3. Таким образом, x ϵ ( -∞ ; 3) ᴜ ( 5; ∞ ).
Ответ : x ϵ ( -∞ ; 3) ᴜ ( 5 ; ∞ )
Слайд 13Неравенства вида F(ϕ(x) ;|f(x)|) v 0 сводятся к двум равносильным системам
f(x)≥0
F(ϕ(x) ; f(x)) v 0
f(x)< 0
F(ϕ(x) ; -f(x)) v 0
Слайд 14Решить неравенство : x2 + 2|x + 3| - 10 ≤
Решение .
Равносильные системы :
x + 3 ≥ 0
x2 + 2(x + 3) – 10 ≤ 0
x + 3 < 0
x2 - 2(x + 3) – 10 ≤ 0
x ≥ -3
x2 + 2x – 4 ≤ 0
x < -3
x2 - 2x – 16 ≤ 0
и
Слайд 15Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения, сводятся к равносильному
Слайд 16Решить неравенство : |2x - 5| - |4x + 7|≥ 0
Решение .
Приводим исходное неравенство к виду
|2x - 5| ≥ |4x + 7|
и возводим в квадрат :
(2x – 5)2 ≥ (4x + 7)2
Раскрывая скобки и приводя подобные члены, получаем квадратное неравенство :
3x2 + 19x + 6 ≤ 0
3x2 + 19x + 6 = 0
Слайд 17Неравенства вида |f1(x)|±|f2(x)|±…±|fn(x)| v a решаются тем же самым методом интервалов,
Не следует путать этот метод с методом интервалов, применяемым для решения рациональных и дробно-рациональных неравенств.
Внимание!
Слайд 18Решить неравенство : |x|- 2|x + 1|+ 3|x + 2|≥ 4
Решение
Найдем сначала все xi , разбивающие числовую ось на интервалы и получающиеся как решения уравнений fj (xi )=0 : х=0; х + 1=0 ; х + 2=0. Таким образом, границами интервалов являются числа x1=0, x2=-1 и x3=-2. Отметим эти значения на числовой оси для каждого из полученных интервалов определим знаки выражений, стоящих под знаком модуля :
I
II
III
IV
-2
-1
0
x<0
x + 1 < 0
x + 2 < 0
x<0
x + 1 < 0
x + 2 > 0
x<0
x + 1 > 0
x + 2 > 0
x>0
x + 1 > 0
x + 2 > 0
Раскроем модули на интервале I (x≤-2) :
-x + 2( + 1) – 3(x + 2) ≥ 4
После преобразования получаем
-2х – 4 ≥ 4 ,
откуда х ≤ -4
Слайд 19Этот интервал входит в интервал I и является решением исходного неравенства.
II
-х+ 2(х + 1) + 3(х + 2) ≥ 4
4х + 8 ≥ 4 ,
откуда х≥-1
Решением в этом интервале является точка х=-1
III интервал ( -1≤ х ≤0 ) :
-х – 2(х + 1) + 3(х + 2) ≥ 4
4 ≥ 4
В результате мы получили истинное неравенство ( заметим, что, если бы неравенство было строгим, оно становилось бы ложным). Следовательно, весь интервал III является решением исходного неравенства.
IV интервал ( х≥0 )
х – 2(х + 1) + 3( + 2) ≥ 4
2х + 4 ≥ 4 ,
откуда х≥0
Ответ : ( -∞ ; -4 ] ᴜ [ -1 ; ∞ )
Слайд 20
! Презентация составлена
учителем математики
Абрамовой С.И.
К элективному курсу
« Решение Неравенств модулями»
24.12.18г





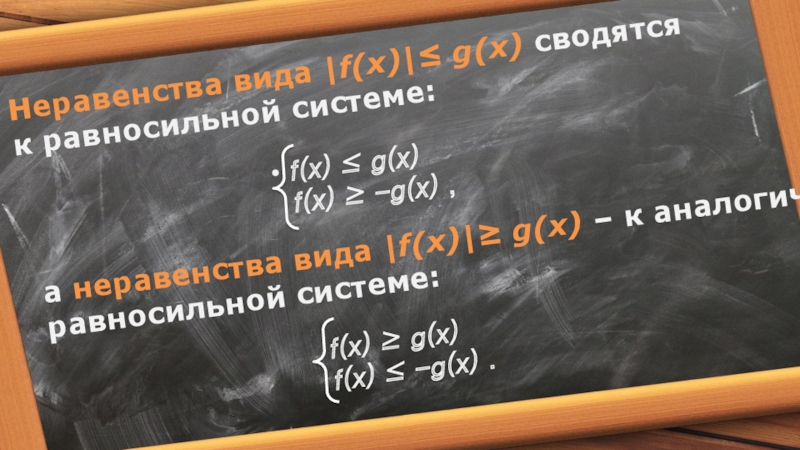







![Решение неравенств с модулями Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения, сводятся к равносильному Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения, сводятся к равносильному [ f(x) ]2 > [](/img/tmb/8/711549/a880cd1ca07df19f1ecf8d8741a96166-800x.jpg)