Методическая разработка
Учитель математики
Руденко С.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение нелинейных уравнений.Методическая разработка.
Содержание
- 1. Решение нелинейных уравнений.Методическая разработка.
- 2. *Введение Актуальность исследования. Использование новых
- 3. *ПримерА х+в= 0ax2 + bx + c
- 4. *Цель Цель исследования: 1.Изучить метод деления отрезка
- 5. *В нашей работе мы рассмотримОбласть исследования: Численные
- 6. *Алгоритм метода Известно, что любой
- 7. * Переносится та граница, со стороны которой
- 8. *
- 9. * Пусть дано уравнение f(x)=0, функция
- 10. *
- 11. *Блок-схема метода
- 12. *Программа:Program XXX; Uses Crt; Var a, b,
- 13. *
- 14. *Рассмотрим задачу1 марта 1996г. некоторая фирма по
- 15. *Решение задачи. Обозначим искомую стоимость набора товаров
- 16. *
- 17. *Рассмотрим данную задачу в условиях современного
- 18. *Обозначим искомую стоимость набора товаров и услуг
- 19. *
- 20. * Практическое применение .Эта программа поможет вам
- 21. *1.Установи диск.2.Открой папку .3.Левой кнопкой мыши щелкни 2 раза по пиктограмме, открой программу.4.Появиться окно программы:
- 22. *5. Выполни команду: File- Open.6.Появиться окно:
- 23. *7.Выбери файл :Otrezok8- ok.
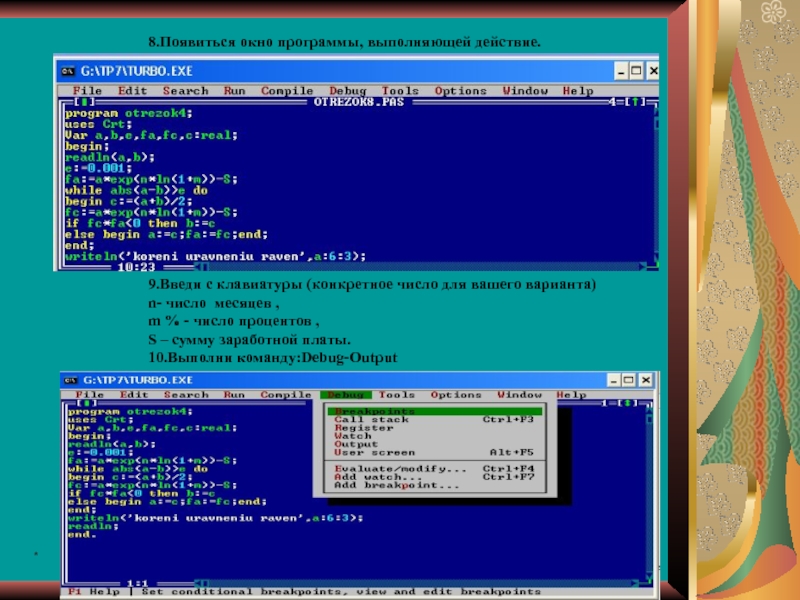
- 24. *8.Появиться окно программы, выполняющей действие.9.Введи с клавиатуры
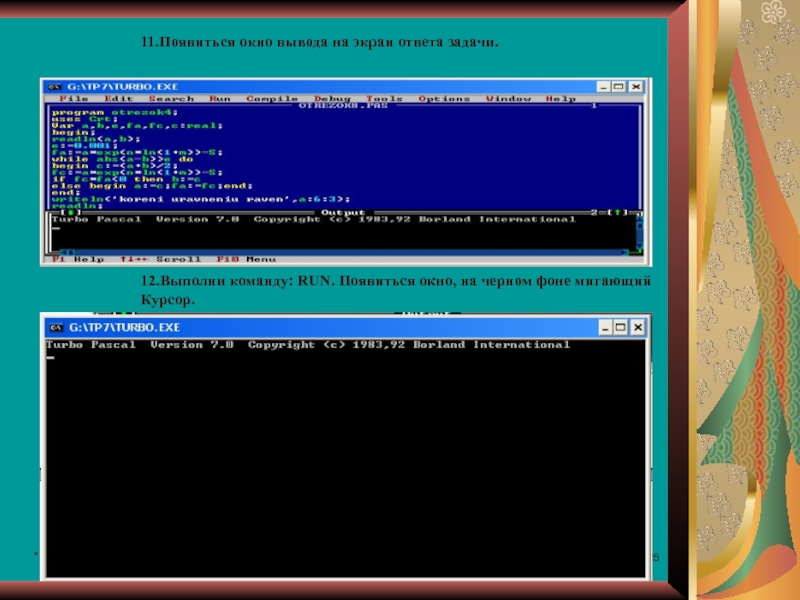
- 25. *11.Появиться окно вывода на экран ответа задачи.12.Выполни команду: RUN. Появиться окно, на черном фоне мигающий Курсор.
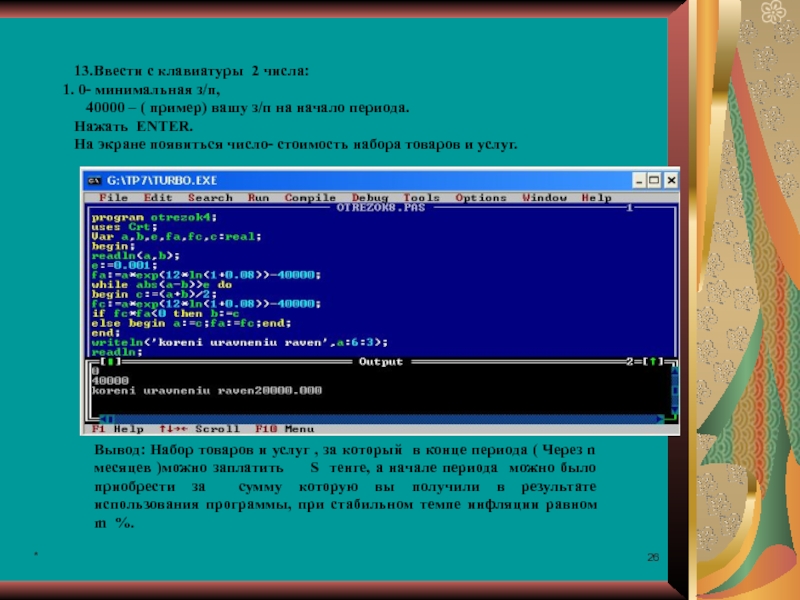
- 26. *13.Ввести с клавиатуры 2 числа: 0- минимальная
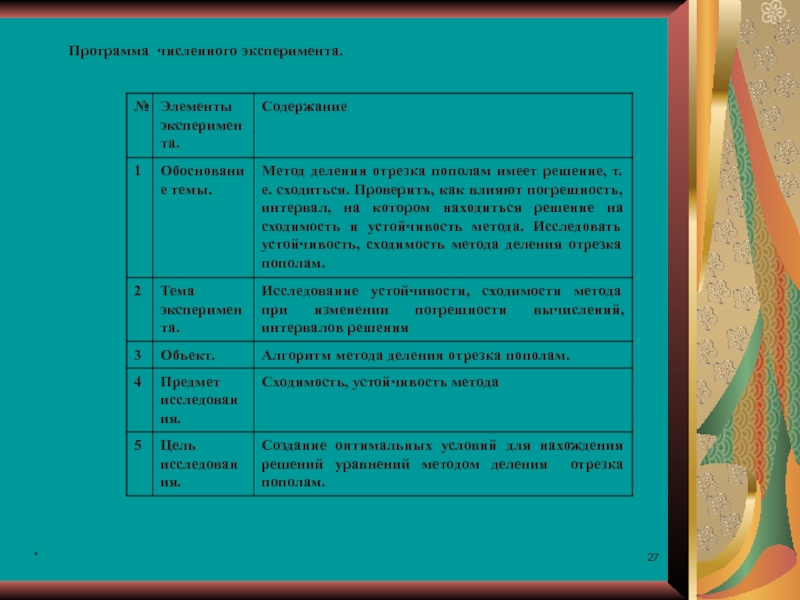
- 27. * Программа численного эксперимента.
- 28. *
- 29. *
- 30. *Результаты проведенных исследований.Численный эксперимент. е =0,001Интервал (0,25).Интервал:(0,20).
- 31. *Итоги эксперимента представим в виде таблицы:
- 32. *Итоги экспериментаАнализируя представленную таблицу нужно определить, что:Устойчивость
- 33. *Итоги экспериментаАнализируя представленную таблицу можно сделать выводы:1.
- 34. *
- 35. * - и +
Слайд 1*
Школа-гимназия № 1 им.А.С.Пушкина
г.Чимкент
Решение нелинейных уравнений методом деления отрезка пополам
Слайд 2*
Введение
Актуальность исследования. Использование новых информационных технологий позволяет
Слайд 4*
Цель
Цель исследования:
1.Изучить метод деления отрезка пополам.
2.Составить программу для реализации
3.Решить с помощью метода прикладные задачи.
4. Исследовать сходимость и устойчивость метода, провести численный эксперимент
Слайд 5*
В нашей работе мы рассмотрим
Область исследования: Численные методы решения уравнений.
Предмет исследования:
Гипотеза исследования:
Если для решения нелинейных уравнений и получения более точных приближенных решений использовать метод деления отрезка пополам , то следует уменьшить ε погрешность вычислений , уменьшить интервал поиска решений.
Слайд 6*
Алгоритм метода
Известно, что любой метод является
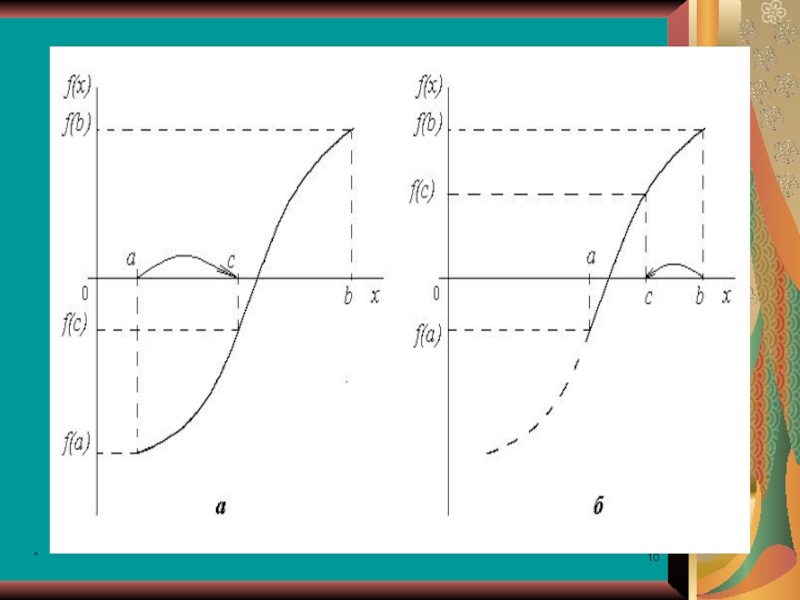
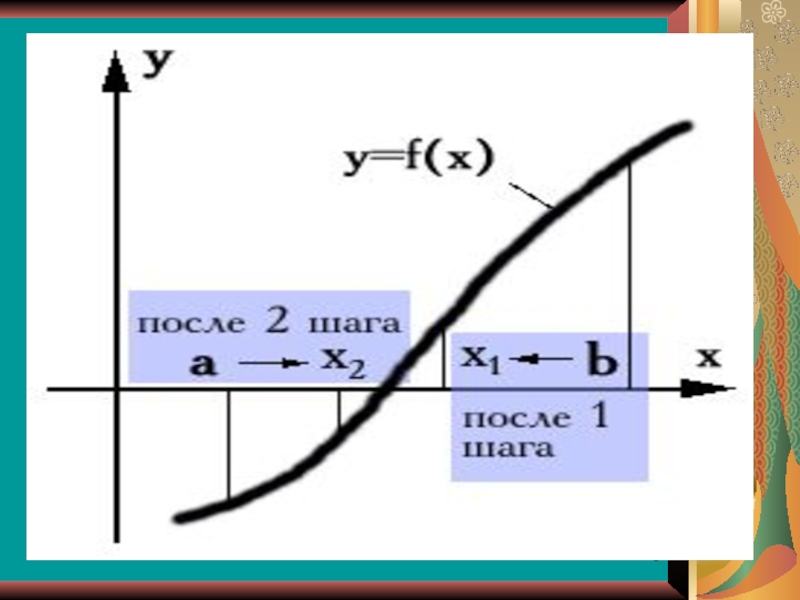
Метод половинного деления или дихотомии (дихотомия - сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину..
Слайд 7*
Переносится та граница, со стороны которой функция на половине отрезка
Слайд 9*
Пусть дано уравнение f(x)=0,
функция f(x) непрерывна на интервале [a,b].
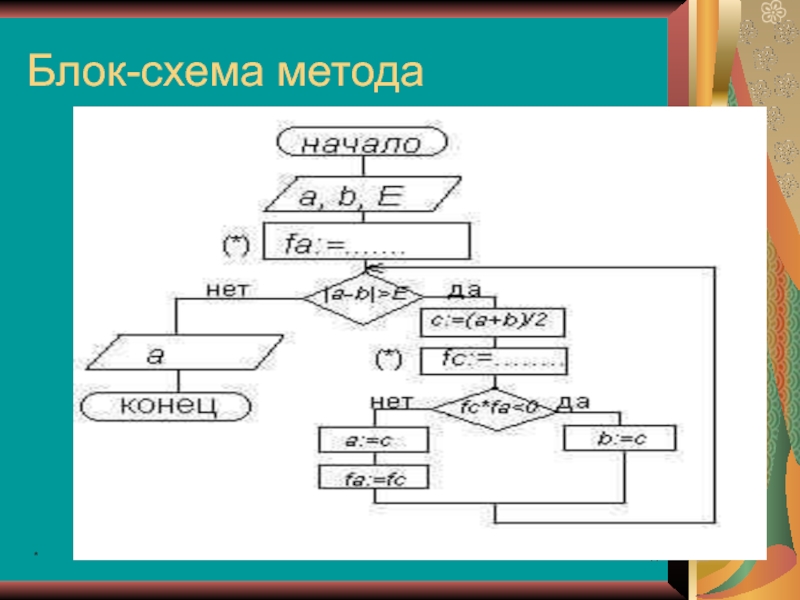
При такой постановке алгоритм метода деления отрезка пополам следующий:
1) c = (a + b)/2 {вычисляем середину
отрезка [a, b]}, f(C) .
2) если f(a) * f(C) < 0, то b = c , иначе a = c. {выбираем левую или правую часть отрезка, где находится корень уравнения}
3) если |a – b| > E, то перейти к пункту 1). {если величина длины отрезка не достигла требуемой точности, то процесс деления отрезка продолжаем}
Любая точка отрезка [a, b] при таком алгоритме даст приближенное решение с заданной точностью.
Слайд 12*
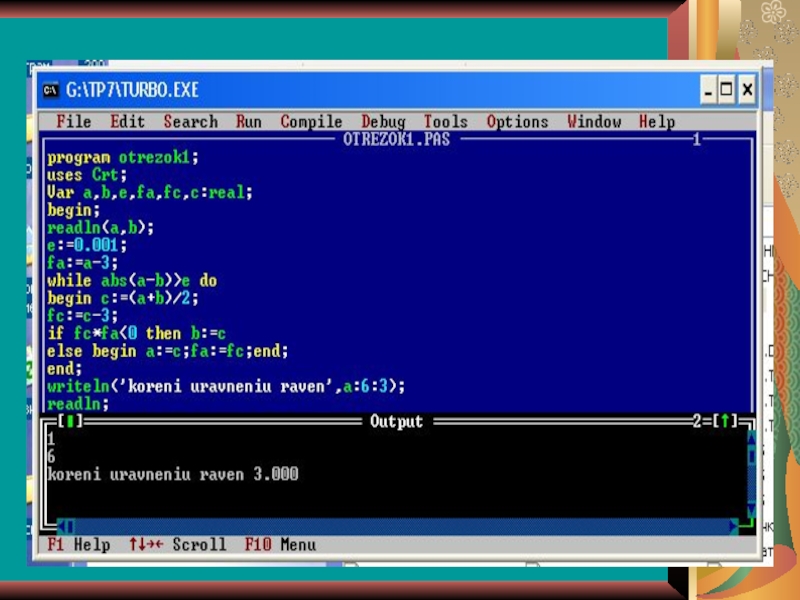
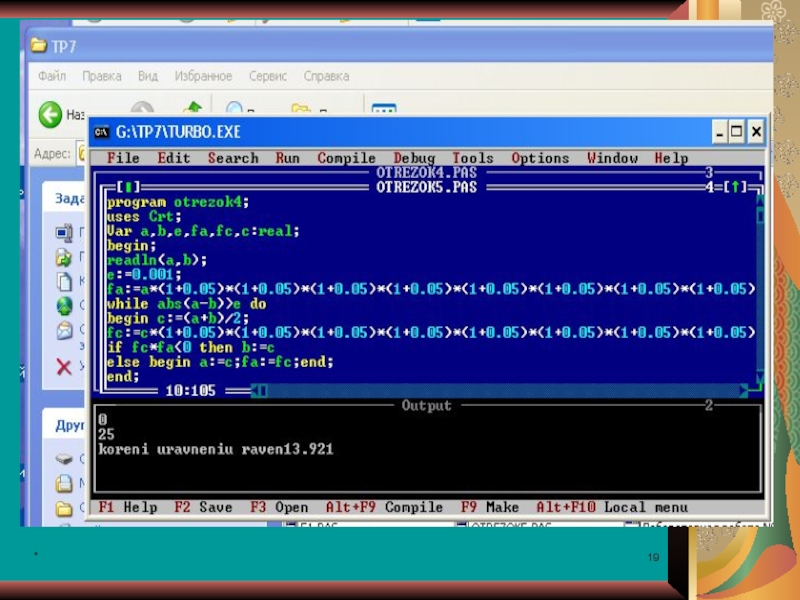
Программа:
Program XXX;
Uses Crt;
Var a, b, e, fa, fc, c: Real;
Begin ;
e : = 0.001; fa : = … ; While Abs (a – b) > e do Begin c : = (a + b)/2; fc : = … ; If fc . fa < 0 Then
b : = c Else
Begin a : = c; fa : = fc; end; end; Writeln (‘Корень уравнения равен ’, a : 6 : 3);
End.
Слайд 14*
Рассмотрим задачу
1 марта 1996г. некоторая фирма по добыче газа добилась погашения
Определите ,сколько стоил на 1 декабря 1995 г. тот набор товаров и услуг, который можно приобрести на 1 марта 1996г. на полученные 400 тыс. тенге, если темп инфляции был стабилен и равнялся 8% в месяц.
Слайд 15*
Решение задачи.
Обозначим
искомую стоимость набора товаров и услуг как –
При стабильном месячном темпе инфляции стоимость этого набора через
n месяцев составит:
Уn = У * ( 1 + 0,08)n . (1)
По условию задачи n = 3 (месяца), Уn = 400 (тыс. тенге) ,
Таким образом :
У * ( 1 + 0,08)3 = 400,
Слайд 17*
Рассмотрим данную задачу в условиях современного состояния экономики.
Известно, темп инфляции
1 января 2008 г. средняя зарплата в Казахстане 25 000 тенге. При условии сохранения заработной платы, до конца года, определим сколько стоил на 1 января 2008 г. тот набор товаров и услуг, который можно приобрести на 31 декабря 2008г. на полученные 25 000 тыс.тенге, если темп инфляции был стабилен и равнялся 5% в месяц.
Слайд 18*
Обозначим искомую стоимость набора товаров и услуг как – У (тыс.
При стабильном месячном темпе инфляции стоимость этого набора через
n месяцев составит:
Уn = У * ( 1 + 0,05)n . (1)
По условию задачи n = 12 (месяца), Уn = 25 (тыс. тенге) ,
Таким образом :
У * ( 1 + 0,05)12 = 25, (2)
Слайд 20*
Практическое применение .
Эта программа поможет вам подсчитать стоимость набора товаров
n- месяцев,
с учетом m процента инфляции ,
если твоя зарплата составляет S тенге.
Выполни следующие действия:
Слайд 21*
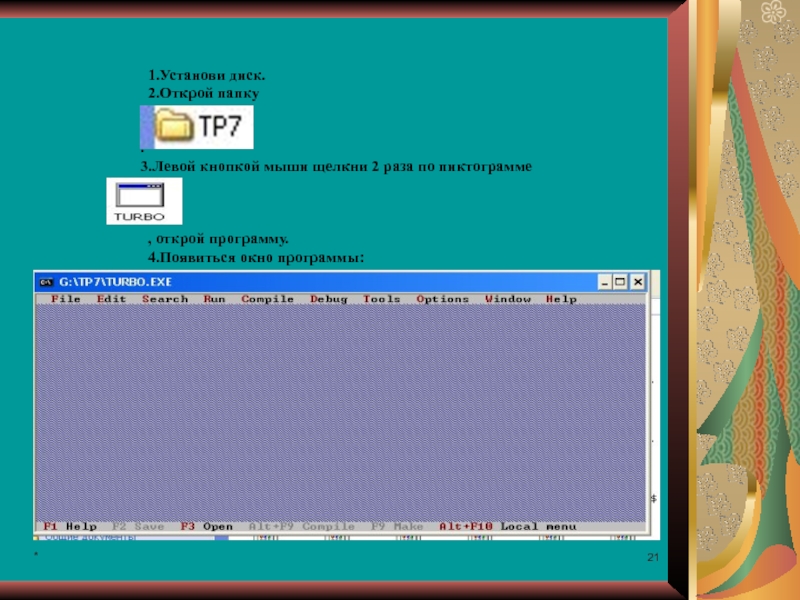
1.Установи диск.
2.Открой папку
.
3.Левой кнопкой мыши щелкни 2 раза по пиктограмме
,
4.Появиться окно программы:
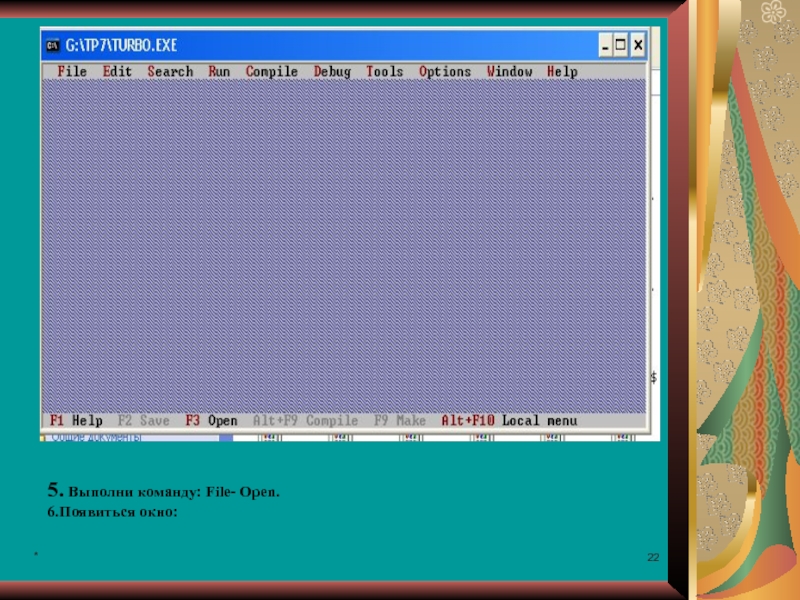
Слайд 24*
8.Появиться окно программы, выполняющей действие.
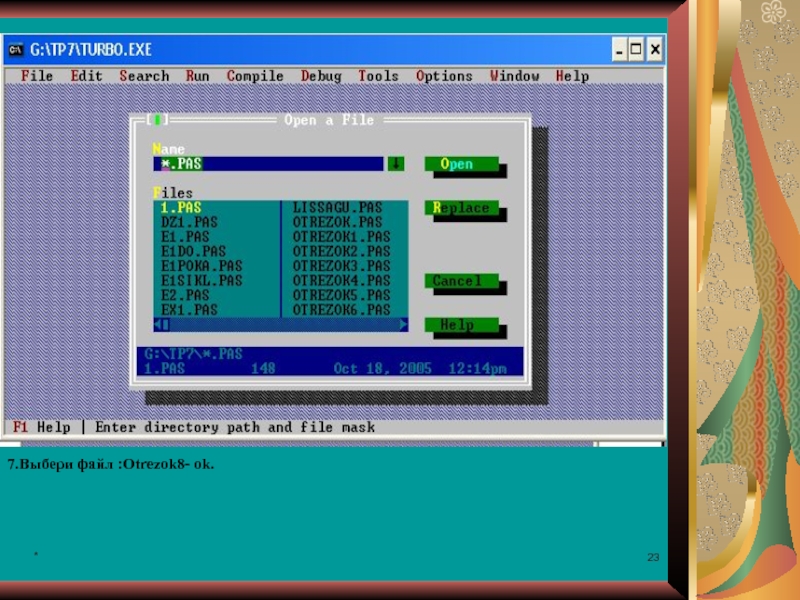
9.Введи с клавиатуры (конкретное число для вашего
n- число месяцев ,
m % - число процентов ,
S – сумму заработной платы.
10.Выполни команду:Debug-Output
Слайд 25*
11.Появиться окно вывода на экран ответа задачи.
12.Выполни команду: RUN. Появиться окно,
Курсор.
Слайд 26*
13.Ввести с клавиатуры 2 числа:
0- минимальная з/п,
40000 –
Нажать ENTER.
На экране появиться число- стоимость набора товаров и услуг.
Вывод: Набор товаров и услуг , за который в конце периода ( Через n месяцев )можно заплатить S тенге, а начале периода можно было приобрести за сумму которую вы получили в результате использования программы, при стабильном темпе инфляции равном m %.
Слайд 30*
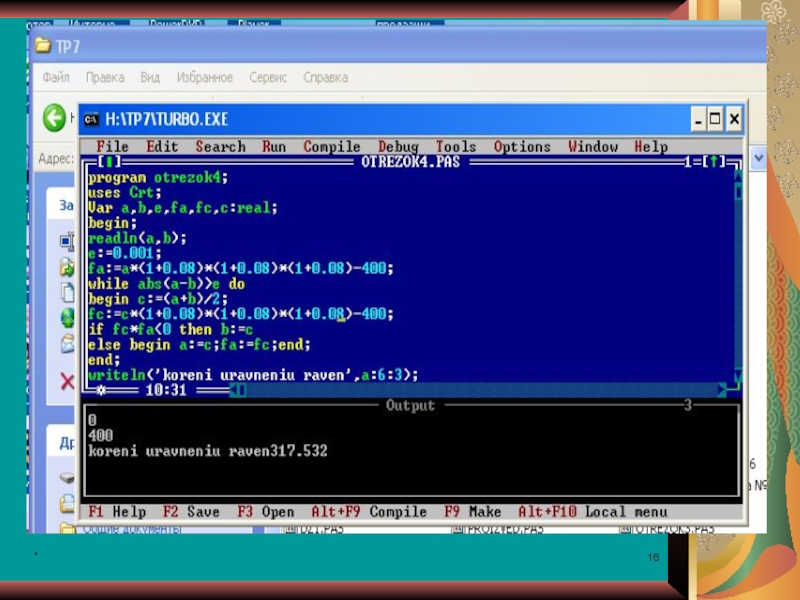
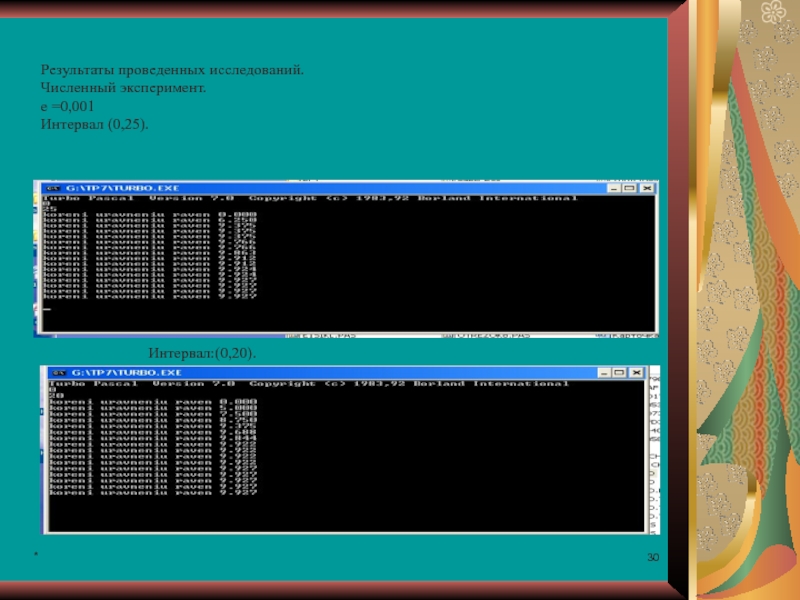
Результаты проведенных исследований.
Численный эксперимент.
е =0,001
Интервал (0,25).
Интервал:(0,20).
Слайд 32*
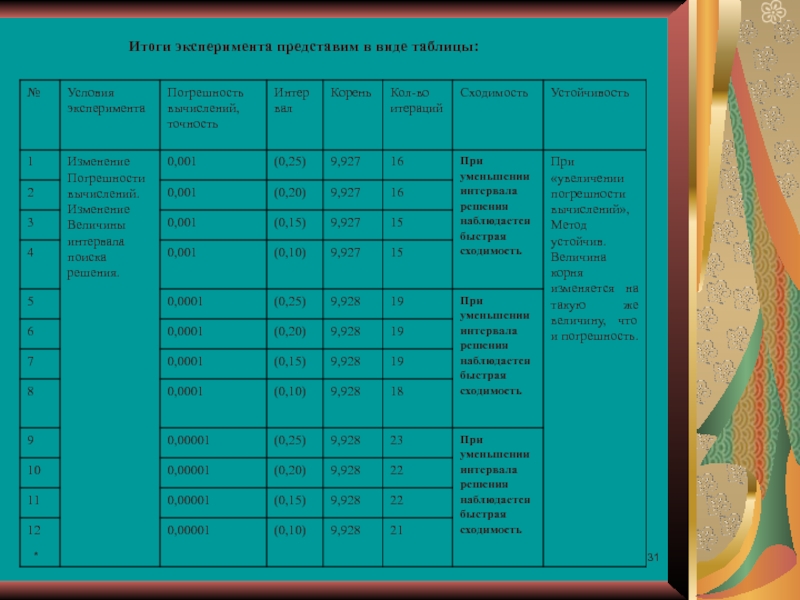
Итоги эксперимента
Анализируя представленную таблицу нужно определить, что:
Устойчивость численного метода- зависимость выходных
Сходимость алгоритма – наличие решения, и как быстро находиться это решение.
Если в результате исполнения алгоритма решение находиться быстро, то говорят, что имеется «Быстрая сходимость», в противном случае – наоборот.
Слайд 33*
Итоги эксперимента
Анализируя представленную таблицу можно сделать выводы:
1. При изменении погрешности
Другими словами: для более точного нахождения решения методом деления отрезка пополам нужно больше программного времени.
2. При уменьшении интервала поиска решения наблюдается «более быстрая сходимость».
Метод устойчив. Изменение интервалов решения не влияет на решение, если решение находится в данном интервале.
Слайд 34*
Заключение:
Цели достигнуты.
В работе мы
научились находить решения уравнений методом деления отрезка пополам,
использовать язык программирования Паскаль для реализации циклических алгоритмов.
Новизна работы состоит в применении метода для решения экономических задач.
Слайд 35*
- и + данного метода
Достоинством
интервале [a, b] имеется хотя бы один корень.
Кроме того, метод не использует производных.
Простота;
Быстрое достижение результата.
К недостаткам относят медленную сходимость,
т.е. достаточно большое число вычислений функции f(x) по сравнению с другими методами.
Рекомендуется к использованию в тех случаях, если нет жестких требований ко времени счета.
Необходимо заранее знать отрезок, на котором функция меняет знак, что не совсем удобно.







![Решение нелинейных уравнений.Методическая разработка. * Пусть дано уравнение f(x)=0, функция f(x) непрерывна на интервале [a,b]. * Пусть дано уравнение f(x)=0, функция f(x) непрерывна на интервале [a,b]. Условие f(a)× f(b) E,](/img/thumbs/a7b39e271e2f309f4c5bf47dbc1a8e02-800x.jpg)