О.М.
МО, г.о. Воскресенск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение логических уравнений в школьном курсе математики с помощью метода мажорант
Содержание
- 1. Решение логических уравнений в школьном курсе математики с помощью метода мажорант
- 2. ВведениеМетод мажорант применяется при решении нестандартных уравнений и
- 3. Пусть у нас имеется уравнение f(x) =
- 4. «Внешний вид» задач, где явно напрашивается метод
- 5. Основная частьРешим уравнение:Рассмотрим левую часть:Свойство тригонометрических ф.АналогичноПомножим на -1
- 6. Прибавим 17 ко всем трем частямБерем логарифм
- 7. Рассмотрим правую частьРассмотрим подкоренное выражение, выделим полный
- 8. Состыкуем результаты наших оценокТеперь уже видно, что
- 9. Таким образом, образуется системаВторое уравнение решим, возведя
- 10. Рассмотрим задание 13 из ЕГЭ.a) Решите уравнение: б) Найдите все корни уравнения, на промежутке
- 11. 1. Оценим, в каких пределах может
- 12. 2. Оценим, в каких пределах может принимать значения правая часть неравенства:Таким образом, можно составить систему:
- 13. Найдем при каких значениях выполняется равенство
- 14. Итак, левая часть уравнения равна 1 приНайдем при каких значениях х правая часть равна 1.
- 15. Итак, правая часть уравнения равна 1 при:Система примет вид:
- 16. Выпишем значения х из промежутка [0;2П].
- 17. Мы видим, что при
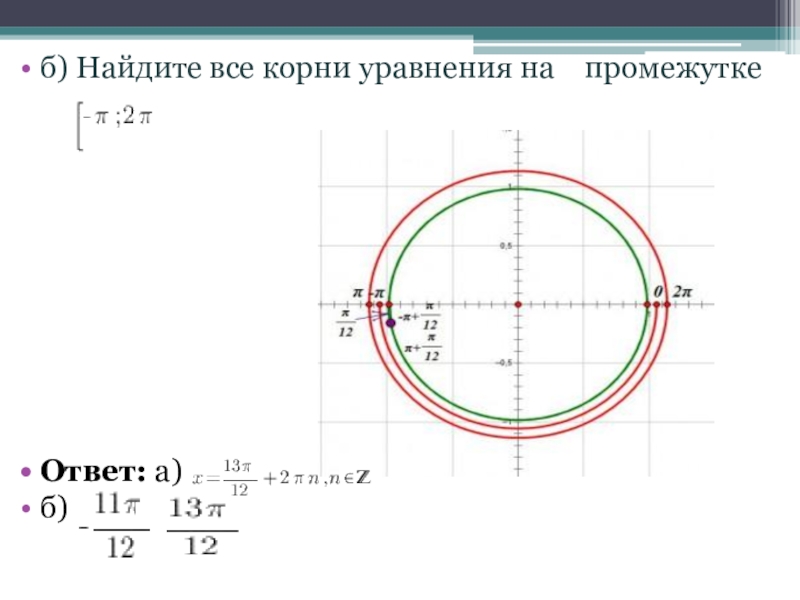
- 18. б) Найдите все корни уравнения на промежуткеОтвет: а) б)
- 19. ЗаключениеМногие функции, которые нам известны, имеют мажоранты.
ВведениеМетод мажорант применяется при решении нестандартных уравнений и неравенств, которые не получается решить с помощью стандартных приемов. Название метода мажорант происходит от французских слов majorer - объявлять большим и minorer - объявлять меньшим.При подготовке к ЕГЭ по математике, если вы хотите научиться
Слайд 1Решение логарифмических уравнений в школьном курсе с помощью метода мажорант
учитель математики
Байдакова
Слайд 2Введение
Метод мажорант применяется при решении нестандартных уравнений и неравенств, которые не получается
решить с помощью стандартных приемов.
Название метода мажорант происходит от французских слов majorer - объявлять большим и minorer - объявлять меньшим.
При подготовке к ЕГЭ по математике, если вы хотите научиться решать задания группы С, с этим методом необходимо познакомиться.
Название метода мажорант происходит от французских слов majorer - объявлять большим и minorer - объявлять меньшим.
При подготовке к ЕГЭ по математике, если вы хотите научиться решать задания группы С, с этим методом необходимо познакомиться.
Слайд 3Пусть у нас имеется уравнение f(x) = g(x). Допустим, мы каким-то
образом установили, что левая часть не больше какого-то числа А:
Также мы установили, что правая часть не меньше этого же числа:
f(x) = g(x) равносильно системе:
Также мы установили, что правая часть не меньше этого же числа:
f(x) = g(x) равносильно системе:
Слайд 4«Внешний вид» задач, где явно напрашивается метод оценок, примерно следующий:
-наличие слева
и справа «разнородных» функций (синуса и логарифма, косинуса и квадратного трёхчлена и т.п.);
-присутствие ограниченных конструкций (синусов/косинусов, квадратных трёхчленов, модулей, суммы взаимно обратных величин и т.д.).
-присутствие ограниченных конструкций (синусов/косинусов, квадратных трёхчленов, модулей, суммы взаимно обратных величин и т.д.).
Слайд 5Основная часть
Решим уравнение:
Рассмотрим левую часть:
Свойство тригонометрических ф.
Аналогично
Помножим на -1
Слайд 6Прибавим 17 ко всем трем частям
Берем логарифм по основанию 2
Значит, вся
конструкция слева заключена в отрезке [4; log217]. Иначе быть не может.
Слайд 7Рассмотрим правую часть
Рассмотрим подкоренное выражение, выделим полный квадрат
Отсюда следует:
Значит, если
из этого выражения извлечь корень, то он точно будет не больше , т.е. 4. Итак,
Слайд 8Состыкуем результаты наших оценок
Теперь уже видно, что нашим разделяющим числом (т.е.
мажорантой) является четвёрка
Чтобы наше уравнение имело корни, левая и правая части одновременно должны быть равны 4.
Чтобы наше уравнение имело корни, левая и правая части одновременно должны быть равны 4.
Слайд 9Таким образом, образуется система
Второе уравнение решим, возведя обе части в квадрат,
получим x = 1
Проверим первое уравнение при x = 1:
Ответ: 1.
Проверим первое уравнение при x = 1:
Ответ: 1.
Слайд 10Рассмотрим задание 13 из ЕГЭ.
a) Решите уравнение:
б) Найдите все корни уравнения, на
промежутке
Слайд 111. Оценим, в каких пределах может принимать значения левая часть
неравенства:
Так как все части неравенства положительны, прологарифмируем неравенство:
Слайд 122. Оценим, в каких пределах может принимать значения правая часть неравенства:
Таким образом,
можно составить систему:
Слайд 17Мы видим, что при
обе части уравнения равны 1.
Итак, решение уравнения
Ответим на вторую часть задания:
Итак, решение уравнения
Ответим на вторую часть задания:
Слайд 19Заключение
Многие функции, которые нам известны, имеют мажоранты.
Если же мажоранта не
видна сразу, её можно найти, исследуя функцию.
Чтобы найти мажоранту, нужно найти наименьшее или наибольшее значение функции на промежутке.
Умение оценивать левую и правую части уравнений (неравенств) помогает успешно решать нестандартные задачи и задания повышенной сложности.
Чтобы найти мажоранту, нужно найти наименьшее или наибольшее значение функции на промежутке.
Умение оценивать левую и правую части уравнений (неравенств) помогает успешно решать нестандартные задачи и задания повышенной сложности.















![Решение логических уравнений в школьном курсе математики с помощью метода мажорант Выпишем значения х из промежутка [0;2П]. Выпишем значения х из промежутка [0;2П].](/img/thumbs/3f8ed26e1c5ab81131d342b42db0d383-800x.jpg)