- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Рациональные и иррациональные числа
Содержание
- 1. Рациональные и иррациональные числа
- 2. ПланМножествоНатуральные числаЦелые числаРациональные числаРациональные числа в виде
- 3. Множество Понятие “множество” принадлежит к одному из
- 4. Что такое число и натуральные числа Математика
- 5. Целые числаПри сложении и умножении натуральных чисел
- 6. Что такое целые числаТермин “целое число”
- 7. Рациональные числаПри сложении, умножении, вычитании целых чисел
- 8. Рациональные числа в виде дробиЧисло, которое можно
- 9. Рациональные числа. Преоразование обыкновенной дроби в десятичнуюДля
- 10. Рациональные числа. Переобразование обыкновенной дроби в десятичную.Каждую
- 11. Иррациональные числаУже пифагорийцы знали, что квадрат гипотенузы
- 12. Действительные числаМножество всех рациональных и иррациональных чисел
- 13. Выберите правильные утверджениямм
- 14. Сравните
- 15. Вычислите
- 16. Сравните>>>
ПланМножествоНатуральные числаЦелые числаРациональные числаРациональные числа в виде дробиПреобразование обыкновенной дроби в десятичнуюИррациональные числаДействительные числаВыберите правильные утвердженияСравнитеВычислитеСравните
Слайд 2План
Множество
Натуральные числа
Целые числа
Рациональные числа
Рациональные числа в виде дроби
Преобразование обыкновенной дроби в
десятичную
Иррациональные числа
Действительные числа
Выберите правильные утверджения
Сравните
Вычислите
Сравните
Иррациональные числа
Действительные числа
Выберите правильные утверджения
Сравните
Вычислите
Сравните
Слайд 3Множество
Понятие “множество” принадлежит к одному из первичных понятий математики. Множество
можно представить как савокупность некоторых предметов, объединенных по некоторым свойствам.
Пример : множество учеников отдельного класса, множество букв алфавита, множество точек на прямой.
Предметы, из которых состоит множество, называются ее элементами.
Пример: Петя из 5-А класса; электрочайник - элемент множества кухонной техники.
Пример : множество учеников отдельного класса, множество букв алфавита, множество точек на прямой.
Предметы, из которых состоит множество, называются ее элементами.
Пример: Петя из 5-А класса; электрочайник - элемент множества кухонной техники.
Слайд 4Что такое число и натуральные числа
Математика изучает количественные отношенния и
пространственные формы реального мира, для которых основным измерением является число. Понятие “число” появилось тогда, когда люди отделили его от реальных объектов и их особенностей.
Натуральные числа– числа, которые используют при счете предметов. Натуральных чисел бесконечное количество. Их записывають с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Значит, с помощью десяти цифр можно записать числа, которые используют при счете предметов , в некоторую савокупность. Такие числа образуют множество натуральных чисел. А сами числа называють ее элементами.
Термин “натуральное число” происходит от латинского слова NATURA – природа. Обозначают это множество – N.
N={ 1, 2, 3 …} – это бесконечное множество.
То, что число принадлежит или не принадлежит множеству натуральных чисел, записывают так:-15 N, 10 € N
N
1 2 3 4
Натуральные числа– числа, которые используют при счете предметов. Натуральных чисел бесконечное количество. Их записывають с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Значит, с помощью десяти цифр можно записать числа, которые используют при счете предметов , в некоторую савокупность. Такие числа образуют множество натуральных чисел. А сами числа называють ее элементами.
Термин “натуральное число” происходит от латинского слова NATURA – природа. Обозначают это множество – N.
N={ 1, 2, 3 …} – это бесконечное множество.
То, что число принадлежит или не принадлежит множеству натуральных чисел, записывают так:-15 N, 10 € N
N
1 2 3 4
Слайд 5Целые числа
При сложении и умножении натуральных чисел всегда получают натуральное число.
При этом при их вычитании не всегда получают натуральное число.
Пример: 13-15=-2, 10-10=0; числа -2 и 0 не натуральные.
Чтобы всегда выполнялось действие вычитание, ввели отрицательные числа и 0.
Множество натуральных чисел расширили до множества целых чисел.
+1, +2, +3…
-1, -2, -3, 0…
Пример: 13-15=-2, 10-10=0; числа -2 и 0 не натуральные.
Чтобы всегда выполнялось действие вычитание, ввели отрицательные числа и 0.
Множество натуральных чисел расширили до множества целых чисел.
+1, +2, +3…
-1, -2, -3, 0…
Слайд 6Что такое целые числа
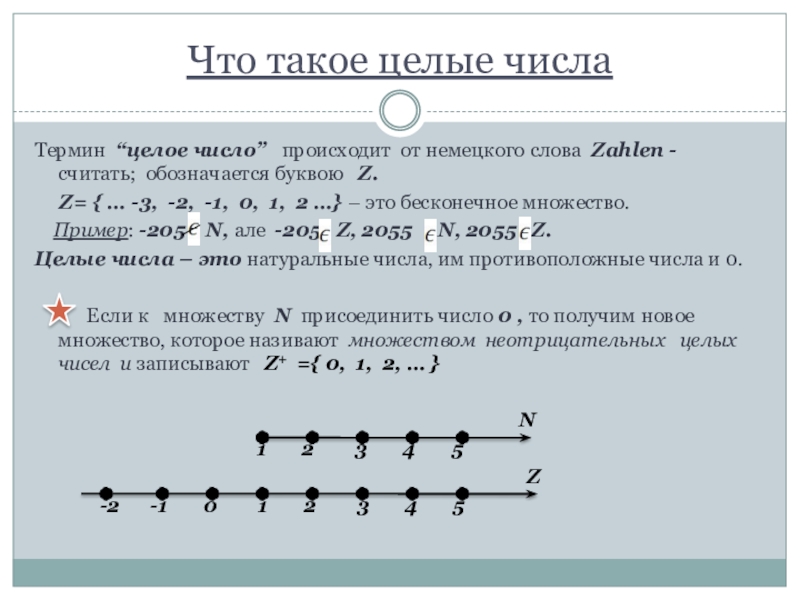
Термин “целое число” происходит от немецкого слова
Zahlen - считать; обозначается буквою Z.
Z= { … -3, -2, -1, 0, 1, 2 …} – это бесконечное множество.
Пример: -205 N, але -205 Z, 2055 N, 2055 Z.
Целые числа – это натуральные числа, им противоположные числа и 0.
Если к множеству N присоединить число 0 , то получим новое множество, которое називают множеством неотрицательных целых чисел и записывают Z+ ={ 0, 1, 2, … }
N
1 2 3 4 5
Z
-2 -1 0 1 2 3 4 5
Z= { … -3, -2, -1, 0, 1, 2 …} – это бесконечное множество.
Пример: -205 N, але -205 Z, 2055 N, 2055 Z.
Целые числа – это натуральные числа, им противоположные числа и 0.
Если к множеству N присоединить число 0 , то получим новое множество, которое називают множеством неотрицательных целых чисел и записывают Z+ ={ 0, 1, 2, … }
N
1 2 3 4 5
Z
-2 -1 0 1 2 3 4 5
Слайд 7Рациональные числа
При сложении, умножении, вычитании целых чисел всегда получают целое число.
Однако при делении двух целых чисел не всегда получают целое число.
Пример: 20:6=3 (ост. 2), то есть деление чисел 20 і 6 невозможно выполнить в множестве целых чисел.
Если расширить множество целых чисел, дополнив его дробными, то в этом расширенном множестве будут выполняться четыре арифметических действия.
Мы пришли к такому числовому множеству, в котором содержатся все целые и дробные (положительные и отрицательные) числа. Его называють множеством рациональных чисел.
Термин “рациональное число” происходит от
латинского слова Ratio – отношение (частное).
Множество рациональных чисел обозначают– Q.
Пример: 20:6=3 (ост. 2), то есть деление чисел 20 і 6 невозможно выполнить в множестве целых чисел.
Если расширить множество целых чисел, дополнив его дробными, то в этом расширенном множестве будут выполняться четыре арифметических действия.
Мы пришли к такому числовому множеству, в котором содержатся все целые и дробные (положительные и отрицательные) числа. Его называють множеством рациональных чисел.
Термин “рациональное число” происходит от
латинского слова Ratio – отношение (частное).
Множество рациональных чисел обозначают– Q.
Слайд 8Рациональные числа в виде дроби
Число, которое можно представить в виде
дроби , где m – целое число, n – натуральное, называется рациональным числом .
Любое рациональное число можно разными способами представить в виде дроби.
Пример: ; ;
Среди равных дробей всегда можно найти дробь, знаменатель которой наименший. Такая дробь называется несокротимой.
Примером множества рациональных чисел будет
множество : А={ 20; -5,2; -1; 0; 3; 8,4…}
Некоторые элементы этого множества принадлежат только множеству рациональных чисел, однако есть и такие, которые приналежат множеству целых и натуральних чисел.
-1 Q; -1 N; -1 Z; 20 Q; 20 Z; 20 N.
Любое рациональное число можно разными способами представить в виде дроби.
Пример: ; ;
Среди равных дробей всегда можно найти дробь, знаменатель которой наименший. Такая дробь называется несокротимой.
Примером множества рациональных чисел будет
множество : А={ 20; -5,2; -1; 0; 3; 8,4…}
Некоторые элементы этого множества принадлежат только множеству рациональных чисел, однако есть и такие, которые приналежат множеству целых и натуральних чисел.
-1 Q; -1 N; -1 Z; 20 Q; 20 Z; 20 N.
Слайд 9Рациональные числа. Преоразование обыкновенной дроби в десятичную
Для преоразование обыкновенной
дроби в десятичную, используют действие деление m:n. Таким образом,
При этом бывают случаи, когда деление 1) заканчивается через несколько шагов; 2) повторяются через несколько шагов; 3) преоразовывается в бесконечное повторение одной и то же самой савокупности цифр. То, что при делении повторяется один и тот же остаток и одни и те же числа в частном, называють периодичностью дроби, а савокупность цифр, что повторяется, называють периодом дроби. В записи периодичних десятичных дробей период пишут один раз, взявши его в круглые скобки.
Запись читают так:
0 целых 3 в периоде; мінус 0 целых 81 в периоде; 0 цілих 58 сотих и 3 у периоде.
При этом бывают случаи, когда деление 1) заканчивается через несколько шагов; 2) повторяются через несколько шагов; 3) преоразовывается в бесконечное повторение одной и то же самой савокупности цифр. То, что при делении повторяется один и тот же остаток и одни и те же числа в частном, называють периодичностью дроби, а савокупность цифр, что повторяется, называють периодом дроби. В записи периодичних десятичных дробей период пишут один раз, взявши его в круглые скобки.
Запись читают так:
0 целых 3 в периоде; мінус 0 целых 81 в периоде; 0 цілих 58 сотих и 3 у периоде.
Слайд 10Рациональные числа. Переобразование обыкновенной дроби в десятичную.
Каждую дробь
, де m Z , n N , можно представить в виде конечной десятичной дроби или в виде бесконечной периодической десятичной дроби.
Кождую конечную десятичную дробь можно записать в виде бесконечной дроби, приписывая справа бесконечное количество нулей. 2,7=2,7000…=2,7(0).
N
1 2 3 4 5
Z
-2 -1 0 1 2 3 4 5
Q
-2,5 -2 -1 0 1 2 3 4 5
Кождую конечную десятичную дробь можно записать в виде бесконечной дроби, приписывая справа бесконечное количество нулей. 2,7=2,7000…=2,7(0).
N
1 2 3 4 5
Z
-2 -1 0 1 2 3 4 5
Q
-2,5 -2 -1 0 1 2 3 4 5
Слайд 11Иррациональные числа
Уже пифагорийцы знали, что квадрат гипотенузы равен сумме квадратов катетов.
Знали, что когда сторона квадрата равна 1, то его диагональ должна выражаться таким числом, квадрат которого равен 2. А среди рациональных чисел такого числа не существует. Они не догадались ввести иррациональные числа и сделали вывод: если сторона квадрата 1, то длина его диагонали не равна никакому числу!!! ТО есть, существуют отрезки, которые не имеют длины!!! Это привело к кризису математической науки, который длился много столетий, пока ученые не ввели иррациональные числа. Значит, иррациональные числа – бесконечные непериодические десятичные
дроби. √2≈1,41421356… π≈3,1415926…
Бесконечные десятичные дроби
периодические непериодические
Рациональные числа иррациональные числа
дроби. √2≈1,41421356… π≈3,1415926…
Бесконечные десятичные дроби
периодические непериодические
Рациональные числа иррациональные числа
Слайд 12Действительные числа
Множество всех рациональных и иррациональных чисел називают множеством действительных чисел.
Множество обозначають буквой R , от английского слова Real, немецкого Reel – действительный. Некоторые элементы этого множества принадлежат лишь множеству действительных чисел, однако есть такие, которые приналежат множеству рациональных чисел.
Тогда,N Z Q R.Поскольку каждая точка числовой прямой определяет некоторое действительное число и, наоборот, каждое действительное число имеет место на числовой прямой, то множество действительных чисел R образуют числовую прямую.
N
1 2 3 4 …
Z
-2 -1 0 1 2 3 4 …
Q
-2 -1 0 1 2 3 4 …
R
-∞ -2 -1 0 1 2 3 4 +∞
Тогда,N Z Q R.Поскольку каждая точка числовой прямой определяет некоторое действительное число и, наоборот, каждое действительное число имеет место на числовой прямой, то множество действительных чисел R образуют числовую прямую.
N
1 2 3 4 …
Z
-2 -1 0 1 2 3 4 …
Q
-2 -1 0 1 2 3 4 …
R
-∞ -2 -1 0 1 2 3 4 +∞