- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Радианная мера угла. Поворот точки
Содержание
- 1. Радианная мера угла. Поворот точки
- 2. ОПРЕДЕЛЕНИЕ. РАДИАНОМ НАЗЫВАЕТСЯ ВЕЛИЧИНА ЦЕНТРАЛЬНОГО УГЛА, КОТОРЫЙ
- 3. Из скольких дуг, длиной R, состоит окружность?Подсказка:
- 4. Задание 1. Вывести правила перевода из радианной
- 5. ОПРЕДЕЛЕНИЕ. ОКРУЖНОСТЬ С ЦЕНТРОМ В НАЧАЛЕ СИСТЕМЫ
- 6. 01032π6ππ2πух1–π–πПроследите за одновременным движением точки на координатной
- 7. ТАК КАК ДУГИ – ЭТО ЧАСТИ ОКРУЖНОСТИ,
- 8. НАПОМНИМ, ЧТО ДЕКАРТОВА СИСТЕМА РАЗБИВАЕТСЯ КООРДИНАТНЫМИ ОСЯМИ
- 9. Слайд 9
- 10. Слайд 10
- 11. ГРАФИКИ ФУНКЦИЙ Y=X И Y=−X − ПРЯМЫЕ,
- 12. ОТМЕТИМ НА ТРИГОНОМЕТРИЧЕСКОЙ ОКРУЖНОСТИ ТОЧКУ А, СООТВЕТСТВУЮЩУЮ
- 13. ИТОГОМ НАШЕЙ ПРЕДЫДУЩЕЙ РАБОТЫ ЯВЛЯЕТСЯ ДАННАЯ ОКРУЖНОСТЬ,
- 14. ОТВЕТЫ И РЕШЕНИЯЗадание 2.
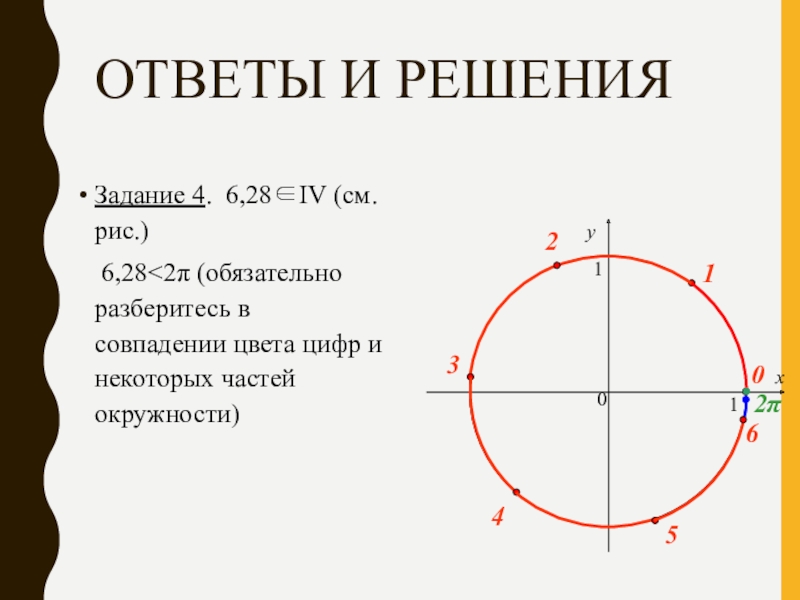
- 15. ОТВЕТЫ И РЕШЕНИЯЗадание 4. 6,28∈IV (см.рис.) 6,28
- 16. ОТВЕТЫ И РЕШЕНИЯЗадание 5.
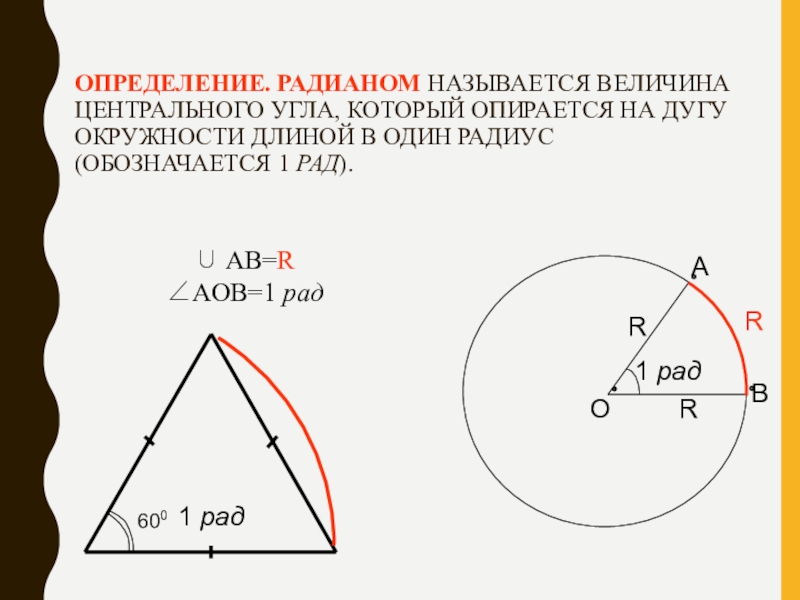
Слайд 2ОПРЕДЕЛЕНИЕ. РАДИАНОМ НАЗЫВАЕТСЯ ВЕЛИЧИНА ЦЕНТРАЛЬНОГО УГЛА, КОТОРЫЙ ОПИРАЕТСЯ НА ДУГУ ОКРУЖНОСТИ
1 рад
R
R
R
A
B
O
⋅
⋅
⋅
∪ AB=R
∠AOB=1 рад
600
1 рад
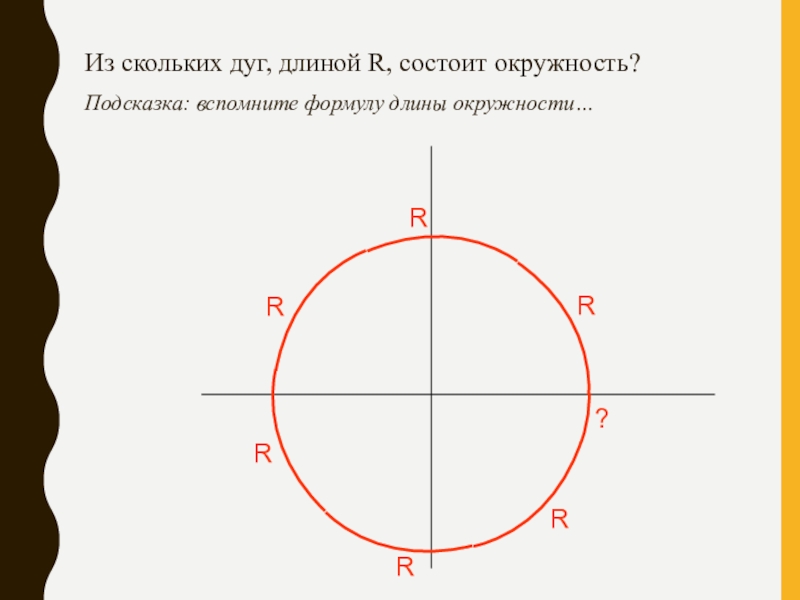
Слайд 3Из скольких дуг, длиной R, состоит окружность?
Подсказка: вспомните формулу длины окружности…
R
R
R
R
R
R
?
Слайд 4Задание 1. Вывести правила перевода из радианной меры в градусную и
Ответ: α0= α0· рад правило перевода из градусной меры в радианную;
α рад= α· правило перевода из радианной меры в градусную.
1 рад = ; 1 рад ≈ 57019’
10 = рад; 10 ≈ 0,017 рад
3600 – 2π рад
10 – х рад
3600 – 2π рад
х 0 – 1 рад
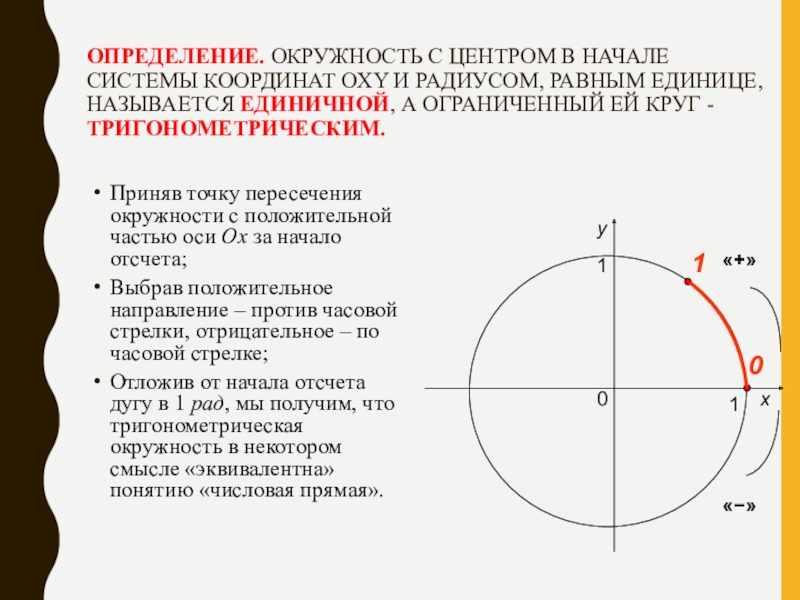
Слайд 5ОПРЕДЕЛЕНИЕ. ОКРУЖНОСТЬ С ЦЕНТРОМ В НАЧАЛЕ СИСТЕМЫ КООРДИНАТ OXY И РАДИУСОМ,
Приняв точку пересечения окружности с положительной частью оси Ох за начало отсчета;
Выбрав положительное направление – против часовой стрелки, отрицательное – по часовой стрелке;
Отложив от начала отсчета дугу в 1 рад, мы получим, что тригонометрическая окружность в некотором смысле «эквивалентна» понятию «числовая прямая».
x
y
0
1
1
0
«+»
«−»
1
Слайд 6
0
1
0
3
2π
6
π
π
2π
у
х
1
–π
–π
Проследите за одновременным движением точки на координатной прямой и на тригонометрической
Обязательно разберитесь, почему на прямой семь точек, а на окружности их пять.
Слайд 7ТАК КАК ДУГИ – ЭТО ЧАСТИ ОКРУЖНОСТИ, ТО ДЛИНЫ НЕКОТОРЫХ ИЗ
Откладывая в положительном и отрицательном направлениях от начала отсчета прямой угол получим точки, соответствующие числам …
и (объясните почему);
Выполнив поворот на развернутый угол в положительном и отрицательном направлениях получаем две совпадающие точки окружности с координатами…
и .
x
y
0
1
1
0
1
Слайд 8НАПОМНИМ, ЧТО ДЕКАРТОВА СИСТЕМА РАЗБИВАЕТСЯ КООРДИНАТНЫМИ ОСЯМИ НА ЧЕТЫРЕ КООРДИНАТНЫЕ ЧЕТВЕРТИ
Задание 2. Определите границы координатных четвертей через углы поворота в радианной мере, взятых в положительном направлении.
Задание 3. Выполните предыдущее задание, при условии, что выбирается отрицательное направление углов поворота.
Задание 4. Какой координатной четверти принадлежит точка окружности с координатой 6,28?
x
y
0
1
1
0
1
I
II
III
IV
Слайд 9 − ЭТО
Отметив на окружности точки с абсциссой 0,5 мы получим точки, соответствующие числам …
и
Аналогично, получаются точки окружности с координатами
; .
Обратите внимание на симметричность относительно оси Ox полученных точек.
x
y
0
1
1
0
1
0,5
− 0,5
Слайд 10 − ЭТО
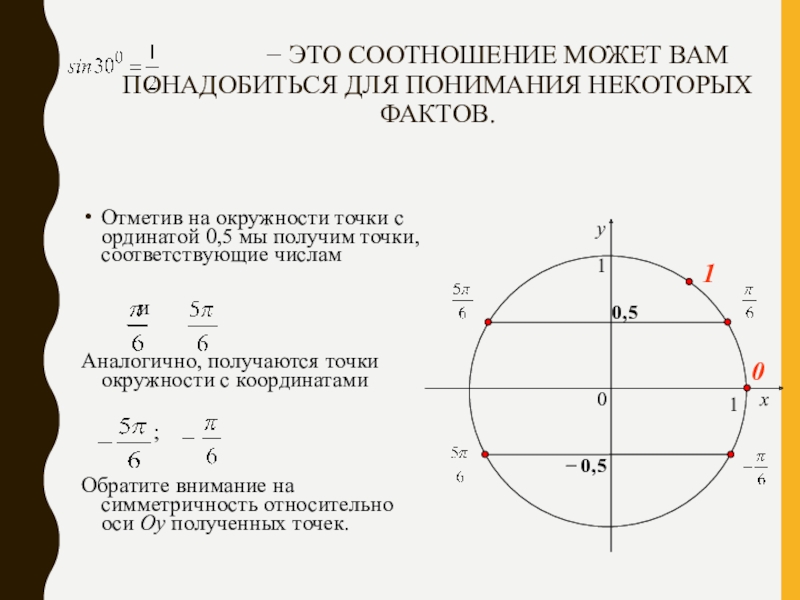
Отметив на окружности точки с ординатой 0,5 мы получим точки, соответствующие числам
и
Аналогично, получаются точки окружности с координатами
;
Обратите внимание на симметричность относительно оси Oy полученных точек.
x
y
0
1
1
0
1
0,5
− 0,5
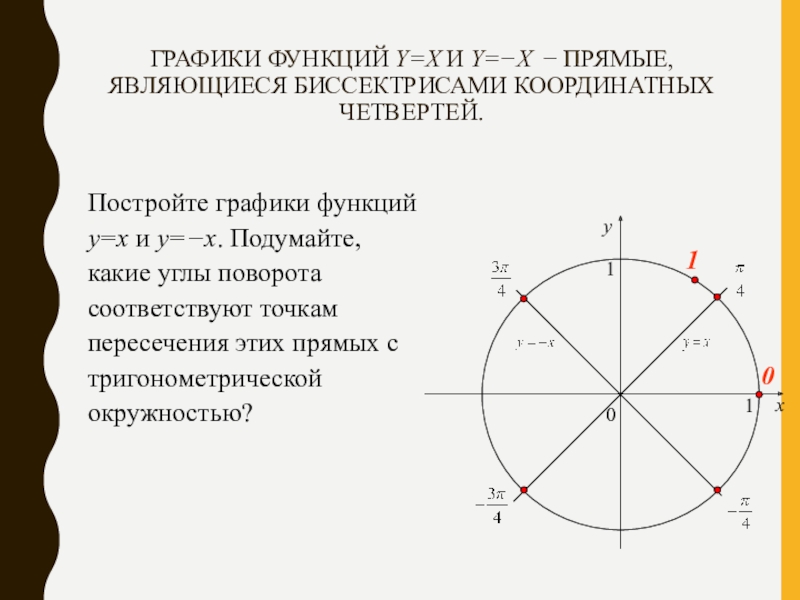
Слайд 11ГРАФИКИ ФУНКЦИЙ Y=X И Y=−X − ПРЯМЫЕ, ЯВЛЯЮЩИЕСЯ БИССЕКТРИСАМИ КООРДИНАТНЫХ ЧЕТВЕРТЕЙ.
Постройте графики функций y=x и y=−x. Подумайте, какие углы поворота соответствуют точкам пересечения этих прямых с тригонометрической окружностью?
x
y
0
1
1
0
1
Слайд 12ОТМЕТИМ НА ТРИГОНОМЕТРИЧЕСКОЙ ОКРУЖНОСТИ ТОЧКУ А, СООТВЕТСТВУЮЩУЮ ПРОИЗВОЛЬНОМУ ОСТРОМУ ПОЛОЖИТЕЛЬНОМУ УГЛУ
Если добавить полный поворот к углу α , то мы снова окажемся в той же точке А. Но теперь ее координата равна (подумайте)… .
Вообще, любую точку окружности можно получить поворотом на угол, вида α+2πn, где n∈Ζ и α∈[0;2π).
x
y
0
1
1
0
A(α)
A(α+2π)
Слайд 13ИТОГОМ НАШЕЙ ПРЕДЫДУЩЕЙ РАБОТЫ ЯВЛЯЕТСЯ ДАННАЯ ОКРУЖНОСТЬ, НА КОТОРОЙ ОТМЕЧЕНЫ НАИБОЛЕЕ
Примечание. На чертеже отмечены только положительные углы поворота.
Задание 5. Найдите координаты всех точек, отмеченных на данной окружности (указание: рассмотрите различные прямоугольные треугольники с гипотенузой-радиусом (см. рис.) и примените теорему Пифагора ; помните о симметричности точек).
x
y
0
1
1
0
1
0,5
0,5
-0,5
-0,5
Слайд 14ОТВЕТЫ И РЕШЕНИЯ
Задание 2. - I четверть,
- III четверть, - IV четверть.
Задание 3. - I четверть, - II четверть,
- III четверть, - IV четверть
Слайд 15ОТВЕТЫ И РЕШЕНИЯ
Задание 4. 6,28∈IV (см.рис.)
6,28
x
y
0
1
1
0
1
2
3
4
5
6
2π