Максим,
Беловодский Антон.
Руководитель (консультант):преподаватель математики Ковалева В.С.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Производная и её применение
Содержание
- 1. Производная и её применение
- 2. БЕЛГОРОД
- 3. ПроблемаДля мойки автомобилей требуется изготовить открытый цилиндрический
- 4. Определение функцииЕсли каждому значению хиз некоторого множества
- 5. Вывод: до 500км выгодней заказ у второй
- 6. Слайд 6
- 7. Экономические расчетыЗадача: Стоимость оборудования мастерской равна 500
- 8. Решение. где B = 200 тыс. рублей,
- 9. Г. ЛейбницИ. Ньютон Основоположники дифференциального исчисления
- 10. Ньютон.задача о скорости движения материальной точки в
- 11. Понятие производной Механический смысл производной
- 12. Средняя скорость движения∆t ∆S
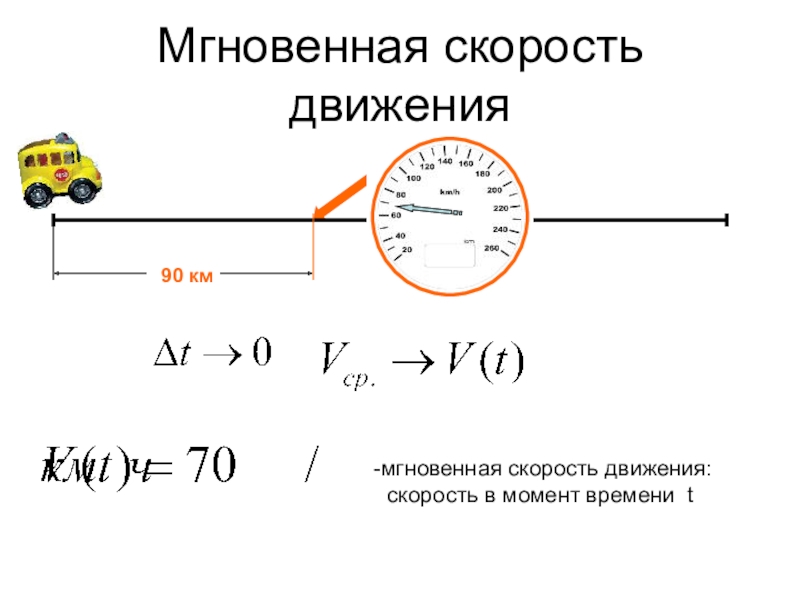
- 13. Мгновенная скорость движения90 кммгновенная скорость движения: скорость в момент времени t
- 14. Мгновенная скорость движенияПредел разностного отношения при
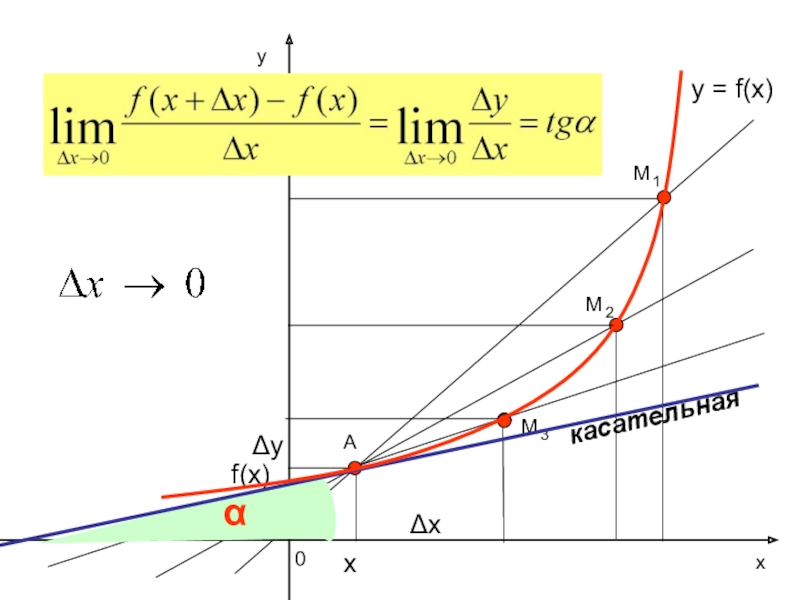
- 15. Геометрический смысл производнойГотфрид Вильгельм ЛейбницРешение задач
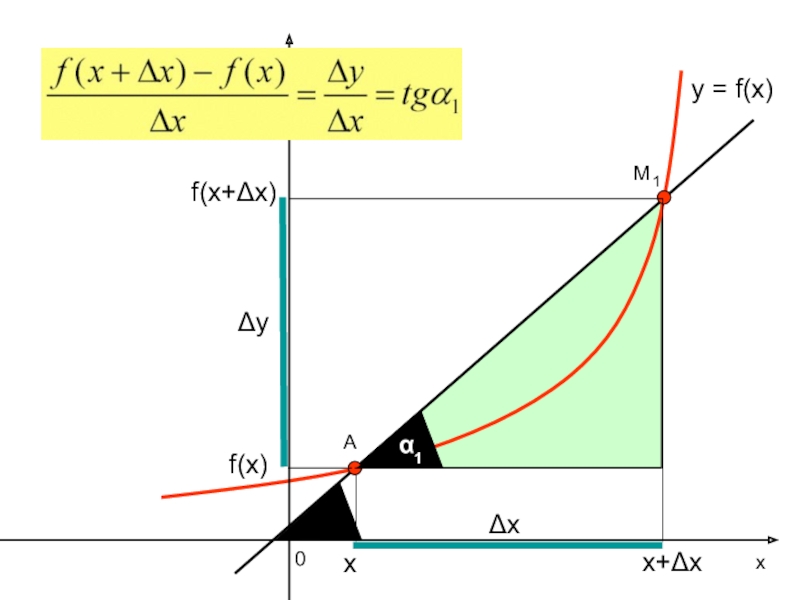
- 16. ух0y = f(x)АΔхΔуf(x)f(x+Δх)х+Δхх
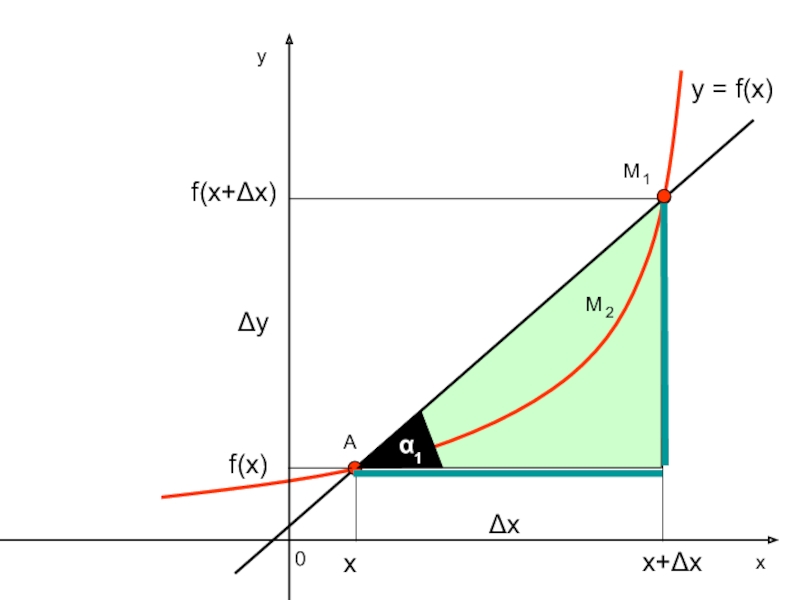
- 17. ух0y = f(x)АΔхΔуf(x)f(x+Δх)х+Δхх
- 18. ух0y = f(x)АΔхΔуf(x)f(x+Δх)х+Δхх
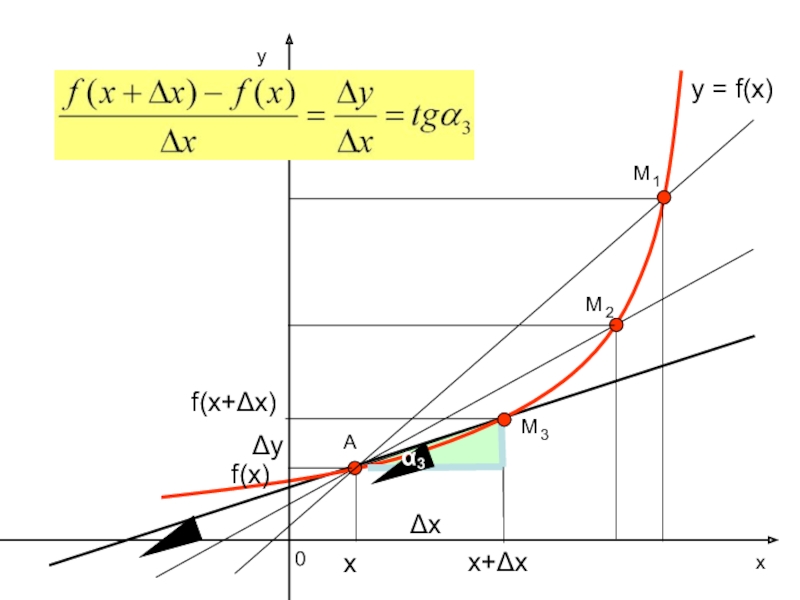
- 19. ух0y = f(x)АΔхΔуf(x)хαкасательная
- 20. Угловой коэффициент касательной- производная функции в данной точке
- 21. производной функции у = f(x) в точке
- 22. Применение производной в решении экстремальных задачНеобходимое условие
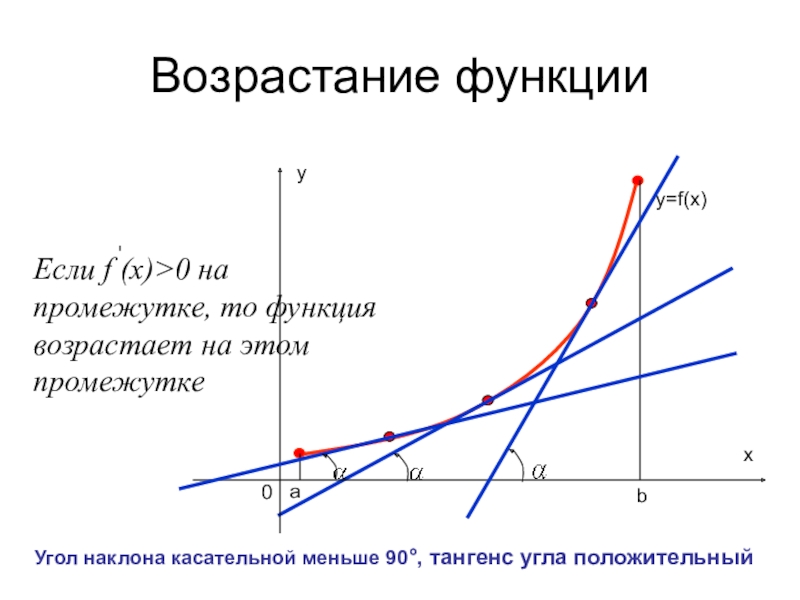
- 23. аbВозрастание функцииy=f(x)Угол наклона касательной меньше 90°, тангенс угла положительный
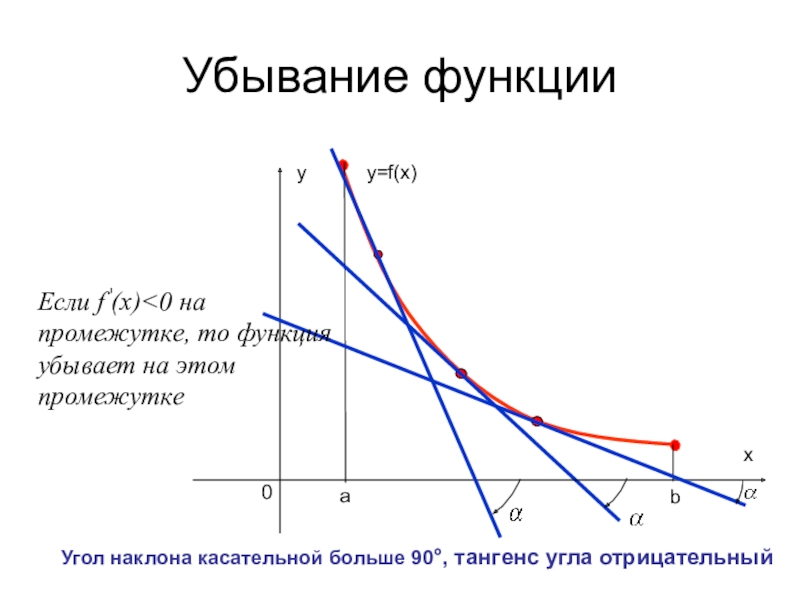
- 24. аbУбывание функцииy=f(x)Угол наклона касательной больше 90°, тангенс угла отрицательный
- 25. Экстремумы функций
- 26. Максимум функцииf(х)y=f(x)Точка х0 –точка максимумафункции f(x), если
- 27. Минимум функцииf(х)y=f(x)Точка х0 –точка минимумафункции f(x), если
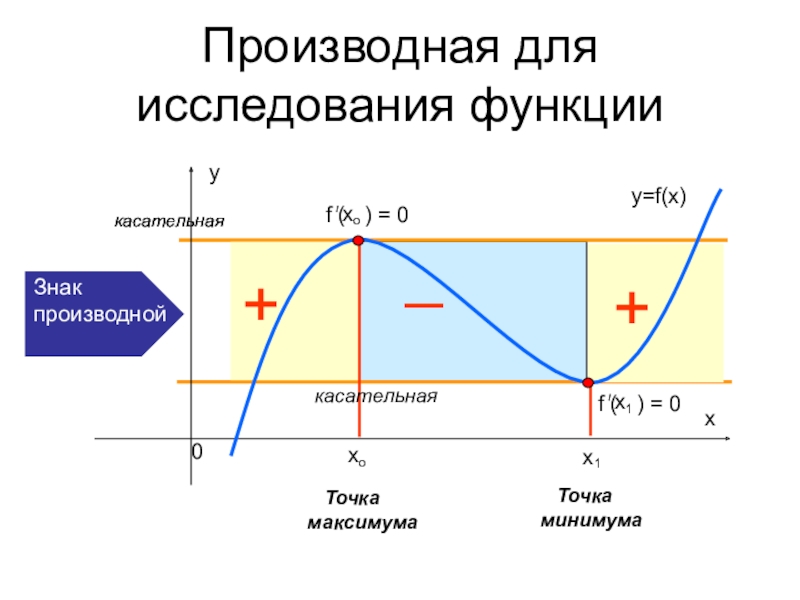
- 28. Производная для исследования функции_ Точка максимума Точка минимумакасательнаякасательнаякасательная
- 29. Наибольшим ( наименьшим)значением функции называется самое большое
- 30. Задачи на максимум и минимум
- 31. Основные моменты решения нашей задачи с помощью
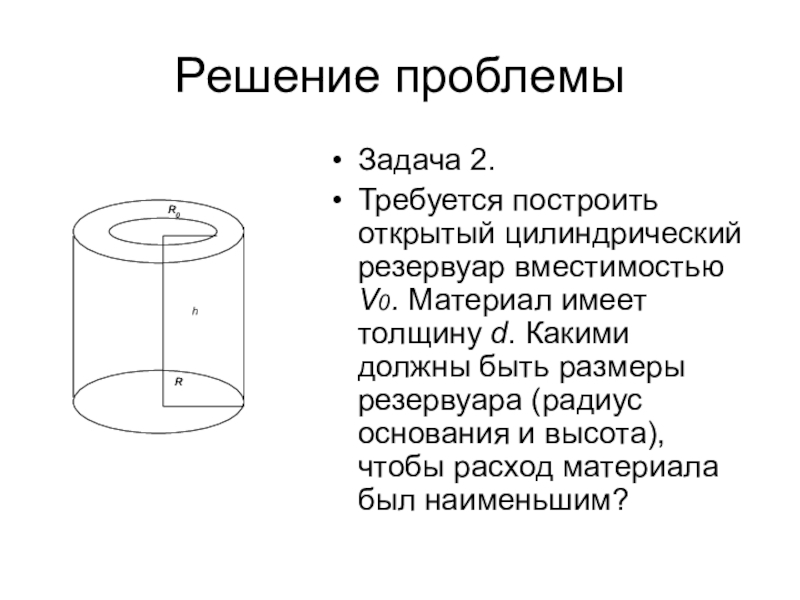
- 32. Решение проблемыЗадача 2.Требуется построить открытый цилиндрический резервуар
- 33. Пусть - внутренний объем цилиндра, высотой h.
- 34. Найдем точки, в которых производная равна нулю
- 35. Получили: чтобы изготовить цилиндрический резервуар объемом V0
- 36. Пусть h=R=x, тогда получаем: Значит, h=R=4,57дм,
- 37. Следи, чтобы автомобиль был исправным!Исключи утечку топлива
- 38. БЕЛГОРОДБелгород должен быть чистым!
- 39. Литература и другие источники: Башмаков М. И.
БЕЛГОРОД
Слайд 1Учебно-исследовательская работа
«Функция и её производная
в решении практических задач»
Подготовили:
учащиеся гр.№24
Терещенко
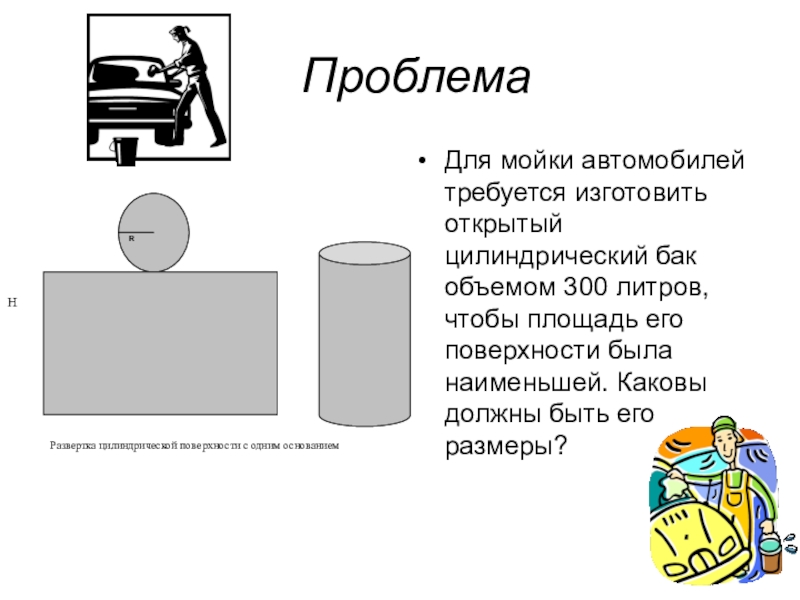
Слайд 3Проблема
Для мойки автомобилей требуется изготовить открытый цилиндрический бак объемом 300 литров,
чтобы площадь его поверхности была наименьшей. Каковы должны быть его размеры?
Слайд 4
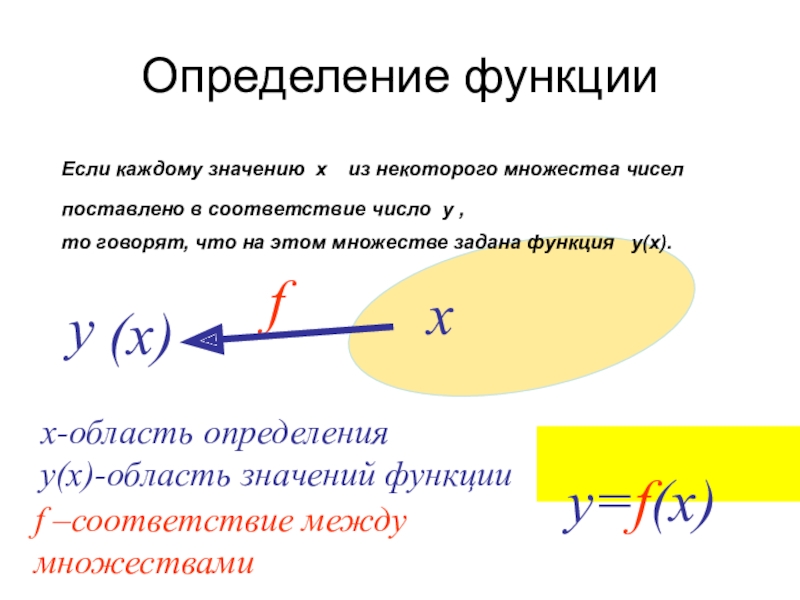
Определение функции
Если каждому значению х
из некоторого множества чисел
поставлено в соответствие число
у ,
то говорят, что на этом множестве задана функция у(х).
f
х
у
(х)
x-область определения
y(x)-область значений функции
f –соответствие между множествами
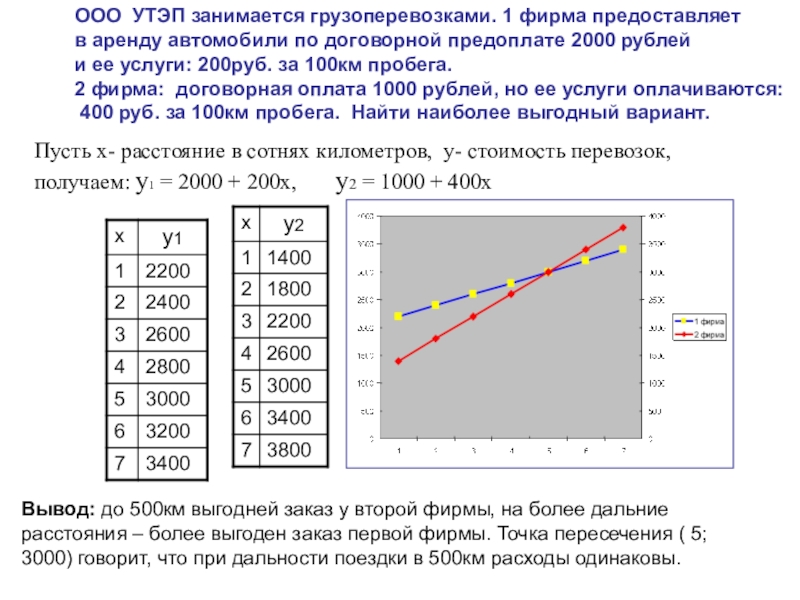
Слайд 5Вывод: до 500км выгодней заказ у второй фирмы, на более дальние
расстояния – более выгоден заказ первой фирмы. Точка пересечения ( 5; 3000) говорит, что при дальности поездки в 500км расходы одинаковы.
Пусть х- расстояние в сотнях километров, у- стоимость перевозок, получаем: у1 = 2000 + 200х, y2 = 1000 + 400х
ООО УТЭП занимается грузоперевозками. 1 фирма предоставляет
в аренду автомобили по договорной предоплате 2000 рублей
и ее услуги: 200руб. за 100км пробега.
2 фирма: договорная оплата 1000 рублей, но ее услуги оплачиваются:
400 руб. за 100км пробега. Найти наиболее выгодный вариант.
Слайд 6
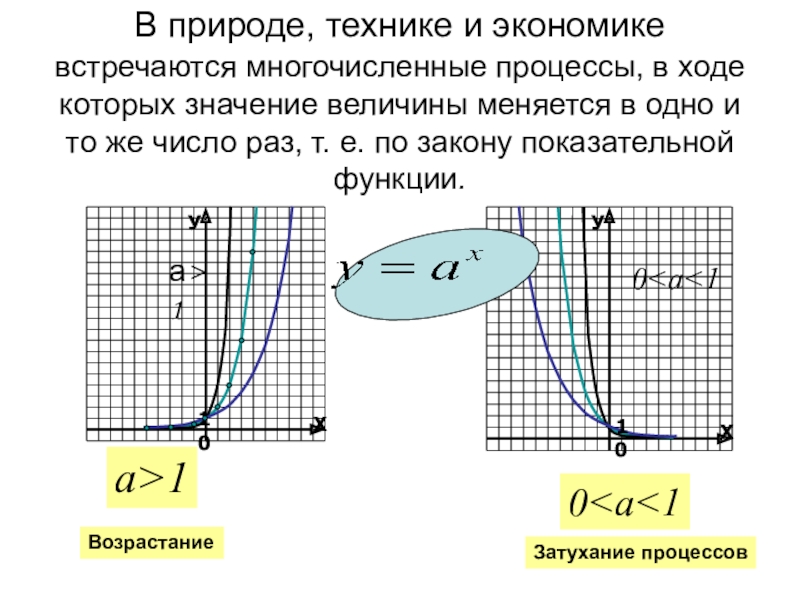
0
значение величины меняется в одно и то же число раз, т. е. по закону показательной функции.
Возрастание
Затухание процессов
Слайд 7Экономические расчеты
Задача: Стоимость оборудования мастерской равна 500 тыс. р. Известно, что
через 10 лет стоимость этого оборудования вследствие амортизации будет равна 200 тыс. р. Найдите процент ежегодной амортизации оборудования.
завод
Слайд 8Решение.
где B = 200 тыс. рублей,
тыс. рублей, x
= 10 лет.
Ответ:
ежегодный процент амортизации составляет 8,76 %.
Слайд 10Ньютон.
задача о скорости движения материальной точки в данный момент времени (мгновенной
скорости).
Лейбниц
задача о построении касательной к любой кривой, заданной своим уравнением.
Основоположники дифференциального исчисления
Слайд 14Мгновенная скорость движения
Предел разностного отношения при
называется
производной функции S(t). Обозначается
производной функции S(t). Обозначается
Мгновенная скорость – производная пути по времени
Слайд 15
Геометрический смысл производной
Готфрид Вильгельм Лейбниц
Решение задач на нахождение углового коэффициента касательной
имеет большое значение. Ведь скорость движущейся точки направлена по касательной к её траектории.
поэтому определение скорости снаряда на его траектории, скорости любой планеты на её орбите сводится, к определению направления касательной к кривой.
поэтому определение скорости снаряда на его траектории, скорости любой планеты на её орбите сводится, к определению направления касательной к кривой.
Слайд 21производной функции у = f(x) в точке х0
называется предел отношения
приращения функции в точке х0
к приращению аргумента,
когда приращение аргумента
стремится к нулю.
Слайд 22Применение производной в решении экстремальных задач
Необходимое условие экстремума.
Теорема Ферма. Если
является точкой экстремума функции и производная в этой точке существует, то она равна нулю: .
Слайд 26
Максимум функции
f(х)
y=f(x)
Точка х0 –точка максимума
функции f(x), если существует
Такая окрестность точки х0,
что для всех х≠х0, из этой
Окрестности выполняется
неравенство
Окрестности выполняется
неравенство
Точка х0 –точка максимума
функции f(x), если существует
Такая окрестность точки х0,
что для всех х≠х0, из этой
Окрестности выполняется
неравенство
Слайд 27
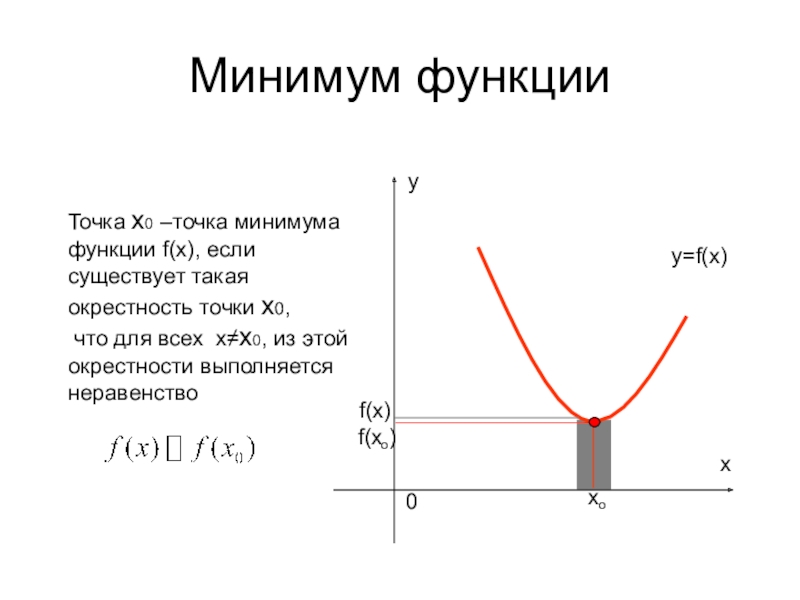
Минимум функции
f(х)
y=f(x)
Точка х0 –точка минимума
функции f(x), если существует такая окрестность точки
х0,
что для всех х≠х0, из этой
окрестности выполняется
неравенство
что для всех х≠х0, из этой
окрестности выполняется
неравенство
Слайд 28
Производная для исследования функции
_
Точка
максимума
Точка
минимума
касательная
касательная
касательная
Слайд 29Наибольшим ( наименьшим)значением функции называется самое большое значение функции ( самое
малое)из всех максимумов (минимумов), включая концы заданного для функции интервала
Слайд 31Основные моменты решения нашей задачи
с помощью производной:
1.Устанавливаем функциональную зависимость
между
заданными величинами.
2.Находим производную полученной функции.
2. Приравниваем производную к нулю и определяем
все критические точки из области определения функции.
3. Устанавливают знаки производной функции
при переходе через критические точки .
4.Определяем точки экстремума.
5. Вычисляют значения функции в каждой экстремальной точке.
6. Выбираем наименьшее значение из всех минимумов,
включая концы интервала
2.Находим производную полученной функции.
2. Приравниваем производную к нулю и определяем
все критические точки из области определения функции.
3. Устанавливают знаки производной функции
при переходе через критические точки .
4.Определяем точки экстремума.
5. Вычисляют значения функции в каждой экстремальной точке.
6. Выбираем наименьшее значение из всех минимумов,
включая концы интервала
Слайд 32Решение проблемы
Задача 2.
Требуется построить открытый цилиндрический резервуар вместимостью V0. Материал имеет
толщину d. Какими должны быть размеры резервуара (радиус основания и высота), чтобы расход материала был наименьшим?
Слайд 33Пусть
- внутренний объем цилиндра, высотой h.
V
- объем внешнего цилиндра, высотой h.
=
=
.
Объем дна:
Объем материала: Vмат. = (V-V0)+Vдна
Получили функциональную зависимость между объемом и высотой цилиндра.
Выразим
Слайд 34
Найдем точки, в которых производная равна нулю или не существует.
Эти
точки называются критическими для функции
.
,
Единственный положительный корень производной – это точка,
она и дает решение задачи. Так как
, то
.
Х –радиус внутреннего цилиндра. Значит, высота цилиндра
и внутренний радиус должны быть равны!
Слайд 35Получили: чтобы изготовить цилиндрический резервуар объемом V0 при наименьшем расходе материала
высота цилиндра и радиус внутреннего цилиндра должны быть равны, от толщины материала полученное решение задачи не зависит.
Используя решение этой задачи, получаем: чтобы изготовить открытый цилиндрический бак объемом 300 л наименьшей площади его поверхности необходимо, чтобы радиус и высота цилиндра были равны.
Используя решение этой задачи, получаем: чтобы изготовить открытый цилиндрический бак объемом 300 л наименьшей площади его поверхности необходимо, чтобы радиус и высота цилиндра были равны.
Слайд 36Пусть h=R=x, тогда
получаем:
Значит, h=R=4,57дм, а площадь
поверхности
Чтобы изготовить открытый цилиндрический бак
объемом 300 литров наименьшей площади поверхности,
его радиус и высота должны быть h=R=4,57дм.
ВЫВОД:
Слайд 37
Следи, чтобы автомобиль был исправным!
Исключи утечку топлива и смазки!
Следи за герметичностью
узлов и систем агрегатов!
Используй только качественное горючее!
Установи нейтрализаторы на выхлоп!
При ТО не разливай ГСМ!
Не выбрасывай использованную ветошь!
Отработанное масло слей и отправь на переработку!
Используй только качественное горючее!
Установи нейтрализаторы на выхлоп!
При ТО не разливай ГСМ!
Не выбрасывай использованную ветошь!
Отработанное масло слей и отправь на переработку!
Слайд 39Литература и другие источники: Башмаков М. И. «Алгебра и начала анализа 10-11».
М.: Просвещение, 1992.
Беляева Э. С., Монахов В.М. «Экстремальные задачи». М.: Просвещение, 1997.
Виленкин Н. Л. «Функции в природе и технике». – М.: Просвещение, 1978
Возняк Г. М., Гусев В. А. Прикладные задачи на экстремумы. М.: Просвещение, 1985.
Математика в жизни общества - http://revolution.allbest.ru/mathematics/l
images.yandex.ru›белгород фото города
