- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Производная( 10 класс )
Содержание
- 1. Производная( 10 класс )
- 2. Повторим теориюПроизводная в заданной точке хо (число)
- 3. Геометрический смысл производнойЗадача: На рисунке изображён
- 4. ααФункция возрастает α - угол наклона
- 5. Промежутки возрастания и убывания –
- 6. Исследование экстремумов функции Необходимое условие экстремума
- 7. Теорема Ферма лишь необходимое условие
- 8. Достаточные условия существования экстремума в точкеПризнак максимума
- 9. Достаточные условия существования экстремума в точкеПризнак минимума
- 10. Функция y=f(x) задана на промежутке (a;b). На
- 11. Функция y=f(x) задана на промежутке (a;b). На
- 12. В 8
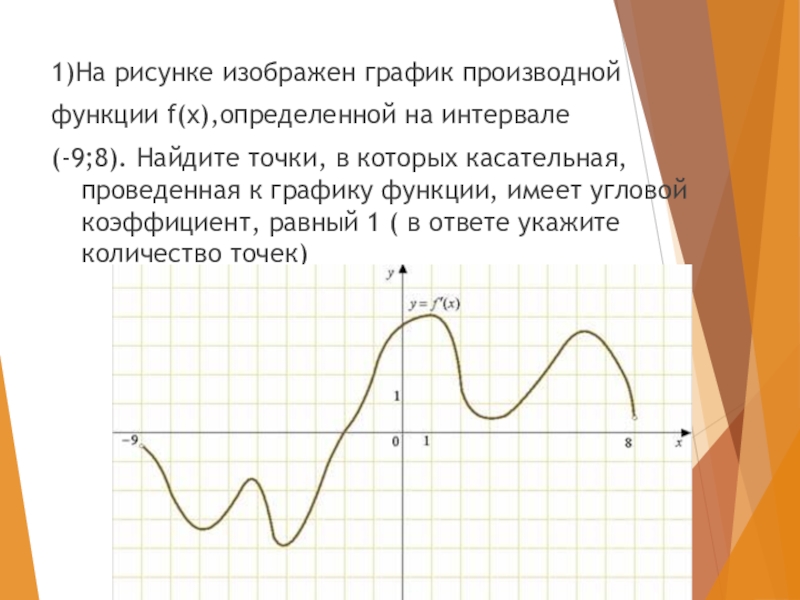
- 13. 1)На рисунке изображен график производнойфункции f(x),определенной на
- 14. 1)На рисунке изображен график производнойфункции f(x),определенной на
- 15. Ответ: 6
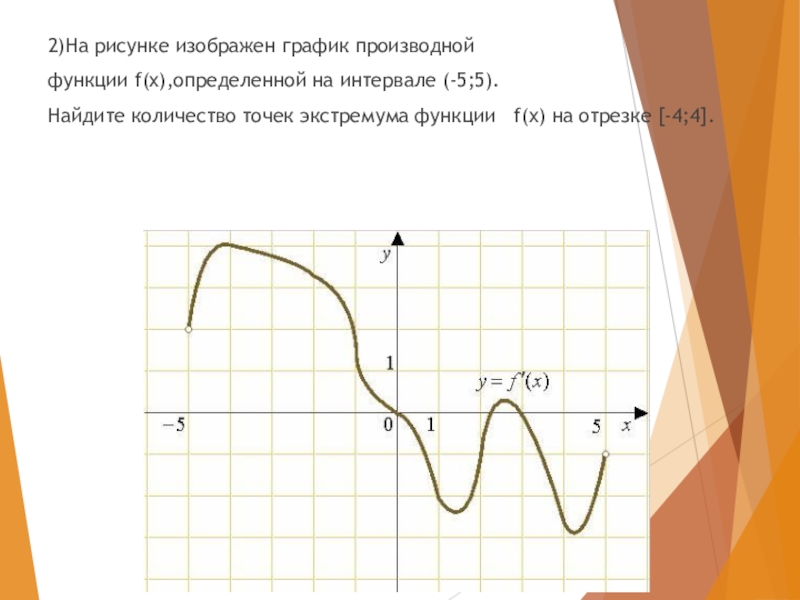
- 16. 2)На рисунке изображен график производнойфункции f(x),определенной на
- 17. Ответ: 3
- 18. 3)На рисунке изображен график производнойфункции f(x),определенной на
- 19. Ответ: -1
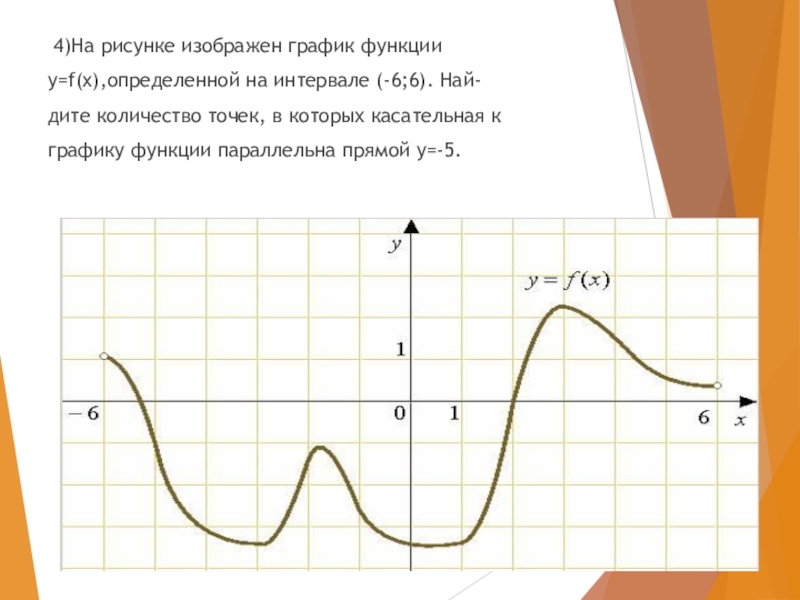
- 20. 4)На рисунке изображен график функцииy=f(x),определенной на
- 21. Ответ: 4
- 22. 5)На рисунке изображен график производнойфункции f(x),определенной на
- 23. Ответ: -4
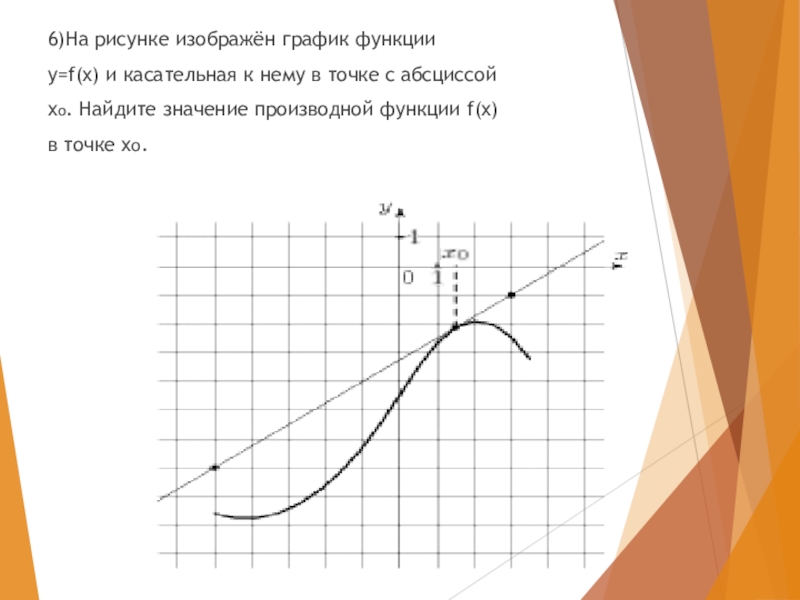
- 24. 6)На рисунке изображён график функцииy=f(x) и касательная
- 25. Ответ: 0.75
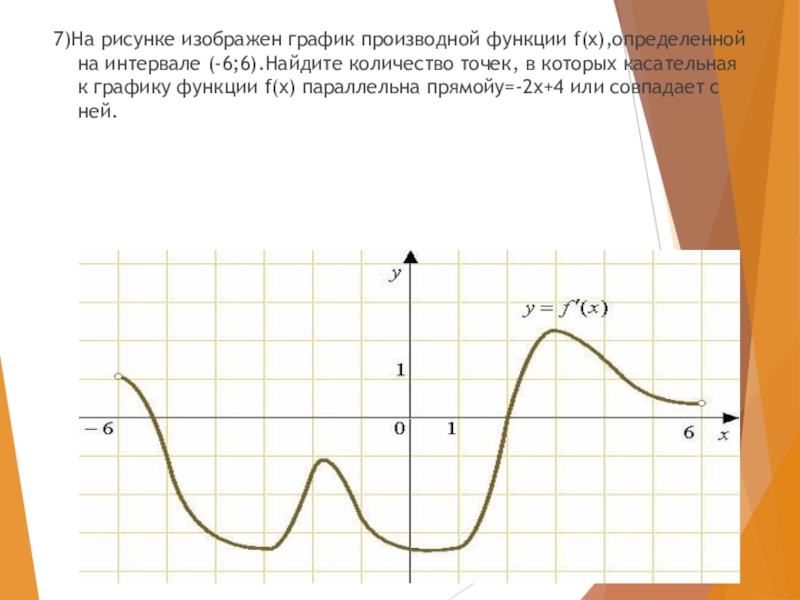
- 26. 7)На рисунке изображен график производной функции
- 27. Ответ: 4
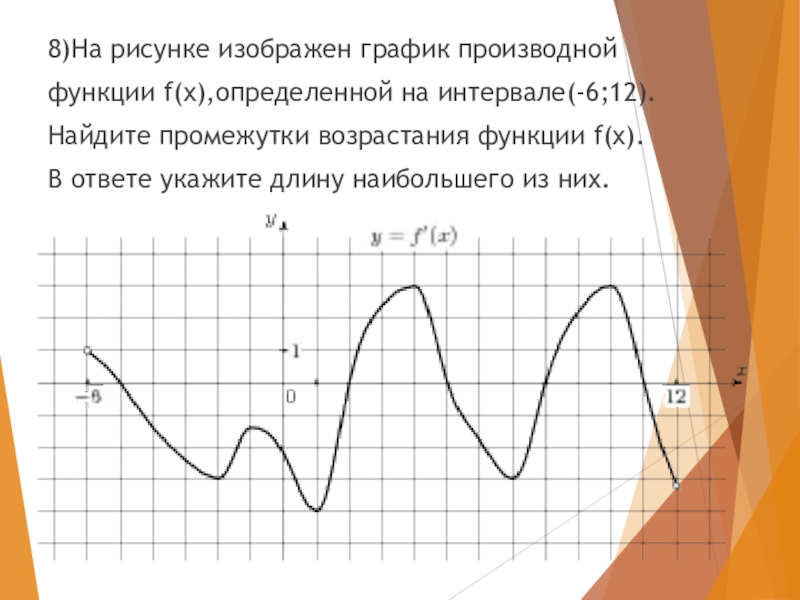
- 28. 8)На рисунке изображен график производнойфункции f(x),определенной на
- 29. Ответ: 3
- 30. 9)Прямая y=8x-5 параллельнакасательной к графику функцииy=x²+7x+7.Найдите абсциссу точ-ки касания.
- 31. Слайд 31
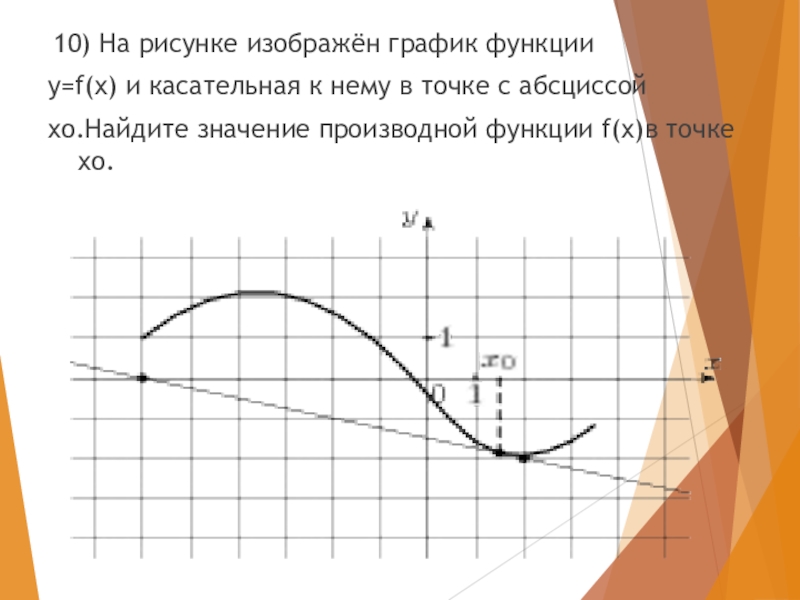
- 32. 10) На рисунке изображён график функцииy=f(x)
- 33. Ответ: -0.25
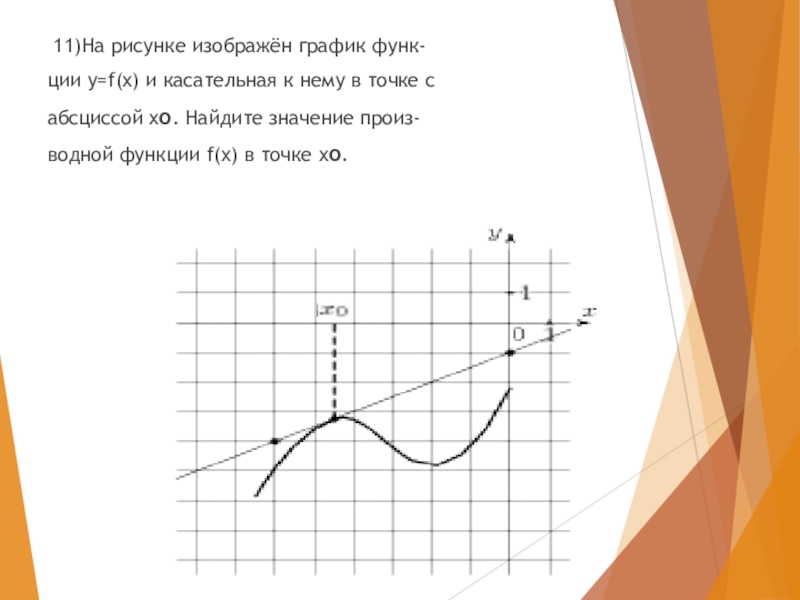
- 34. 11)На рисунке изображён график функ-ции y=f(x)
- 35. Слайд 35
Повторим теориюПроизводная в заданной точке хо (число) = тангенс угла наклона касательной (проведенной к графику функции в заданной точке хо)= угловой коэффициент касательной По значению производной (числу) можно сделать вывод о следующих свойствах функции :монотонности (возрастании,
Слайд 2Повторим теорию
Производная в заданной точке хо (число) = тангенс угла наклона
касательной (проведенной к графику функции в заданной точке хо)= угловой коэффициент касательной
По значению производной (числу) можно сделать вывод
о следующих свойствах функции :
монотонности (возрастании, убывании);
наличии точек экстремума функции (точек максимума,
минимума, то есть критических точек)
Определить , чему равен угловой коэффициент
касательной, проведенной к графику функции в
заданной точке (другими словами «тангенс угла наклона
касательной»)
По значению производной (числу) можно сделать вывод
о следующих свойствах функции :
монотонности (возрастании, убывании);
наличии точек экстремума функции (точек максимума,
минимума, то есть критических точек)
Определить , чему равен угловой коэффициент
касательной, проведенной к графику функции в
заданной точке (другими словами «тангенс угла наклона
касательной»)
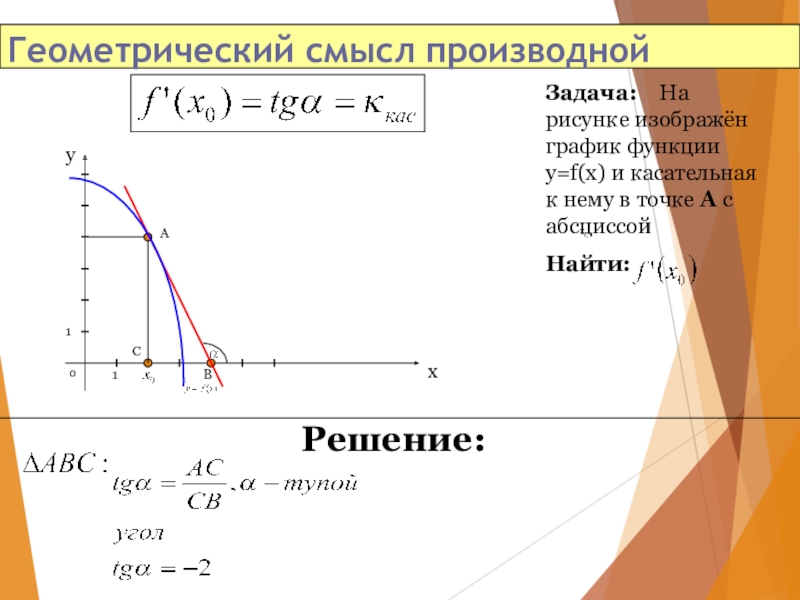
Слайд 3Геометрический смысл производной
Задача: На рисунке изображён график функции y=f(x) и
касательная к нему в точке А с абсциссой
Найти:
Найти:
Решение:
у
х
0
1
1
В
А
С
Слайд 4
α
α
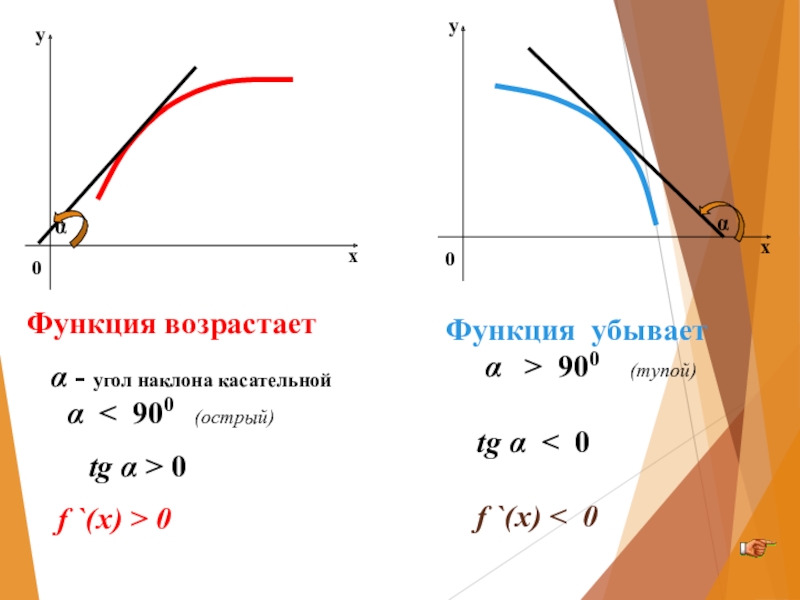
Функция возрастает
α - угол наклона касательной
α < 900 (острый)
tg α > 0
f `(x) > 0
tg α > 0
f `(x) > 0
Функция убывает
α > 900 (тупой)
tg α < 0
f `(x) < 0
Слайд 5 Промежутки возрастания и убывания – промежутки монотонности.
Достаточный признак убывания
: если f’ (x)< 0 (производная отрицательна), то функция f (x) убывает на данном промежутке.
Достаточный признак возрастания :
если f’ (x)> 0 (производная положительна),
то функция f (x) возрастает на
данном промежутке.
Достаточный признак возрастания :
если f’ (x)> 0 (производная положительна),
то функция f (x) возрастает на
данном промежутке.
Слайд 6Исследование экстремумов функции
Необходимое условие экстремума (теорема Ферма)
Если точка х0
является точкой экстремума функции f и в этой точке существует производная f `(x), то она равна нулю: 0
f `(x) = 0
f `(x) = 0
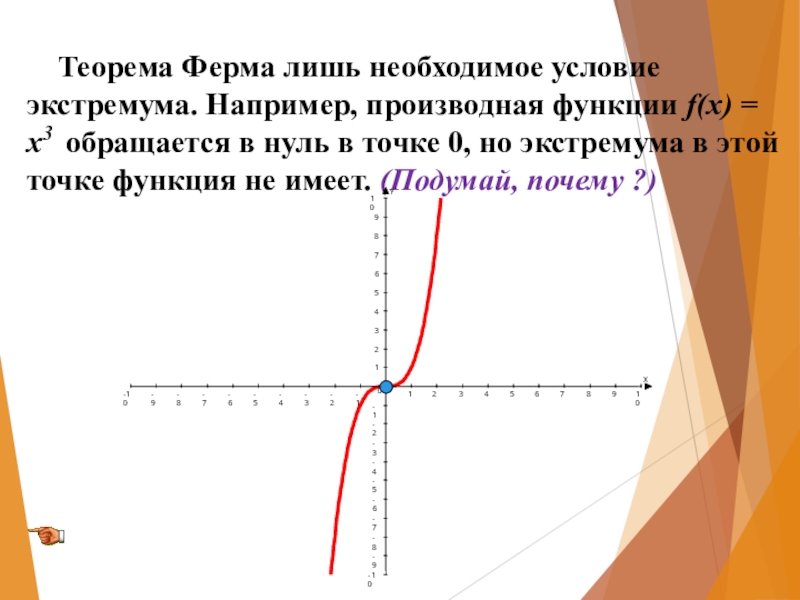
Слайд 7 Теорема Ферма лишь необходимое условие экстремума. Например, производная функции
f(x) = x3 обращается в нуль в точке 0, но экстремума в этой точке функция не имеет. (Подумай, почему ?)
0
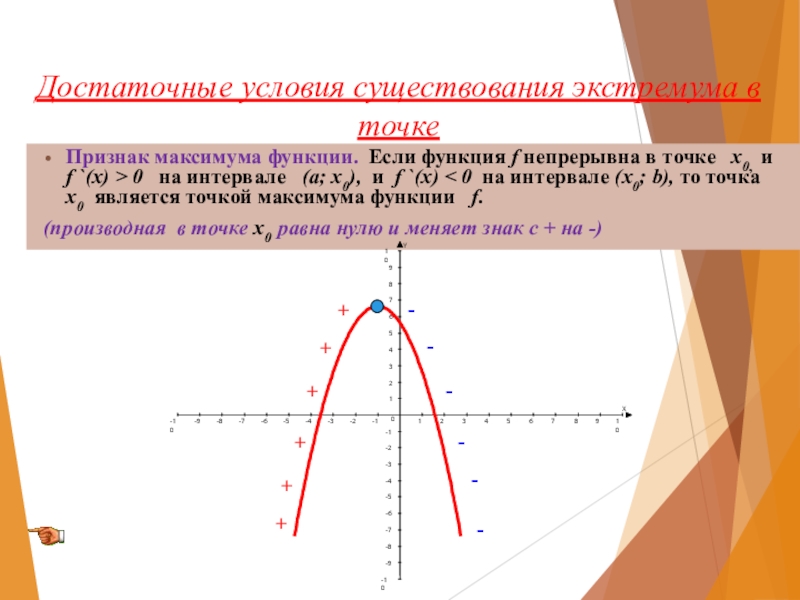
Слайд 8Достаточные условия существования экстремума в точке
Признак максимума функции. Если функция f
непрерывна в точке х0, и f `(x) > 0 на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f.
(производная в точке х0 равна нулю и меняет знак с + на -)
(производная в точке х0 равна нулю и меняет знак с + на -)
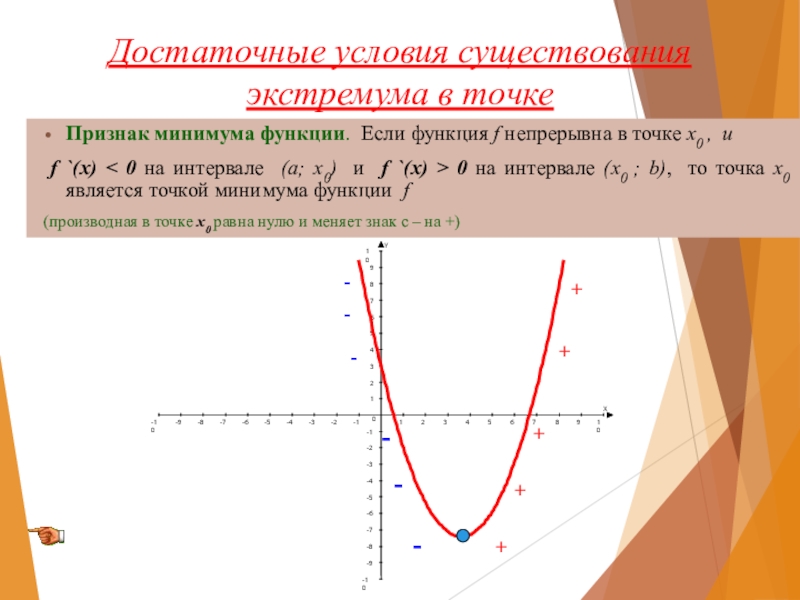
Слайд 9Достаточные условия существования экстремума в точке
Признак минимума функции. Если функция f
непрерывна в точке х0 , и
f `(x) < 0 на интервале (а; х0) и f `(x) > 0 на интервале (х0 ; b), то точка х0 является точкой минимума функции f
(производная в точке х0 равна нулю и меняет знак с – на +)
f `(x) < 0 на интервале (а; х0) и f `(x) > 0 на интервале (х0 ; b), то точка х0 является точкой минимума функции f
(производная в точке х0 равна нулю и меняет знак с – на +)
X
Y
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
0
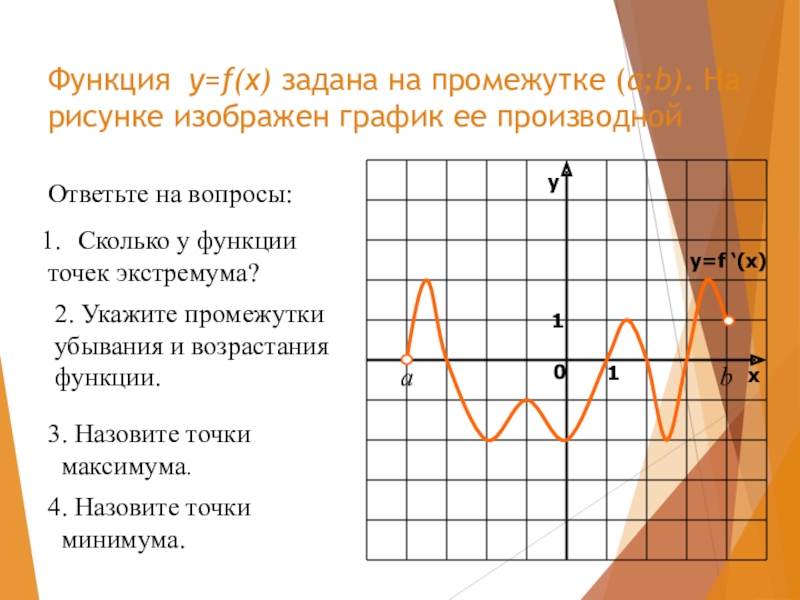
Слайд 10Функция y=f(x) задана на промежутке (a;b). На рисунке изображен график ее
производной
Ответьте на вопросы:
Сколько у функции
точек экстремума?
2. Укажите промежутки
убывания и возрастания
функции.
3. Назовите точки
максимума.
4. Назовите точки
минимума.
b
а
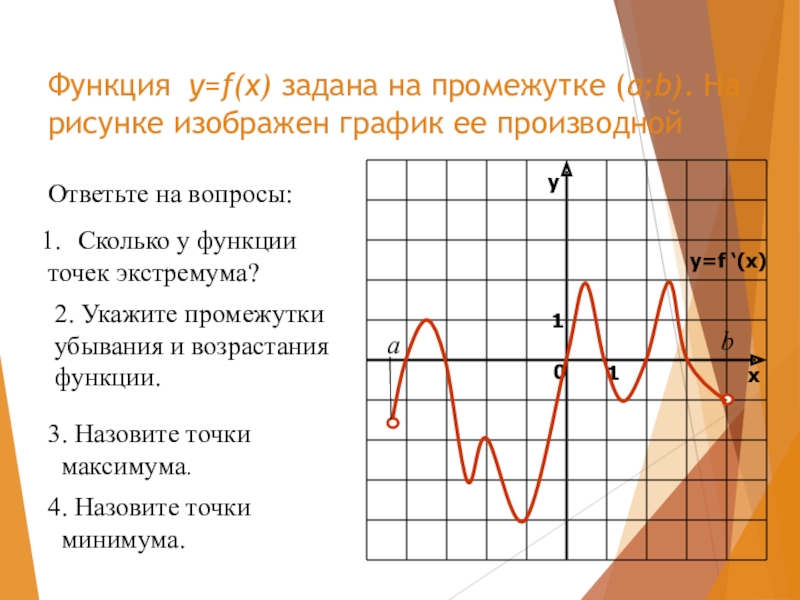
Слайд 11Функция y=f(x) задана на промежутке (a;b). На рисунке изображен график ее
производной
Ответьте на вопросы:
Сколько у функции
точек экстремума?
2. Укажите промежутки
убывания и возрастания
функции.
3. Назовите точки
максимума.
4. Назовите точки
минимума.
а
b
Слайд 13
1)На рисунке изображен график производной
функции f(x),определенной на интервале
(-9;8). Найдите точки,
в которых касательная, проведенная к графику функции, имеет угловой коэффициент, равный 1 ( в ответе укажите количество точек)
Слайд 14
1)На рисунке изображен график производной
функции f(x),определенной на интервале
(-9;8). В какой
точке отрезка [0;6] f(x) принимает наибольшее значение.
![1)На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8). В какой точке отрезка [0;6] f(x) принимает наибольшее](/img/thumbs/078695e32efb1885a1b25f7a2dcd7db5-800x.jpg "Производная( 10 класс ) 1)На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8). В какой")
Слайд 16
2)На рисунке изображен график производной
функции f(x),определенной на интервале (-5;5).
Найдите количество точек
экстремума функции f(x) на отрезке [-4;4].
Слайд 18
3)На рисунке изображен график производной
функции f(x),определенной на интервале (-5;5).
В какой точке
отрезка [-4;-1] f(x) принимает
наибольшее значение.
наибольшее значение.
![3)На рисунке изображен график производнойфункции f(x),определенной на интервале (-5;5).В какой точке отрезка [-4;-1] f(x) принимаетнаибольшее значение.](/img/thumbs/580c13f7a1b9713ba1f0f9b2294c12fd-800x.jpg "Производная( 10 класс ) 3)На рисунке изображен график производнойфункции f(x),определенной на интервале (-5;5).В какой точке")
Слайд 20
4)На рисунке изображен график функции
y=f(x),определенной на интервале (-6;6). Най-
дите количество
точек, в которых касательная к
графику функции параллельна прямой y=-5.
графику функции параллельна прямой y=-5.
Слайд 22
5)На рисунке изображен график производной
функции f(x),определенной на интервале (-9;8).
В какой точке
отрезка [-8;-4] f(x) принимает
наименьшее значение.
наименьшее значение.
![5)На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8).В какой точке отрезка [-8;-4] f(x) принимаетнаименьшее значение.](/img/thumbs/62a62e2031d5aeeba59e0b2e17f4496b-800x.jpg "Производная( 10 класс ) 5)На рисунке изображен график производнойфункции f(x),определенной на интервале (-9;8).В какой точке")
Слайд 24
6)На рисунке изображён график функции
y=f(x) и касательная к нему в точке
с абсциссой
xo. Найдите значение производной функции f(x)
в точке xo.
xo. Найдите значение производной функции f(x)
в точке xo.
Слайд 26
7)На рисунке изображен график производной функции f(x),определенной на интервале (-6;6).Найдите
количество точек, в которых касательная к графику функции f(x) параллельна прямойy=-2x+4 или совпадает с ней.
Слайд 28
8)На рисунке изображен график производной
функции f(x),определенной на интервале(-6;12).
Найдите промежутки возрастания функции
f(x).
В ответе укажите длину наибольшего из них.
В ответе укажите длину наибольшего из них.
Слайд 30
9)Прямая y=8x-5 параллельна
касательной к графику функции
y=x²+7x+7.Найдите абсциссу точ-
ки касания.
Слайд 32
10) На рисунке изображён график функции
y=f(x) и касательная к нему
в точке с абсциссой
xo.Найдите значение производной функции f(x)в точке xo.
xo.Найдите значение производной функции f(x)в точке xo.
Слайд 34
11)На рисунке изображён график функ-
ции y=f(x) и касательная к нему
в точке с
абсциссой xo. Найдите значение произ-
водной функции f(x) в точке xo.
абсциссой xo. Найдите значение произ-
водной функции f(x) в точке xo.
