модулем»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Программа и презентация к элективному курсу Уравнения и неравенства, содержащие модуль. Графики уравнений с модулем для учащихся 9 класса.
Содержание
- 1. Программа и презентация к элективному курсу Уравнения и неравенства, содержащие модуль. Графики уравнений с модулем для учащихся 9 класса.
- 2. Программа элективного курса предпрофильной подготовки расчитана НА 17 ЧАСОВ
- 3. Цели курса: рассмотреть методы решения уравнений и
- 4. Задачи курса:Обучить учащихся навыкам решения уравнений и
- 5. В результате изучения элективного курса учащиеся будут
- 6. Они познакомятся с…
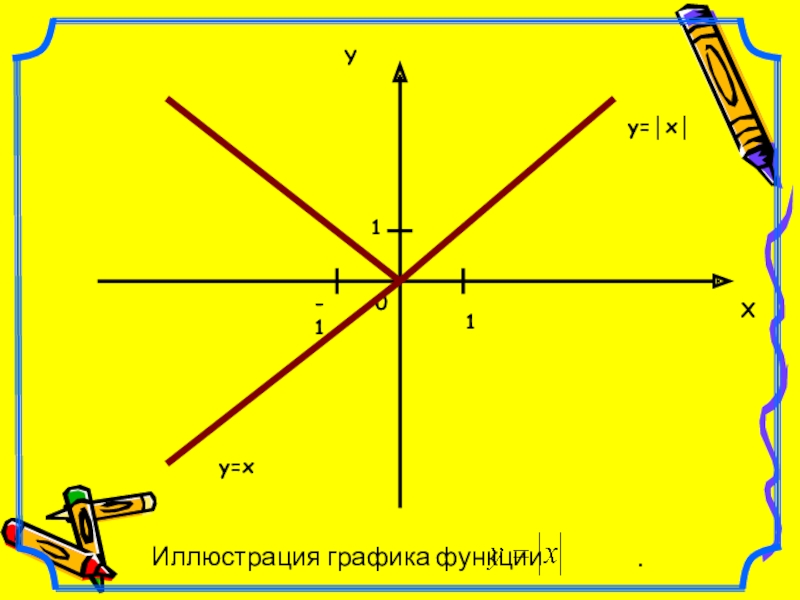
- 7. 0XY11-1y=xy=│x│ Иллюстрация графика функции .
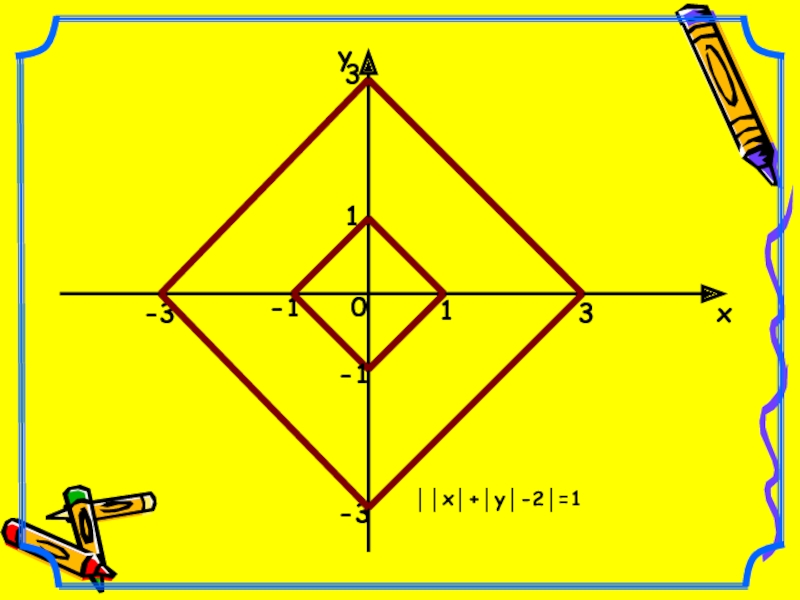
- 8. 0ху1-133-3-3││х│+│у│-2│=11-1
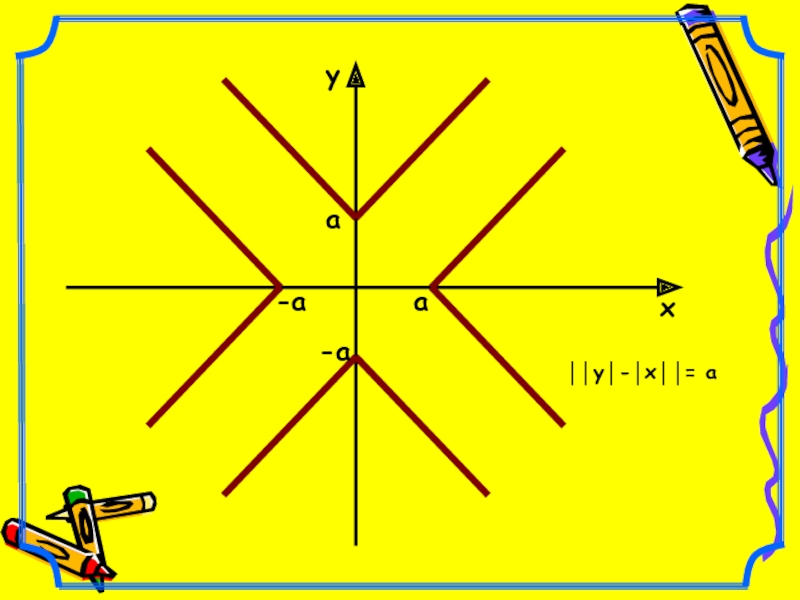
- 9. ухаа-а-а││у│-│х││= а
- 10. Пример №1Решение.Найдем контрольную точку х + 4
- 11. Пример №2 Найдем контрольную точку
- 12. Пример №3Решение: х + 3 = 0
- 13. Они уже изучили…2009-2010
- 14. Они учатся… 2010 – 2011 уч. год
- 15. Подводим итоги…
Программа элективного курса предпрофильной подготовки расчитана НА 17 ЧАСОВ
Слайд 3Цели курса:
рассмотреть методы решения уравнений и неравенств, содержащих модуль;
познакомить учащихся с
основными приемами построения графиков уравнений, содержащих модуль;
привлечь внимание учащихся к эстетической стороне данного вида деятельности.
привлечь внимание учащихся к эстетической стороне данного вида деятельности.
Слайд 4Задачи курса:
Обучить учащихся навыкам решения уравнений и неравенств, содержащих модуль;
Обучить учащихся
навыкам построения и преобразований графиков, содержащих модуль;
Научить учащихся использовать знания, полученные по другим предметам;
Развивать навыки исследовательской работы.
Научить учащихся использовать знания, полученные по другим предметам;
Развивать навыки исследовательской работы.
Слайд 5В результате изучения элективного курса учащиеся будут
знать:
правила раскрытия модуля;
правила построения
основных видов функций с модулем.
уметь:
решать уравнения и неравенства с модулем;
строить графики основных типов функций с модулем и различные их комбинации;
уметь использовать навыки уроков изобразительного искусства и информатики.
уметь:
решать уравнения и неравенства с модулем;
строить графики основных типов функций с модулем и различные их комбинации;
уметь использовать навыки уроков изобразительного искусства и информатики.
Слайд 10Пример №1
Решение.
Найдем контрольную точку х + 4 = 0, х
= - 4.
Рассмотрим промежуток х ‹ - 4.На нем неравенство принимает вид - х – 4 ≥ 1, х ≤ -5. Значит решением является промежуток х ≤ -5.
Рассмотрим промежуток х › - 4.На нем неравенство имеет вид х + 4 ≥ 1, х ≥ - 3.Значит решением является промежуток х ≥ - 3.
Учитывая случаи 1) и 2) Окончательно имеем объединение этих промежутков, т.е (-∞; - 5] u [ - 3; +∞)
Ответ: х ≤ -5 и х ≥ -з. или (-∞; - 5] u [ - 3; +∞)
Рассмотрим промежуток х ‹ - 4.На нем неравенство принимает вид - х – 4 ≥ 1, х ≤ -5. Значит решением является промежуток х ≤ -5.
Рассмотрим промежуток х › - 4.На нем неравенство имеет вид х + 4 ≥ 1, х ≥ - 3.Значит решением является промежуток х ≥ - 3.
Учитывая случаи 1) и 2) Окончательно имеем объединение этих промежутков, т.е (-∞; - 5] u [ - 3; +∞)
Ответ: х ≤ -5 и х ≥ -з. или (-∞; - 5] u [ - 3; +∞)
Слайд 11Пример №2
Найдем контрольную точку х – 3 =
0, х = 3.
Рассмотрим промежуток х ‹ 3. Неравенство имеет вид
- х + 3 ‹ 1, х › 2. Следовательно решением неравенства является промежуток (2; 3).
Рассмотрим промежуток х ≥ 3. Неравенство имеет вид
х – 3 ‹ 1, х ‹ 4.Следовательно решением неравенства является промежуток [ 3; 4).
Рассмотрим вместе эти промежутки. Решением неравенства будет промежуток (2; 4)
Ответ: (2; 4)
Рассмотрим промежуток х ‹ 3. Неравенство имеет вид
- х + 3 ‹ 1, х › 2. Следовательно решением неравенства является промежуток (2; 3).
Рассмотрим промежуток х ≥ 3. Неравенство имеет вид
х – 3 ‹ 1, х ‹ 4.Следовательно решением неравенства является промежуток [ 3; 4).
Рассмотрим вместе эти промежутки. Решением неравенства будет промежуток (2; 4)
Ответ: (2; 4)
Слайд 12Пример №3
Решение: х + 3 = 0
х = -3
При х ‹ -3 получаем уравнение –(х + 3) = 2х – 1
-х – 3 = 2х – 1, -3х = 2, х = - . Но данное число не входит в рассматриваемый промежуток.
При х › -3 получаем х + 3 = 2х – 1, х = 4.
Найденное число входит в рассматриваемый промежуток. Ответ: 4.
При х ‹ -3 получаем уравнение –(х + 3) = 2х – 1
-х – 3 = 2х – 1, -3х = 2, х = - . Но данное число не входит в рассматриваемый промежуток.
При х › -3 получаем х + 3 = 2х – 1, х = 4.
Найденное число входит в рассматриваемый промежуток. Ответ: 4.
-3