- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект по математике логические задачи для учащихся 9-11классов
Содержание
- 1. Проект по математике логические задачи для учащихся 9-11классов
- 2. Слайд 2
- 3. Цель исследования: практически апробировать и проанализировать влияние решения логических задач на развитие интереса на уроках математики.
- 4. Гипотеза проекта: Мы предполагаем, что используя
- 5. Слайд 5
- 6. В чем заключается экспериментВ начале использовать на
- 7. Из истории логических задач: Логика -наука
- 8. Логические задачи отличаются от обычных задач тем,
- 9. Мы решали логические задачи из разделов:
- 10. Приступим к решению
- 11. ЗемлекопыПять землекопов за 5 часов выкапывают 5
- 12. Слайд 12
- 13. Слайд 13
- 14. Приготовление краскиДля того чтобы получить краску оранжевого
- 15. Новые табличкиВ одном городе построили новый район
- 16. 2. Задачи, решаемые с применением кругов Эйлера.
- 17. Задача 1. В группе из 100 туристов
- 18. Решение задачи 1: знают только английский 66-33=33
- 19. Решение задачи 2:Немецкий и французский изучают: 6+3+1+3=10чел. Ответ: 10человек13
- 20. Задача 3. В классе 38 учеников. Из
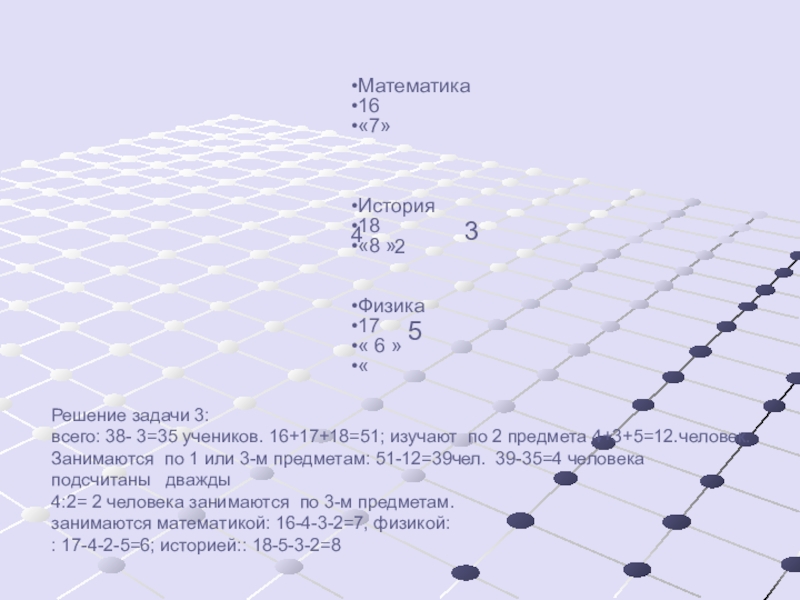
- 21. Решение задачи 3: всего: 38- 3=35
- 22. Задача 4. В некоторой школе есть класс
- 23. 3. Принцип Дирихле Утверждение
- 24. Метод от противного: «Предположим, что не найдется
- 25. Пример 1. В классе 30 человек. Паша
- 26. Пример 2. Имеется 25 конфет 3 сортов.
- 27. Пример 3. В квадратном ковре со стороной
- 28. 4.Задачи на установление числовых закономерностей
- 29. Слайд 29
- 30. Решение: первый треугольник: 6х7+3=42+3=45, второй треугольник:
- 31. Решение:198+198+198+8=602; В=9. ответ:ДРешение : буква а-3; к-5;
- 32. 5.Задачи,решаемые методом исключения(при помощью таблицы истинности)
- 33. 1.В семье трое детей: 2 мальчика и
- 34. 2.Четыре брата Юра, Петя, Вова, Коля учатся
- 35. 3.Три поросенка построили три домика из соломы,
- 36. 4.На улице, став в кружок, беседуют четыре
- 37. 5. Ваня, Петя, Саша и
- 38. 6. Четыре ученицы: Мария, Нина, Ольга и
- 39. Слайд 39
- 40. Ответы:1.Имя девочки начинается с буквы В2.Вова –
- 41. Слайд 41
- 42. 6.Маленькие хитрости: Применение логики при ориентации на видение ответа
- 43. 1. Средняя линия трапеции равна 7 см.
- 44. 2. Две трубы вместе наполняют бассейн за
- 45. 3. Найдите три числа, из которых второе
- 46. 4. Боковые ребра правильной треугольной пирамиды взаимно
- 47. Правильный ответ: Д)Гипотенуза AC равна
- 48. Слайд 48
- 49. Использованная литература:1,Байиф Ж.-К. Логические задачи: Перевод
- 50. Спасибо за внимание
Слайд 1
Учебно-исследовательский проект
на тему: «Логические задачи »
Исследователи: ЖАМАЛЕЕВА АЙНУР,
ЛОПУХИНА
Руководитель проекта:
ГАЛИЦКАЯ НАДЕЖДА ВИКТОРОВНА
КГУ «БЕЛОВСКАЯ СШ МАМЛЮТСКОГО РАЙОНА СЕВЕРО-КАЗАХСТАНСКОЙ ОБЛАСТИ»
Слайд 2 Цель проекта :
* Повысить
математике;
*Формирование и развитие различных видов памяти, внимания.
Слайд 3Цель исследования: практически апробировать и проанализировать влияние решения логических задач на
Слайд 4 Гипотеза проекта:
Мы предполагаем, что используя логическое мышление , как
для поступления в ВУЗ
Слайд 5 Задачи исследования:
Сделать отбор логических
по некоторым разделам;
Провести апробацию способов решения логических задач на уроках математики;
Оценить уровень усвоения программного материала по предмету.
Оценить уровень развития умений применять полученные знания в практической деятельности;
Оценить уровень сформированности логического мышления, интуиции учащихся.
Качественно подготовиться к сдачи ЕНТ
Слайд 6В чем заключается эксперимент
В начале использовать на уроках математики систему подобранных
1)анкета для учащихся «Какие затруднения вы испытываете при решение логических задач по разным учебным предметам?»
2)анкета «Почему ты любишь решать логические задачи?»
3)анкета «Почему ты не любишь решать логические задачи?»
4) анкета «Как повлияло решение логических задач по математике на изучение других предметов?»
Данные методики расположены в той последовательности , к которой они вводятся для определения уровня формирования познавательных интересов учащихся по решению логических задач.
Слайд 7Из истории логических задач:
Логика -наука о формах и законах
Логика была возрождена в середине XIX века.
Слайд 8
Логические задачи отличаются от обычных задач тем, что в них требуется
Слайд 9 Мы решали логические
задачи из разделов:
1.Задачи на количественные соотношения
2. Задачи, решаемые с применением кругов Эйлера
3.Задачи на Принцип Дирихле
4.Задачи на установление числовых закономерностей
5.Задачи,решаемые методом исключения
6.Маленькие хитрости: Применение логики при ориентации
на видение ответа
Слайд 11Землекопы
Пять землекопов за 5 часов выкапывают 5 м канавы. Сколько потребуется
Решение:
Понадобятся те же пять землекопов, не больше. В самом деле, пять землекопов за 5 часов выкапывают 5 м канавы; значит, пять землекопов за 1 час вырыли бы 1 м канавы, а в 100 часов — 100 м.
Слайд 14Приготовление краски
Для того чтобы получить краску оранжевого цвета, необходимо смешать краски
Решение :
Из условия задачи видно, что желтой краски требуется в 3 раза больше, чем красной. Следовательно, имея в наличии 3 грамма желтой краски, необходимо взять 1 грамм красной краски. То есть оранжевой краски при смешивании получиться 4 грамма.
Слайд 15
Новые таблички
В одном городе построили новый район из 100 домов. Мастера
Правильный ответ - 20 девяток.
Слайд 17
Задача 1. В группе из 100 туристов 66 человек знают английский
Задача 2. Из 20 человек двое изучали только английский язык, трое - только немецкий, шестеро — только французский. Никто не изучал трех языков. Один изучал английский и немецкий, трое — английский и французский. Сколько человек изучало немецкий и французский языки?
Слайд 18Решение задачи 1: знают только английский 66-33=33 чел, только французский :54-33=21чел,всего
100
«33»
Слайд 20Задача 3.
В классе 38 учеников. Из них 16 увлекаются математикой
Сколько ребят увлекаются лишь одним из этих предметов?
Слайд 21Решение задачи 3: всего: 38- 3=35 учеников. 16+17+18=51; изучают по 2
4
3
5
2
Слайд 22
Задача 4. В некоторой школе есть класс увлеченных ребят. Семь учеников
Слайд 233. Принцип Дирихле
Утверждение «среди любых трех целых
утверждение «среди 13 человек найдутся двое, родившиеся в один месяц»верно?
Классическая формулировка звучит так: «Если (n + 1) кроликов сидят в n ящиках, то найдётся ящик, в котором сидит, по крайней мере, два кролика».
Слайд 24Метод от противного:
«Предположим, что не найдется двух таких человек. Тогда
Такие утверждения называют
« Принципом Дирихле».
Слайд 25
Пример 1. В классе 30 человек. Паша сделал 13 ошибок, а
Решение: По условию задачи, наибольшее число ошибок, сделанных в работе 13. Значит, ученики могли сделать 0, 1, 2, ..., 13 ошибок. Эти варианты будут «клетками», а ученики станут «кроликами». Тогда по (обобщенному) принципу Дирихле (14 клеток и 30 зайцев)
30:14=2( ост 2)
найдутся три ученика, попавших в одну «клетку», то есть сделавших одинаковое число ошибок
Слайд 26Пример 2. Имеется 25 конфет 3 сортов. Верно ли, что не
Решение:
Пусть «клетками» у нас будут сорта конфет, а «кроликами» -сами конфеты. По принципу Дирихле найдется «клетка», в которой не менее 25 / 3 «кроликов». Так как 8 < 25 / 3 < 9, то найдется 9 конфет одного сорта. Утверждение можно доказать, проводя сразу рассуждения от противного.
Пусть конфет каждого сорта не более 9, то есть не превышает восьми. Тогда всего конфет не больше 3 × 8 = 24, а по условию их 25. Противоречие.
Слайд 27
Пример 3. В квадратном ковре со стороной 1 м моль проела
Решение: Весь ковер можно накрыть такими 25-ю заплатами. По принципу Дирихле Весь ковер можно накрыть такими 25-ю заплатами. По принципу Дирихле какая-то из этих заплат накроет не менее трех дырок. Иногда принцип Дирихле не работает «впрямую»,
Слайд 29
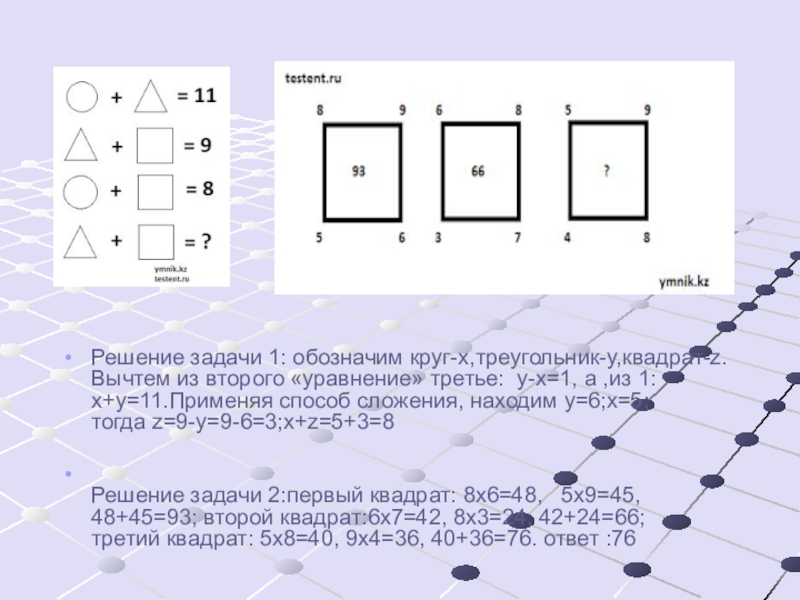
Решение задачи 1: обозначим круг-х,треугольник-у,квадрат-z.Вычтем из второго «уравнение» третье: у-х=1, а
Решение задачи 2:первый квадрат: 8х6=48, 5х9=45, 48+45=93; второй квадрат:6х7=42, 8х3=24, 42+24=66; третий квадрат: 5х8=40, 9х4=36, 40+36=76. ответ :76
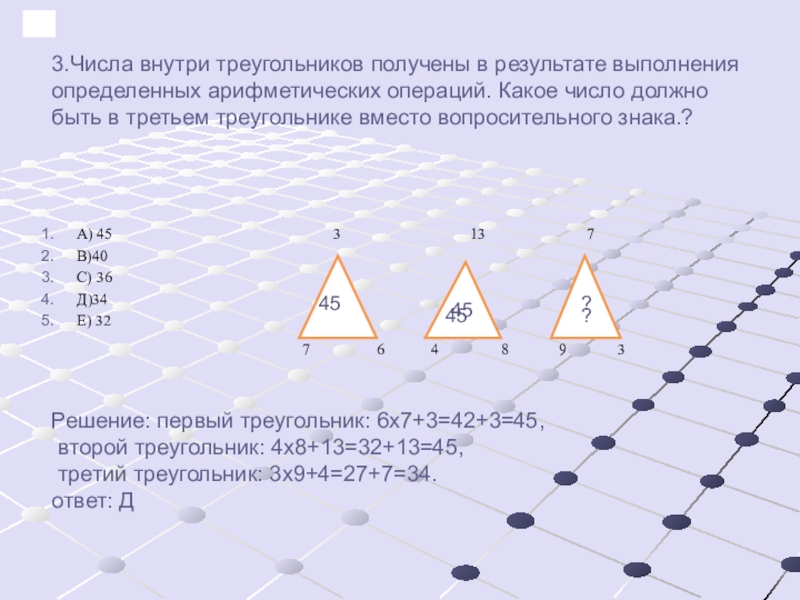
Слайд 30Решение: первый треугольник: 6х7+3=42+3=45, второй треугольник: 4х8+13=32+13=45, третий треугольник: 3х9+4=27+7=34. ответ:
3.Числа внутри треугольников получены в результате выполнения определенных арифметических операций. Какое число должно быть в третьем треугольнике вместо вопросительного знака.?
45
45
?
45
?
Слайд 31Решение:198+198+198+8=602; В=9. ответ:Д
Решение : буква а-3; к-5; ж-4;
р-7; о-1; б-6;
«жоба»-4163
Ответ: Е
4.Подставьте
5. В словах «кара», «жара», «жоба»,
«кора», «кожа»каждой букве соответ
ствует определенная цифра.
Найдите цифровое обозначение
слову «жоба».
А) 5373
В)4373
С)5173
Д)5143
Е)4163
Слайд 33
1.В семье трое детей: 2 мальчика и девочка. Их имена начинаются
Слайд 34
2.Четыре брата Юра, Петя, Вова, Коля учатся в 1,2,3,4 классах. Петя-
Слайд 353.Три поросенка построили три домика из соломы, из прутьев, из камней.
Слайд 36
4.На улице, став в кружок, беседуют четыре девочки – Аня, Валя,
Слайд 37 5. Ваня, Петя, Саша и Коля носят фамилии, начинающиеся
Ваня и С. – отличники,
Петя и В. – троечники,
В. ростом выше П.,
Коля ростом ниже П.,
Саша и Петя имеют одинаковый рост.
На какую букву начинается фамилия каждого мальчика?
Слайд 38
6. Четыре ученицы: Мария, Нина, Ольга и Полина – участвовали в
заняли четыре первых места. На вопрос, кто какое место занял. Они дали три разных ответа:
- Ольга заняла первое место, Нина – второе.
- Ольга – второе, Поля- третье.
- Мария- второе, Поля- четвёртое.
Отвечавшие при этом признали, что одна часть каждого ответа верна, а другая - неверна. Какое место заняла каждая из учениц?
Слайд 40
Ответы:
1.Имя девочки начинается с буквы В
2.Вова – 4кл, Петя – 3кл,
.
3.Наф-наф из камней, Ниф-Ниф из соломы, Нуф- Нуф из прутьев
4.Аня в белом, Валя в голубом, Галя в зеленом, Надя в розовом
5.Ваня П., Петя К., Саша В., Коля С.
6.Оля -1, Мария -2, Поля – 3, Нина -4
7. Учитель предварительно договорился с учениками, чтобы они вызывались отвечать независимо от того, знают ответ или не знают. Но те, кто знает ответ, должны поднимать правую руку, а те, кто не знает, — левую. Учитель каждый раз выбирал другого ученика, но всегда того, кто поднимал правую руку.
Слайд 43
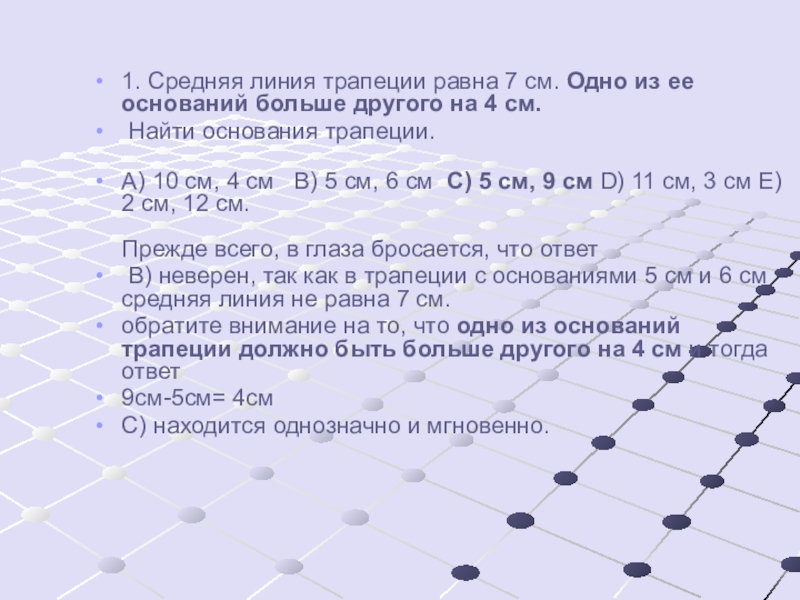
1. Средняя линия трапеции равна 7 см. Одно из ее оснований
Найти основания трапеции.
А) 10 см, 4 см В) 5 см, 6 см C) 5 см, 9 см D) 11 см, 3 см Е) 2 см, 12 см. Прежде всего, в глаза бросается, что ответ
В) неверен, так как в трапеции с основаниями 5 см и 6 см средняя линия не равна 7 см.
обратите внимание на то, что одно из оснований трапеции должно быть больше другого на 4 см и тогда ответ
9см-5см= 4см
С) находится однозначно и мгновенно.
Слайд 44
2. Две трубы вместе наполняют бассейн за 6 часов. Определите, за
А) 10 ч, 20 ч В) 15 ч, 10 ч C) 30 ч, 15 ч D) 25 ч, 20 ч Е) 18 ч, 23 ч.
Если время, необходимое для работы медленного насоса, увеличить на его половину, то получим время работы более производительного насоса.
Такому условию удовлетворяет только ответ В)
(т.е. 15:10=1,5)
Слайд 45
3. Найдите три числа, из которых второе больше первого настолько насколько
А) 8,5; 9; 12
В) 9,1; 3; 4
C) 5; 7; 9
D) 8,5; 10; 11,5
Е) 12; 11; 10.
Решение : Удобнее всего в этом задании вычислить произведения двух меньших чисел в каждом из приведенных ответов.
Это произведение будет равно 85 только в ответе D).
Ответ D) удовлетворяет также остальным двум условиям задания.
Слайд 46
4. Боковые ребра правильной треугольной пирамиды взаимно перпендикулярны и равны по
A) 9,6 В)5,4 C) 4,5 D) 4,9 E) 4,8
Задача сложна только на первый взгляд, так как возникает проблема нахождения высоты пирамиды.
Решение : «поставим» ее на одну из боковых граней, и решение на много облегчено: основанием является прямоугольный треугольник, высотой – одно из боковых ребер.
V=1/3*S*H=1/3*(1/2*3*3*)*3=4,5см
Ответ С).
Слайд 47Правильный ответ:
Д)Гипотенуза AC равна
радиусу окружности
5.Прямоугольный треугольник вписан в четверть
А)Площадь треугольника ABC равна площади сегмента BCE
В)Площадь треугольникаABC вдвое меньше площади сегмента BCE
С)Периметр прямоугольника ABCD равен 20
Д)Гипотенуза AC равна радиусу окружности
Е)Катет BC больше катета AB в 2 раза
Слайд 48
Логические задачи - это своеобразная «гимнастика для ума».Решение логических задач развивает мышление и воображение и это помогает творчески мыслить в разных ситуациях и творчески подходить к поставленным целям. Мы попробовали разобраться в некоторых видах задач, научились применять различные методы и подходы к их решению. Стали мудрее и будем применять логику при изучении других предметов.
Слайд 49Использованная литература:
1,Байиф Ж.-К. Логические задачи: Перевод с франц./ Перевод Сударева
2,Клименченко Д.В. Задачи по математике для любознательных: Книга для учащихся 5-6кл. средней школы - М. Просвещения, 1992.- 192с
.
3,Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Книга для учащихся старших классов 3 издание: Просвещение - 1989г.
4, Информация из интернета: PoteheChas.ru – Ваш интеллектуальный досуг.
5. Материалы сайтов:
https://infourok.ru/logicheskie_zadachi_po_ent-536217.htm
https://vk.com/logiconline
https://urokimatematiki.ru/sbornik-logicheskie-zadachi-ent-5037.html
http://ymnik.kz/tests/mathematical-literacy/
https://kopilkaurokov.ru/matematika/testi/podghotovka-k-ient-po-matiematikie-loghichieskiie-zadachi