- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект по алгебре Арифметическая и геометрическая прогрессии (9 класс)
Содержание
- 1. Проект по алгебре Арифметическая и геометрическая прогрессии (9 класс)
- 2. АктуальностьТемы «Арифметическая прогрессия» и «Геометрическая прогрессия» очень
- 3. Цель и задачиЦель: обобщить и систематизировать знания
- 4. История возникновения Задачи на арифметические и
- 5. Сведения, связанные с прогрессиями, впервые
- 6. Слайд 6
- 7. Исторические задачи «Пусть тебе сказано: раздели
- 8. Карл Гаусс считается одним из величайших математиков
- 9. Задача - легендаИндийский царь Шерам позвал к
- 10. Решение задачи - легендыДано:
- 11. Слайд 11
- 12. Формула для вычисления разности арифметической прогрессии
- 13. Задача
- 14. bn= b1. qn-1
- 15. = bn-1. bn+1
- 16. 1Sn=b1.n, q=1
- 17. Слайд 17
- 18. Подготовка к ГИА
- 19. Слайд 19
- 20. Слайд 20
- 21. Задача 4:Найдите сумму первых трех членов геометрической
- 22. Задача 5:Три положительных числа
- 23. +
- 24. Задачи для самостоятельного решения:Задача 1:Найдите наиболее близкий
- 25. Задача 1:Найдите наиболее близкий к нулю отрицательный
- 26. 2:
- 27. Задача 3:Найдите сумму бесконечно убывающей геометрической прогрессии
- 28. Слайд 28
- 29. Задача 4:Является ли число 64 членом геометрической
- 30. Интересные фактыХимия. При повышении температуры по арифметической
- 31. Литература и интернет-ресурсыУчебник Алгебра. 9 класс :
АктуальностьТемы «Арифметическая прогрессия» и «Геометрическая прогрессия» очень важные в курсе 9 класса. Они актуальны, так как задание по данным темам встречаются на ГИА и ЕГЭ, не достаточно высокий уровень решения задач данного типа учащимися 9-х и
Слайд 1Арифметическая и геометрическая прогрессия
Выполнили:
Ученицы 9 «А» класса
Котюсова Елена и Макарова Ксения.
Слайд 2Актуальность
Темы «Арифметическая прогрессия» и «Геометрическая прогрессия» очень важные в курсе 9
класса. Они актуальны, так как задание по данным темам встречаются на ГИА и ЕГЭ, не достаточно высокий уровень решения задач данного типа учащимися 9-х и 11-х классов.
Слайд 3Цель и задачи
Цель:
обобщить и систематизировать знания по теме: «Прогрессии».
Задачи:
повторить
темы «Арифметическая прогрессия» и «Геометрическая прогрессия» в сравнении;
история возникновения прогрессий;
подбор задач для подготовки к ГИА и их решение.
история возникновения прогрессий;
подбор задач для подготовки к ГИА и их решение.
Слайд 4История возникновения
Задачи на арифметические и геометрические прогрессии встречаются у
вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах». Но на связь между прогрессиями впервые обратил внимание Архимед.
Слайд 5
Сведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах
Древней Греции. Уже в V в. до н.э. греки знали следующие прогрессии и их суммы:
1+2+3+…+n =
2+4+6+…+2n = n(n+1)
Слайд 7Исторические задачи
«Пусть тебе сказано: раздели 10 мер ячменя между
10 людьми, разность же между каждым человеком и его соседом равна меры».
Формула, которой пользовались египтяне:
Формула, которой пользовались египтяне:
Задача из древнеегипетского папируса Ахмеса:
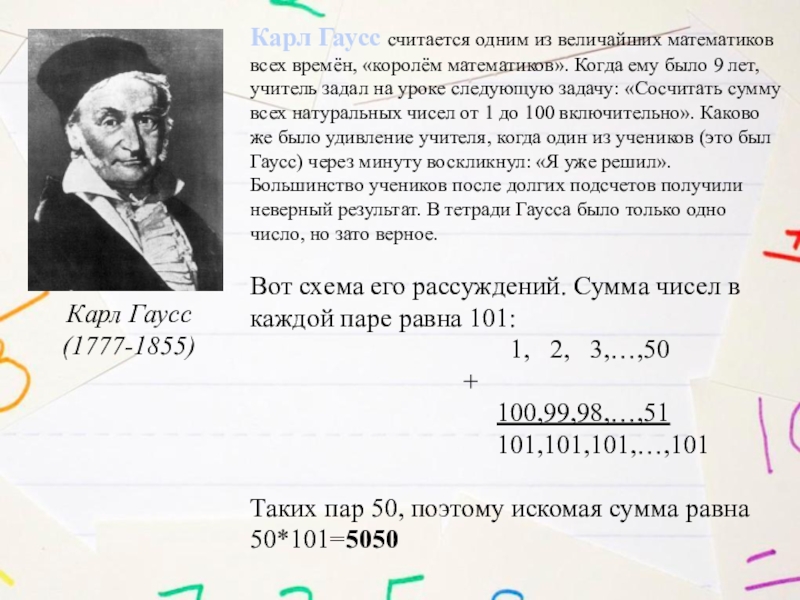
Слайд 8Карл Гаусс считается одним из величайших математиков всех времён, «королём математиков».
Когда ему было 9 лет, учитель задал на уроке следующую задачу: «Сосчитать сумму всех натуральных чисел от 1 до 100 включительно». Каково же было удивление учителя, когда один из учеников (это был Гаусс) через минуту воскликнул: «Я уже решил». Большинство учеников после долгих подсчетов получили неверный результат. В тетради Гаусса было только одно число, но зато верное.
Вот схема его рассуждений. Сумма чисел в каждой паре равна 101:
1, 2, 3,…,50 + 100,99,98,…,51 101,101,101,…,101
Таких пар 50, поэтому искомая сумма равна 50*101=5050
Вот схема его рассуждений. Сумма чисел в каждой паре равна 101:
1, 2, 3,…,50 + 100,99,98,…,51 101,101,101,…,101
Таких пар 50, поэтому искомая сумма равна 50*101=5050
Карл Гаусс
(1777-1855)
Слайд 9Задача - легенда
Индийский царь Шерам позвал к себе изобретателя шахматной игры,
своего подданого Сету, чтобы наградить его за остроумную выдумку. Сета потребовал за первую клетку шахматной доски 1 зерно, за вторую – 2 зерна, за третью – 4 зерно и т.д. Обрадовавшийся царь посмеялся над Сетой и приказал выдать ему такую «скромную» награду. Стоит ли царю смеяться?
Слайд 10Решение задачи - легенды
Дано: - геом. прогрессия; 1,
2, 4, 8, 16,…
=1, g=2, n=64
Найти:
Решение:
=1, g=2, n=64
Найти:
Решение:
S = 18 446 744 073 709 551 615
Слайд 21Задача 4:
Найдите сумму первых трех членов геометрической прогрессии, в которой
= -18, = 486.
Решение:
1) 2)
3) =
Ответ: = -14.
Решение:
1) 2)
3) =
Ответ: = -14.
bn= b1.qn-1
S3
Слайд 22Задача 5:
Три положительных числа , ,
образуют геометрическую прогрессию. Их сумма равна 21, а сумма обратных им величин равна . Найдите ; 0, 0, 0.
Решение:
=
+ + = 21 + + = 21 q
+ + = + + =
Решение:
=
+ + = 21 + + = 21 q
+ + = + + =
Слайд 23 +
+ = 21 = 21
+ + 1 = = = 36
( 1 + + ) = 21 =
+ + 1 = 0 ( по усл.)
( ) = 21 = 6
= 21 :
Ответ: = 6.
+ + 1 = = = 36
( 1 + + ) = 21 =
+ + 1 = 0 ( по усл.)
( ) = 21 = 6
= 21 :
Ответ: = 6.
Слайд 24Задачи для самостоятельного решения:
Задача 1:
Найдите наиболее близкий к нулю отрицательный член
арифметической прогрессии 49,5 ; 47,7 ; …
Задача 2:
Найдите сумму всех натуральных чисел, не превосходящих 200, которые делятся на 8.
Задача 3:
Найдите сумму бесконечно убывающей геометрической прогрессии , если + = и + = 20.
Задача 4:
Является ли число 64 членом геометрической прогрессии 3;1;…?
Задача 2:
Найдите сумму всех натуральных чисел, не превосходящих 200, которые делятся на 8.
Задача 3:
Найдите сумму бесконечно убывающей геометрической прогрессии , если + = и + = 20.
Задача 4:
Является ли число 64 членом геометрической прогрессии 3;1;…?
Слайд 25Задача 1:
Найдите наиболее близкий к нулю отрицательный член арифметической прогрессии 49,5
; 47,7 ; …
Решение:
d = 47,7 – 49,5 = -1,8 2)
Ответ: = 0,9.
Решение:
d = 47,7 – 49,5 = -1,8 2)
Ответ: = 0,9.
Слайд 27Задача 3:
Найдите сумму бесконечно убывающей геометрической прогрессии ,
если + = и + = 20.
Решение:
+ = 20 + = ( 1 + ) = 20 ( 1 + ) = 1 + = ( 1 + ) =
Решение:
+ = 20 + = ( 1 + ) = 20 ( 1 + ) = 1 + = ( 1 + ) =
bn= b1.qn-1
Слайд 29Задача 4:
Является ли число 64 членом геометрической прогрессии 3;1;…?
Решение:
1)
64 = 0,5
= 64 : 0,5
= 128
т.к. n = 8
Ответ: да, является.
= 64 : 0,5
= 128
т.к. n = 8
Ответ: да, является.
bn=b1.qn-1
.
Слайд 30Интересные факты
Химия. При повышении температуры по арифметической прогрессии, скорость химических реакций
растет по геометрической прогрессии.
Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.
Физика. Нейтрон, ударяя по ядру урана, раскалывает его на 2 части. Затем 2 нейтрона, ударяя по двум ядрам, раскалывают их еще на 4 части и т.д. – это геометрическая прогрессия.
Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, их число удваивается.
Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.
Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.
Физика. Нейтрон, ударяя по ядру урана, раскалывает его на 2 части. Затем 2 нейтрона, ударяя по двум ядрам, раскалывают их еще на 4 части и т.д. – это геометрическая прогрессия.
Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, их число удваивается.
Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.
Слайд 31Литература и интернет-ресурсы
Учебник Алгебра. 9 класс : учебник для общеобразовательных учреждений
/ А45 [ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова] ; под ред. С.А. Теляковского. – 17-е изд. – М. : Просвещение, 2010.
Математика. 9 класс. Подготовка к ГИА – 2013 : учебно-методическое пособие / под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону : Лешон, 2012.
Алгебра : сборник заданий для подготовки к государственной итоговой аттестации в 9 классе / [ Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович и др.] – М. : Просвещение, 2011.
www.grandars.ru
www.wikipedia.org
Математика. 9 класс. Подготовка к ГИА – 2013 : учебно-методическое пособие / под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону : Лешон, 2012.
Алгебра : сборник заданий для подготовки к государственной итоговой аттестации в 9 классе / [ Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович и др.] – М. : Просвещение, 2011.
www.grandars.ru
www.wikipedia.org