В.А.,
ученица 10 класса
Руководитель:
Букреева Т. А.,
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект Математические кривые вокруг нас
Содержание
- 1. Проект Математические кривые вокруг нас
- 2. Цель работыПознакомить с некоторыми математическими кривыми, которые встречаются и имеют практическое применение в нашей жизни.
- 3. ПараболаГрафиком функции f(x)=ax2+bx+c (a≠0) является парабола.
- 4. Парабола в техникеПараболическую антенну можно увидеть около
- 5. Парабола в космосеНекоторые космические тела, такие как
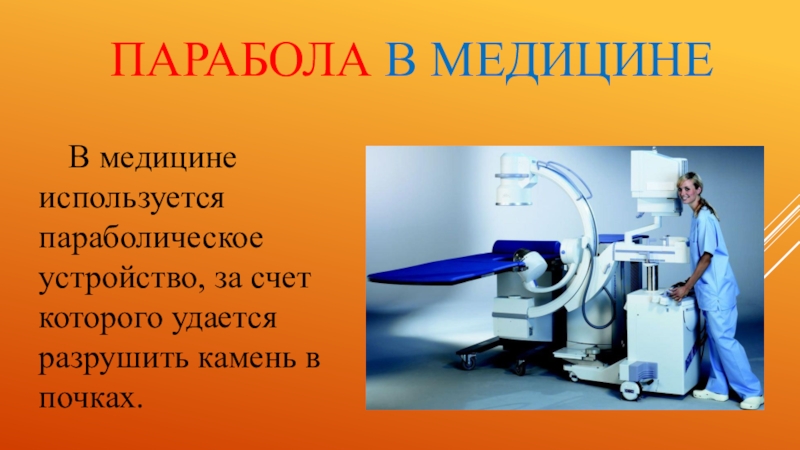
- 6. Парабола в медицинеВ медицине используется параболическое устройство, за счет которого удается разрушить камень в почках.
- 7. Парабола в архитектуреАрхитектурные свойства арки в форме
- 8. Парабола в архитектуреЖивописный мост в МосквеОкеанографический парк на открытом воздухе в Валенсии, Испания
- 9. Парабола в архитектуреЗолотые ворота — один из
- 10. Парабола в архитектуреСтадион Фишт в г. Сочи.
- 11. Парабола в дизайне одежды (Клинья юбки)
- 12. Парабола в природеМорская пещера в Алгарве, Португалия.
- 13. Парабола в природе
- 14. Гипербола
- 15. Гипербола и дорогиНи шоссейная, ни железная дороги
- 16. гипербола в архитектуреФорма гиперболы используется в архитектуре при строительстве мостов, различных интересных сооружений (например, американские горки).
- 17. гипербола в архитектуреЭйфелева башня в Париже.
- 18. Гипербола в архитектуреСимвол Рейкьявика — собор Хатльгримскиркья,
- 19. Гипербола в дизайне одежды
- 20. Гипербола в природе
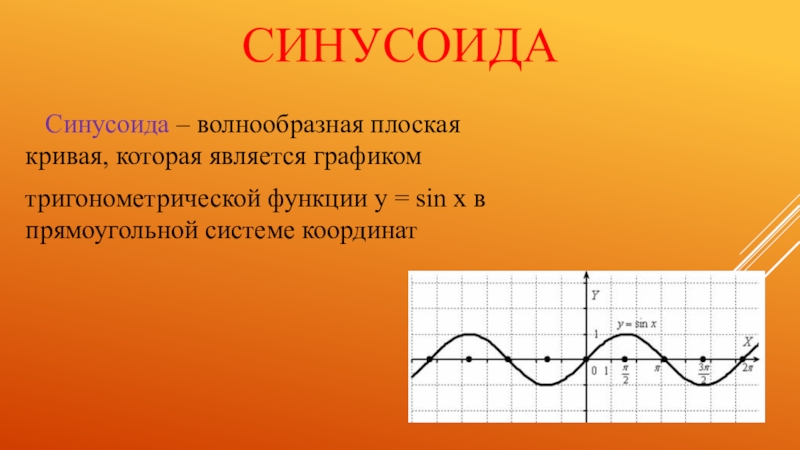
- 21. Синусоида Синусоида – волнообразная плоская кривая,
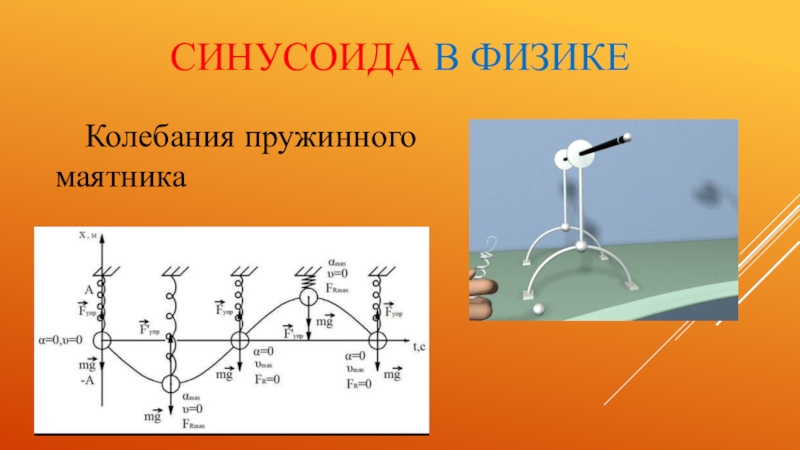
- 22. Синусоида в физикеКолебания пружинного маятника
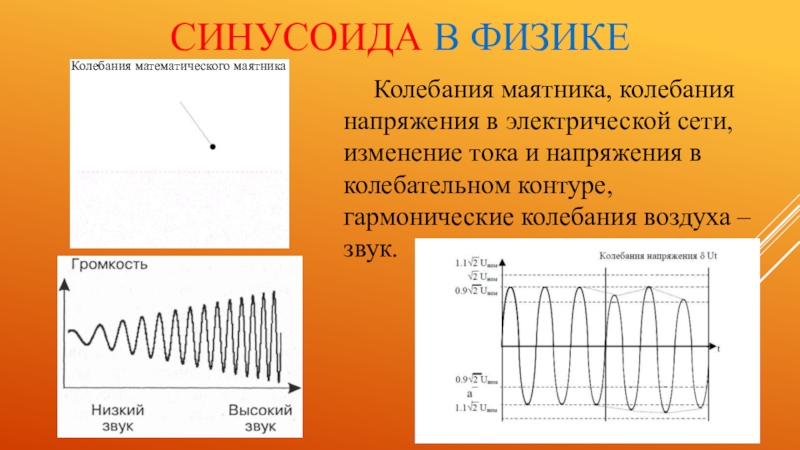
- 23. Синусоида в физикеКолебания математического маятникаКолебания маятника, колебания
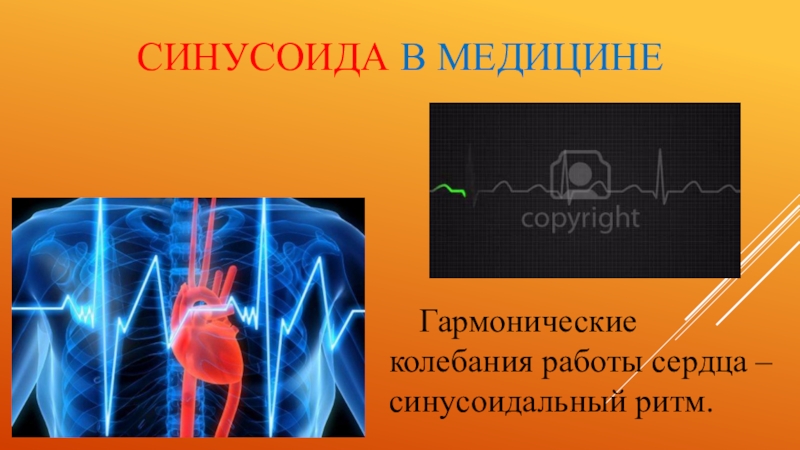
- 24. Синусоида в медицинеГармонические колебания работы сердца – синусоидальный ритм.
- 25. Синусоида в архитектуреМузей и выставочный центр Пауля Клее в Берне, ШвейцарияВинодельня Bodegas Ysios, Испания
- 26. Синусоида в дизайне одежды (Жабо)
- 27. Синусоида в природе
- 28. Эллипс Эллипс — замкнутая кривая на
- 29. Эллипс в астрономииСогласно закону, открытому в начале
- 30. Эллипс в архитектуреЗдание планетария в Копенгагене, носящего
- 31. Эллипс в архитектуреРимский Колизей, грандиозный античный амфитеатр,
- 32. Эллипс в архитектуре«Зелёная» вилла, ЯпонияCybertecture Egg (здание-яйцо) в Мумбае
- 33. Эллипс в бытуВ форме эллипса можно изготовить
- 34. Эллипс в дизайнеДизайнеры выбирают эллиптическую форму для цветников, фонтанов и искусственных водоёмов, для предметов интерьера.
- 35. Эллипс в дизайне одежды (овальный силуэт)
- 36. Эллипс в природеЛистья растений, множество фруктов, овощей,
- 37. Спираль АрхимедаСпираль Архимеда - это плоская кривая,
- 38. Спираль Архимеда в техникеПо спирали Архимеда идёт
- 39. Спираль Архимеда в техникеОдна из деталей швейной
- 40. Спираль Архимеда в техникеСамым распространенным техническим устройством
- 41. Спираль Архимеда в техникеВинт Архимеда стал прообразом
- 42. Логарифмическая спиральЛогарифмическая спираль – это плоская кривая,
- 43. Спираль в техникеВ теории механизмов логарифмическая спираль
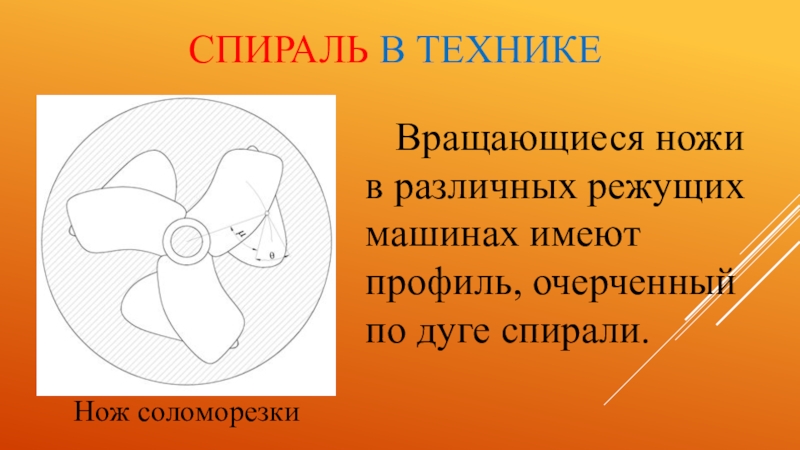
- 44. Спираль в техникеВращающиеся ножи в различных режущих машинах имеют профиль, очерченный по дуге спирали. Нож соломорезки
- 45. Спирали в архитектуреСпиралевидная лестница на выходе из музея в Ватикане
- 46. Спирали в архитектуреПеревернутая башня масонов в Синтре, Португалия
- 47. Спирали в космосеПо спиралям закручены многие галактики, в частности Галактика, которой принадлежит Солнечная система.
- 48. Спирали в природеВодоворотТорнадо
- 49. Спирали в природеРаковины многих моллюсков, улиток, рога
- 50. Спирали в природеОдин из наиболее распространенных пауков
- 51. Спирали в природеГоловка подсолнуха состоит из спиралей,
- 52. Спирали в природеСосновые шишки и колючки кактусов
- 53. Спирали в природеСпирали алоэ и ананаса
- 54. Спирали в дизайне одежды (Воланы)
- 55. Циклоида Циклоидой называют кривую, которую описывает точка окружности, катящейся без скольжения по неподвижной прямой.
- 56. Циклоида в архитектуреХудожественный музей Кимбелла, штат Техас, СШАБиблиотека Святой Женевьевы, Франция
- 57. Циклоида в дизайне одежды (Фестона)
- 58. ЗаключениеВ данной работе я наглядно показала, что
- 59. Источники1. А. И. Маркушевич «Замечательные кривые»; Москва;
Цель работыПознакомить с некоторыми математическими кривыми, которые встречаются и имеют практическое применение в нашей жизни.
Слайд 2Цель работы
Познакомить с некоторыми математическими кривыми, которые встречаются и имеют практическое
применение в нашей жизни.
Слайд 3Парабола
Графиком функции f(x)=ax2+bx+c (a≠0) является парабола.
Параболой называется геометрическое место точек, равноудалённых от данной точки и от данной прямой.
Слайд 4Парабола в технике
Параболическую антенну можно увидеть около любого аэродрома. Используется для
того, чтобы собрать в одну точку сигналы радиолокатора, отраженные от самолета.
Слайд 5Парабола в космосе
Некоторые космические тела, такие как кометы или астероиды, проходящие
вблизи крупных космических объектов на высокой скорости, имеют траекторию движения в форме параболы.
Слайд 6Парабола в медицине
В медицине используется параболическое устройство, за счет которого удается
разрушить камень в почках.
Слайд 7Парабола в архитектуре
Архитектурные свойства арки в форме параболы делают ее идеальной
математически. Перевернутая цепная линия – это арка, которая держит сама себя и не требует никаких дополнительных опор. Ворота Сент-Луиса в Миссури – прекрасный пример такой арки.
Слайд 8Парабола в архитектуре
Живописный мост в Москве
Океанографический парк на открытом воздухе в
Валенсии, Испания
Слайд 9Парабола в архитектуре
Золотые ворота — один из немногих памятников оборонного зодчества
Киевской Руси периода правления Ярослава Мудрого
Слайд 10Парабола в архитектуре
Стадион Фишт в г. Сочи. На нем было открытие
и закрытие Олимпиады 2014 г..
Слайд 15Гипербола и дороги
Ни шоссейная, ни железная дороги никогда не заворачивают круто,
а переходят всегда с одного направления на другое плавно, без переломов, дугой. Кривая, отвечающая за нашу безопасность на автомобильных и железных дорогах (траектория закругления дорог) – гипербола.
Слайд 16гипербола в архитектуре
Форма гиперболы используется в архитектуре при строительстве мостов, различных
интересных сооружений (например, американские горки).
Слайд 18Гипербола в архитектуре
Символ Рейкьявика — собор Хатльгримскиркья, лютеранская церковь. Это здание
занимает четвертое место по высоте среди всех зданий Исландии.
Слайд 21Синусоида
Синусоида – волнообразная плоская кривая, которая является графиком
тригонометрической
функции y = sin x в прямоугольной системе координат
Слайд 23Синусоида в физике
Колебания математического маятника
Колебания маятника, колебания напряжения в электрической сети,
изменение тока и напряжения в колебательном контуре, гармонические колебания воздуха – звук.
Слайд 25Синусоида в архитектуре
Музей и выставочный центр Пауля Клее в Берне, Швейцария
Винодельня
Bodegas Ysios, Испания
Слайд 28Эллипс
Эллипс — замкнутая кривая на плоскости, которая может быть
получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.
Слайд 29Эллипс в астрономии
Согласно закону, открытому в начале XVII в. немецким астрономом
Иоганном Кеплером, все планеты движутся вокруг Солнца по орбитам, имеющим форму эллипса.
Слайд 30Эллипс в архитектуре
Здание планетария в Копенгагене, носящего имя Тихо Браге —
знаменитого датского астронома, учителя Иоганна Кеплера. Здание в форме усечённого цилиндра имеет крышу эллиптической формы.
Слайд 31Эллипс в архитектуре
Римский Колизей, грандиозный античный амфитеатр, вмещавший до 70 000
зрителей. Его арена, на которой устраивались состязания и зрелища, также ограничена эллипсом.
Слайд 33Эллипс в быту
В форме эллипса можно изготовить журнальный столик, раму для
картины, декоративное блюдо, циферблат часов, зеркало, посуду, раковину или соткать ковер.
Слайд 34Эллипс в дизайне
Дизайнеры выбирают эллиптическую форму для цветников, фонтанов и искусственных
водоёмов, для предметов интерьера.
Слайд 36Эллипс в природе
Листья растений, множество фруктов, овощей, орехов также имеют форму
эллипса. И это только малая часть примеров, когда мы в своей окружающей жизни можем увидеть эллипс.
Слайд 37Спираль Архимеда
Спираль Архимеда - это плоская кривая, которую вырисовывает точка, движущаяся
с постоянной скоростью от центра окружности по ее радиусу, окружность которого вращается также с постоянной угловой скоростью.
Слайд 38Спираль Архимеда в технике
По спирали Архимеда идёт на грампластинке звуковая дорожка.
Перемещение острия корундовой иглы по этой дорожке будет результирующим двух равномерных движений: приближения к полюсу и вращение вокруг полюса.
Слайд 39Спираль Архимеда в технике
Одна из деталей швейной машины – механизм для
равномерного наматывания ниток на шпульку – имеет форму спирали Архимеда.
Слайд 40Спираль Архимеда в технике
Самым распространенным техническим устройством является винт Архимеда —
механизм, исторически использовавшийся для передачи воды из низколежащих водоёмов в оросительные каналы.
Слайд 41Спираль Архимеда в технике
Винт Архимеда стал прообразом шнека («улитки») - устройства,
широко используемого в различных машинах для перемешивания жидких, сыпучих и тестообразных материалов. Самая распространенная его разновидность - винтовой ротор в обычной мясорубке.
Слайд 42Логарифмическая спираль
Логарифмическая спираль – это плоская кривая, которую вырисовывает точка, движущаяся
не с постоянной (как в случае спирали Архимеда) скоростью, а с возрастающей, причем это возрастание пропорционально расстоянию от центра окружности.
Слайд 43Спираль в технике
В теории механизмов логарифмическая спираль применятся при проектировании зубчатых
колес с переменным передаточным числом.
Слайд 44Спираль в технике
Вращающиеся ножи в различных режущих машинах имеют профиль, очерченный
по дуге спирали.
Нож соломорезки
Слайд 47Спирали в космосе
По спиралям закручены многие галактики, в частности Галактика, которой
принадлежит Солнечная система.
Слайд 49Спирали в природе
Раковины многих моллюсков, улиток, рога таких млекопитающих, как архары
(горные козлы), закручены по логарифмической спирали.
Слайд 50Спирали в природе
Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает
нити вокруг центра по логарифмической спирали.
Слайд 51Спирали в природе
Головка подсолнуха состоит из спиралей, одни из которых закручены
по часовой стрелке, другие - против.
Слайд 52Спирали в природе
Сосновые шишки и колючки кактусов также имеют спирали, направленные
по часовой, или против часовой стрелки.
Слайд 55Циклоида
Циклоидой называют кривую, которую описывает точка окружности, катящейся без скольжения
по неподвижной прямой.
Слайд 56Циклоида в архитектуре
Художественный музей Кимбелла, штат Техас, США
Библиотека Святой Женевьевы, Франция
Слайд 58Заключение
В данной работе я наглядно показала, что окружающий нас мир сложен
и разнообразен. Несмотря на все его разнообразия форм, черт, линий, можно представить, что этот мир состоит из множества кривых. Математические кривые часто встречаются в природе и жизни.
Мы их видим каждый день!
Мы их видим каждый день!
Слайд 59Источники
1. А. И. Маркушевич «Замечательные кривые»; Москва; ―Наука‖ -1978г.
2. Штейнгауз «Математический
калейдоскоп»; Москва; ―ГосТехИздат‖ -1949г.
3. Г. Н. Берман «Циклоида»; Москва; ―ГосТехИздат‖ -1954г.
4. М. Д. Аксенова «Энциклопедия для детей. Математика том11», Москва; Издательский центр «Аванта+», 1998г.
5. Энциклопедический словарь юного математика/Сост. Э-68 А. П. Савин. –М.: Издательство «Педагогика», 1989 г.
6. https://moluch.ru
7. http://ru-wiki.or
8. http://atlanticrus.ru/content
9. https://yandex.ru/images
3. Г. Н. Берман «Циклоида»; Москва; ―ГосТехИздат‖ -1954г.
4. М. Д. Аксенова «Энциклопедия для детей. Математика том11», Москва; Издательский центр «Аванта+», 1998г.
5. Энциклопедический словарь юного математика/Сост. Э-68 А. П. Савин. –М.: Издательство «Педагогика», 1989 г.
6. https://moluch.ru
7. http://ru-wiki.or
8. http://atlanticrus.ru/content
9. https://yandex.ru/images