- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Применение производной в жизни
Содержание
- 1. Применение производной в жизни
- 2. Слайд 2
- 3. В математике следует помнить не формулы, а
- 4. Девиз. В мире не происходит ничего в
- 5. С ее появлением математика перешагнула из
- 6. «Метод флюкций». Так Ньютон назвал свою
- 7. КОНКУРСМодераторов
- 8. Задача № 1. Заряд, протекающий через проводник
- 9. Решение:(q)`= cos*(2t-10)*2= 2*cos*(2t-10)Согласно условиям задачи, t равно
- 10. Слайд 10
- 11. подумайте
- 12. НАШЁЛ ! Нет, не долетит 2м
- 13. молодцы!!!
- 14. З а д а ч а 3.
- 15. Задача 4 4Автомобиль
- 16. подумайте Да, т.к. скорость через 7 сек. будет равна 6 м/с.
- 17. Работа в командах
- 18. Задача ДидоныДидона –дочь тирского царя,легендарная основательница и
- 19. Слайд 19
- 20. Развалины Бирсы в Тунисе
- 21. Легенда об основании Карфагена гласит, что когда
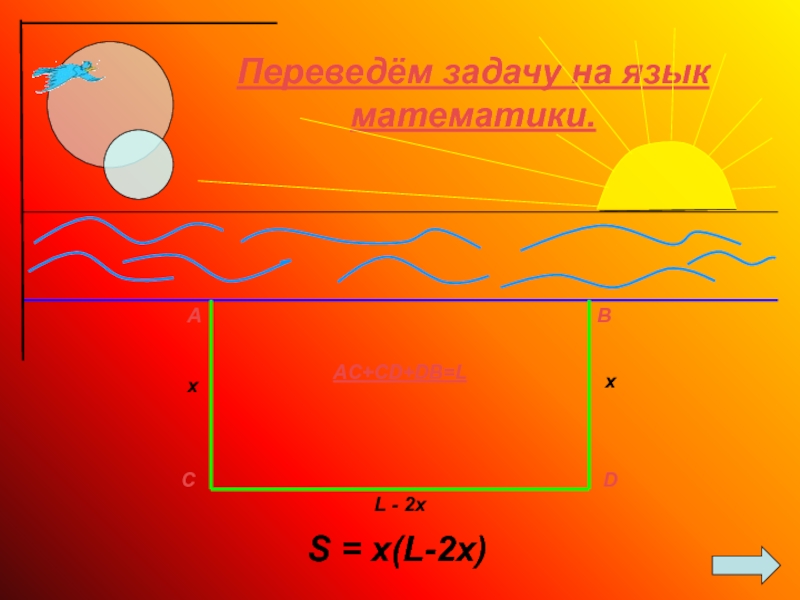
- 22. ABCDAC+CD+DB=LxxL - 2xПереведём задачу на язык математики.S = x(L-2x)
- 23. Y = x(L-2x) → maxY′ = L
- 24. Рассказ «Много ли человеку земли нужно» Л.Н.Толстой
- 25. Мой университет - www.moi-mummi.ru
- 26. Много ли человеку земли надо?PABCD = 40Наибольшей ли площади выбрал участок Пахом?1310152SABCD = ?
- 27. Какой из четырёхугольников имеет наибольшую площадь?Мой университет - www.moi-mummi.ru
- 28. Прямоугольник:P = 40 кмa = x кмb
- 29. 3. Окно имеет форму прямоугольника, периметр которого
- 30. 1.В чём различие задач? 2.Что общего?
- 31. Слайд 31
- 32. Знакомство с понятиями прикладных задач математики.
- 33. Задачи
- 34. Поиск оптимального решенияНаивысшая производительность трудаМой университет - www.moi-mummi.ru
- 35. Поиск оптимального решенияМой университет - www.moi-mummi.ru Наименьшие потери
- 36. Поиск оптимального решенияМой университет - www.moi-mummi.ru Минимальные затраты времени
- 37. Поиск оптимального решенияМой университет - www.moi-mummi.ru Максимальная прибыль
- 38. Схема решения оптимизационных задачПроанализировав условие задачи, определить,
- 39. Задача3: Предприятие производит Х единиц некоторой
- 40. Решение: Функция
- 41. Вывод:Производная функции успешно применяется при решении оптимальных
- 42. Домашнее заданиеПовторить теоретический материал пощади фигурМой университет - www.moi-mummi.ru
- 43. Итоги урока Продолжите
- 44. СПАСИБО ЗА РАБОТУ! УСПЕХОВ ВАМ!
Слайд 1Тема:Применение производной в жизни.
Выполнила учитель математики КГУ «Гимназия №2» города Рудного
Слайд 3В математике следует помнить не формулы, а процессы мышления.
ЕРМАКОВ Василий Петрович
Слайд 4Девиз. В мире не происходит ничего в чем бы ни был виден
Эйлер Леонард (1707—1783), математик, физик, механик, астроном.
Слайд 5 С ее появлением математика перешагнула из алгебры в математический анализ.
2)
3) Бывает первой, второй, … .
Слайд 6
«Метод флюкций». Так Ньютон назвал свою работу,
посвященную основным понятиям
анализа. Функцию Ньютон назвал флюентой,
а производную – флюкцией. Обозначения Ньютона
для производных - х* (с точкой) и у* - сохранились
в физике до сих пор.
Производная – одно из фундаментальных понятий
математики. Оно возникло в XV11 веке. Независимо друг
от друга И.Ньютон и Г.Лейбниц разработали основные
элементы дифференциального исчисления.
Исторические сведения
Исчисление, созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии.
Слайд 8Задача № 1.
Заряд, протекающий через проводник , меняется по закону
q=sin*(2t-10)
Найти силу тока в момент времени t=5 cек.
Слайд 9Решение:
(q)`= cos*(2t-10)*2= 2*cos*(2t-10)
Согласно условиям задачи, t равно 5 секундам , откуда
(q)`= 2*cos*(2*5 – 10) = 2* cos 0 = 2 (А)
Ответ: I = 2 (А).
Слайд 10
Слайд 14З а д а ч а 3. Пусть популяция бактерий в
Слайд 15Задача 4
4Автомобиль приближается к мосту с
Слайд 18Задача Дидоны
Дидона –дочь тирского царя,легендарная основательница и первая царица Карфагена.Она отплыла
Слайд 21
Легенда об основании Карфагена гласит, что когда финикийский корабль пристал к
Вопрос: какую наибольшую площадь земли могли купить финикийцы?
Слайд 23
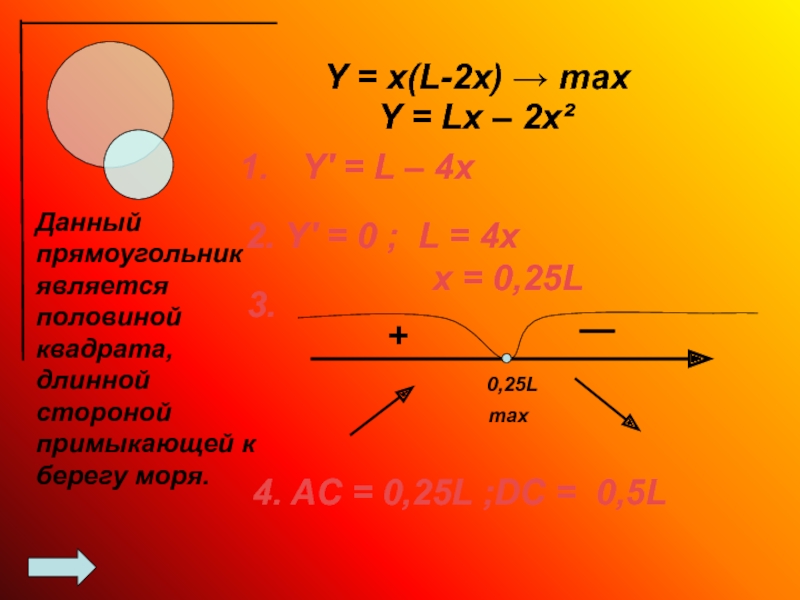
Y = x(L-2x) → max
Y′ = L – 4x
0,25L
+
—
max
Данный прямоугольник является
2. Y′ = 0 ; L = 4x
x = 0,25L
3.
4. AC = 0,25L ;DC = 0,5L
Y = Lx – 2x²
Слайд 24Рассказ «Много ли человеку земли нужно» Л.Н.Толстой
О крестьянине Пахоме, покупавшем
-А цена какая будет?- говорит Пахом.
-Цена у нас одна: 1000 рублей за день.
Не понял Пахом.
-Какая же это мера – день? Сколько в ней десятин будет?
-Мы этого, - говорит, - не умеем считать. А мы за день продаем; сколько обойдешь в день, то и твое, а цена 1000 рублей.
Удивился Пахом.
-Да ведь это, - говорит, -в день обойти земли много будет.
Засмеялся старшина.
-Вся твоя, - говорит. – Только один уговор: если назад не придешь в день к тому месту, с какого возьмешься, пропали твои деньги.
Какой хочешь круг забирай, только до захода солнца приходи к тому месту, с какого взялся. Что обойдешь, все твое.
Слайд 26Много ли человеку земли надо?
PABCD = 40
Наибольшей ли площади выбрал участок
13
10
15
2
SABCD = ?
Слайд 28Прямоугольник:
P = 40 км
a = x км
b = (20-x) км
S =
D(S) = (0;20)
S(x) = 20x – x²
S’(x) = 20 – 2x = -2 (x - 10)
-2*(х-10)=0 х=10
Ответ:
10км, 10км
Слайд 293. Окно имеет форму прямоугольника, периметр которого равен 8 м. Каковы
Слайд 32Знакомство с понятиями прикладных задач математики.
Задачи на нахождение наибольшего и
Слайд 33 Задачи на оптимизацию
II этап. Работа с составленной моделью
III этап. Ответ на вопрос задачи
Слайд 34Поиск оптимального решения
Наивысшая производительность труда
Мой университет - www.moi-mummi.ru
Слайд 38Схема решения оптимизационных задач
Проанализировав условие задачи, определить, наибольшее или наименьшее значение
Принять за независимую переменную одну из неизвестных величин и обозначить её буквой x. Определить её границы изменения.
Задать функцию y=f(x).
Найти средствами математики наибольшее или наименьшее значение на промежутке изменения х.
Интерпретировать результат для рассматриваемой задачи.
Слайд 39Задача3: Предприятие производит Х единиц некоторой
однородной продукции в месяц. Установлено, что
зависимость финансовых накопления предприятия
от объема выпуска выражается формулой
f(x)=-0,02x3 + 600x -1000.
Исследовать потенциал предприятия.
.
Слайд 40 Решение:
Функция исследуется с помощью производной.
Получаем, что при Х=100 функция достигает
максимума.
Вывод:
Финансовые накопления предприятия растут
с увеличением объема производства
до 100 единиц,
при х =100 они достигают максимума и объем
накопления равен 39000 денежных единиц.
Дальнейший рост производства приводит к
сокращению финансовых накоплений.
Слайд 41
Вывод:
Производная функции успешно применяется при решении оптимальных задач в различных сферах
Д/з решить задачу: Рекламный щит имеет форму прямоугольника S = 9 м². Изготовьте щит в виде прямоугольника с наименьшим периметром. Определите его стоимость, если суммарная цена материалов и работ по изготовлению за 1 м² составляет 200 грн + 25 грн за погонный метр длины щита.
Слайд 42Домашнее задание
Повторить теоретический
материал пощади фигур
Мой университет - www.moi-mummi.ru
Слайд 43Итоги урока
Продолжите фразу:
«Сегодня на уроке я
«Сегодня на уроке я научился…»
«Сегодня на уроке я познакомился…»
«Сегодня на уроке я повторил…»
«Сегодня на уроке я закрепил…»
«Сегодня на уроке я совершенствовал…»