- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презинтация по математики на тему Матрицы
Содержание
- 1. Презинтация по математики на тему Матрицы
- 2. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИМатрицей размера m
- 3. Обозначение:гдеi=1,2…mj=1,2…n- матрица размерности m x n- элемент матрицы i –ой строки и j -го столбца,
- 4. матрица размерности m x n
- 5. Две матрицы называются равными, если у них
- 6. Пример:- квадратная матрица размерности 3х3
- 7. Элементы матрицы aij , у которых номер
- 8. единичная матрица
- 9. Нулевой называется матрица, все элементы которой равны нулю.нулевая матрица
- 10. Матрица, состоящая из одной строки, называется матрицей-строкой иливектором-строкой.матрица-строка
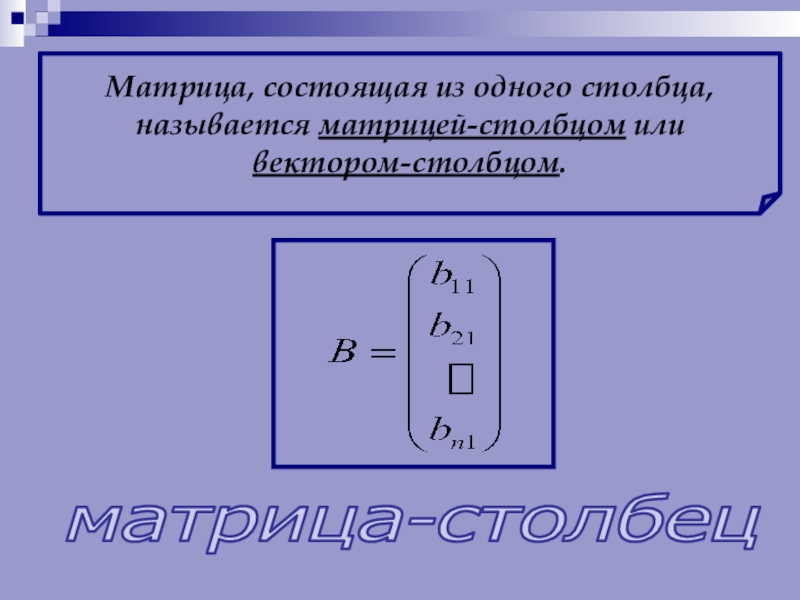
- 11. Матрица, состоящая из одного столбца, называется матрицей-столбцом иливектором-столбцом.матрица-столбец
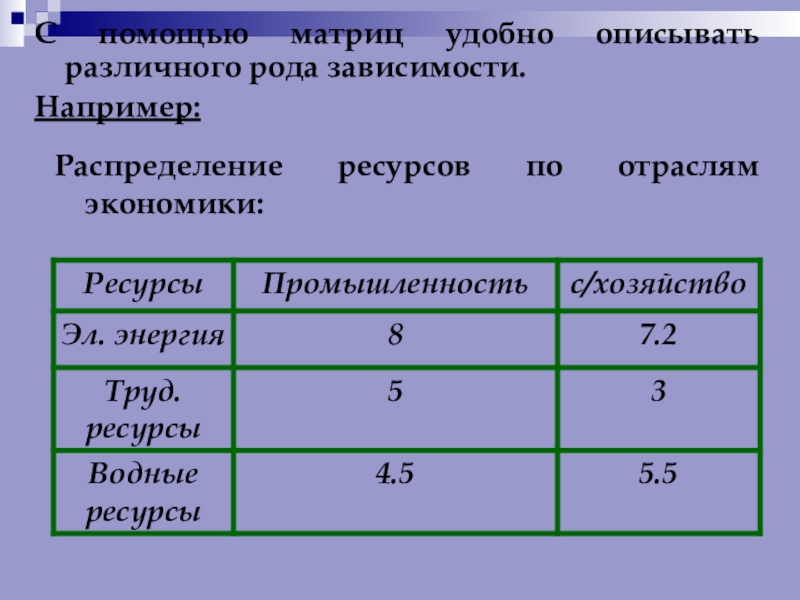
- 12. Распределение ресурсов по отраслям экономики:С помощью матриц удобно описывать различного рода зависимости.Например:
- 13. Эту зависимость можно представить в виде матрицы:Где
- 14. ДЕЙСТВИЯ НАД МАТРИЦАМИ1. Умножение матрицы на числоЧтобы
- 15. Пусть дана матрица Умножаем ее на число λ:Где каждый элемент матрицы В:Где:
- 16. Например:Умножая матрицу на число 2, получим:
- 17. 2. Сложение матрицСкладываются матрицы одинаковой размерности. Получается
- 18. Пусть даны матрицы Складываем их:Где каждый элемент матрицы С:Аналогично проводится вычитание матриц.
- 19. Пример.Найти сумму и разность матриц:
- 20. Решение:
- 21. 3. Умножение матрицУмножение матриц возможно, если число
- 22. Пусть даны матрицы Умножаем их:Где каждый элемент матрицы С:
- 23. Пример.Найти произведение матриц:
- 24. Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует:Решение:
- 25. Теперь перемножим матрицы в обратном порядке:Умножение матриц в общем случае некоммутативно:
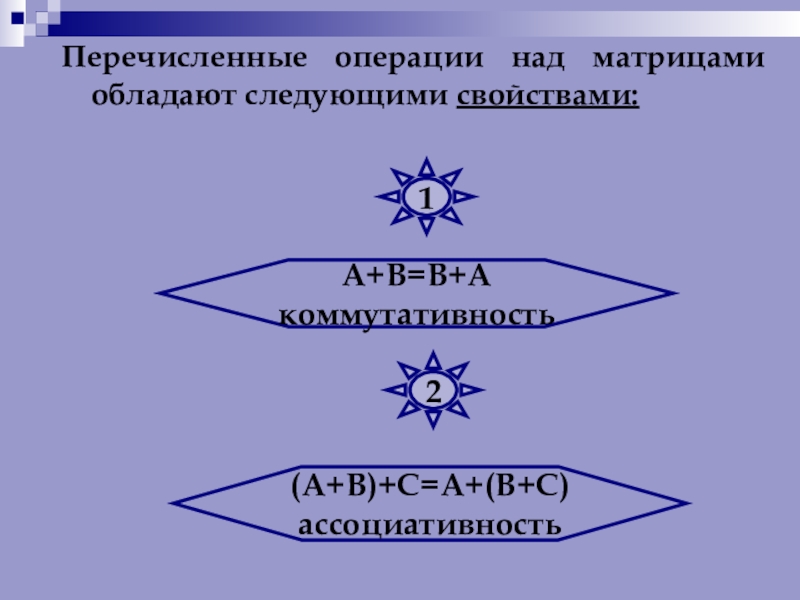
- 26. Перечисленные операции над матрицами обладают следующими свойствами:А+В=В+Акоммутативность(А+В)+С=А+(В+С)ассоциативность12
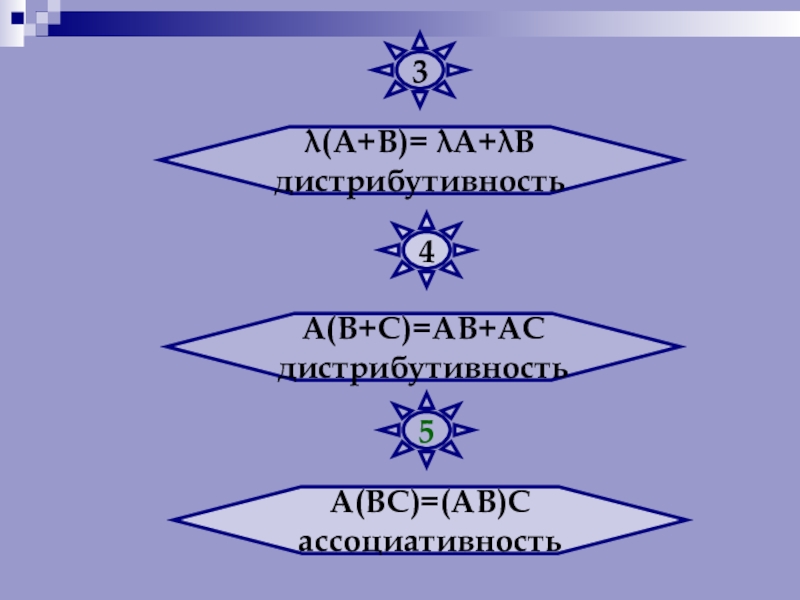
- 27. λ(А+В)= λА+λВдистрибутивностьА(В+С)=АВ+АСдистрибутивностьА(ВС)=(АВ)Сассоциативность345
- 28. 4. Транспонирование матрицМатрица АТ называется транспонированной к
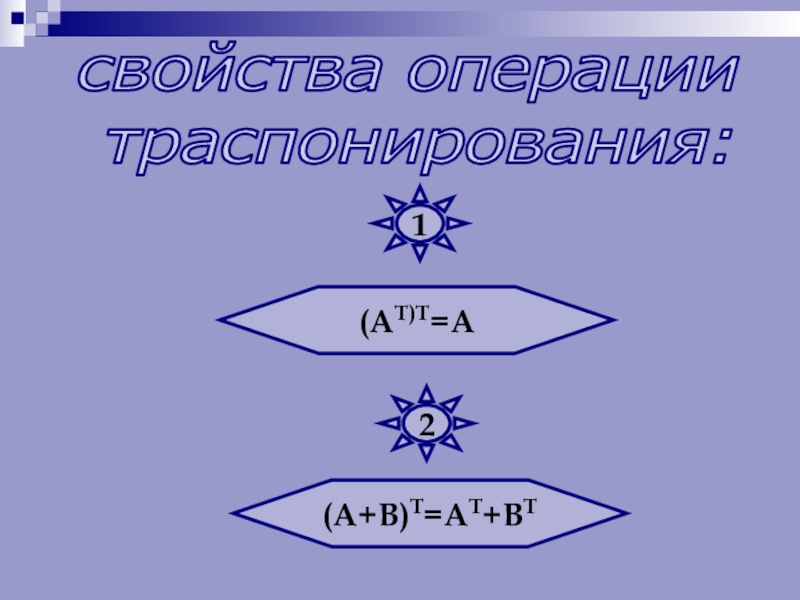
- 29. (АТ)Т=А(А+В)Т=АТ+ВТсвойства операции траспонирования:12
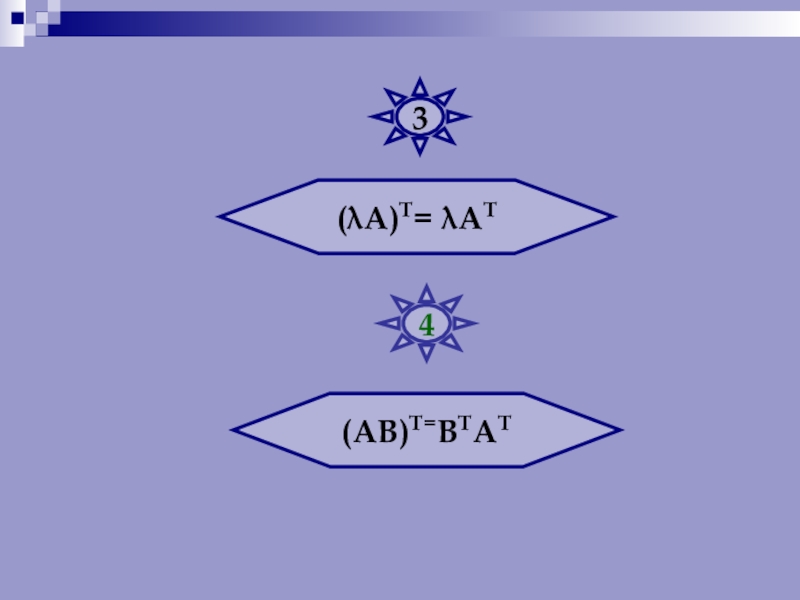
- 30. (λА)Т= λАТ(АВ)Т=ВТАТ34
- 31. Пример.Транспонировать матрицу:
- 32. Решение:
МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИМатрицей размера m x n называетсяпрямоугольная таблица чисел, содержащая m строк и n столбцов.Числа, составляющие матрицу, называются элементами матрицы.
Слайд 2МАТРИЦЫ И ДЕЙСТВИЯ
НАД НИМИ
Матрицей размера m x n называется
прямоугольная таблица
чисел,
содержащая m строк и n столбцов.
содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются элементами матрицы.
Слайд 3Обозначение:
где
i=1,2…m
j=1,2…n
- матрица размерности m x n
- элемент матрицы i –ой строки
и j -го столбца,
Слайд 5Две матрицы называются равными, если
у них одинаковая размерность и
совпадают
строки и столбцы.
Квадратной матрицей n-го порядка
называется матрица размера n на n.
Слайд 7Элементы матрицы aij , у которых номер
столбца совпадает с номером
строки,
называются диагональными.
называются диагональными.
Единичной (обозначается Е) называется
диагональная матрица с единицами на
главной диагонали.
Слайд 10Матрица, состоящая из одной строки,
называется матрицей-строкой или
вектором-строкой.
матрица-строка
Слайд 11Матрица, состоящая из одного столбца,
называется матрицей-столбцом или
вектором-столбцом.
матрица-столбец
Слайд 12Распределение ресурсов по отраслям экономики:
С помощью матриц удобно описывать различного рода
зависимости.
Например:
Например:
Слайд 13Эту зависимость можно представить в виде матрицы:
Где элемент aij показывает сколько
i – го ресурса потребляет j – отрасль.
Например, a32 показывает, сколько воды потребляет сельское хозяйство.
Например, a32 показывает, сколько воды потребляет сельское хозяйство.
Слайд 14ДЕЙСТВИЯ НАД МАТРИЦАМИ
1. Умножение матрицы на число
Чтобы умножить матрицу на число,
надо
каждый элемент матрицы умножить на
это число.
каждый элемент матрицы умножить на
это число.
Полученные произведения образуют итоговую матрицу.
Слайд 172. Сложение матриц
Складываются матрицы одинаковой
размерности. Получается матрица той же
размерности,
каждый элемент которой
равен сумме соответствующих
элементов исходных матриц.
равен сумме соответствующих
элементов исходных матриц.
Слайд 18Пусть даны матрицы
Складываем их:
Где каждый элемент матрицы С:
Аналогично проводится вычитание
матриц.
Слайд 213. Умножение матриц
Умножение матриц возможно, если число столбцов первой матрицы равно
числу строк второй.
Тогда каждый элемент полученной матрицы равен сумме произведений элементов i – ой строки первой матрицы на соответствующие элементы j-го столбца второй.
Тогда каждый элемент полученной матрицы равен сумме произведений элементов i – ой строки первой матрицы на соответствующие элементы j-го столбца второй.
Слайд 24Число столбцов первой матрицы равно числу строк второй, следовательно их произведение
существует:
Решение:
Слайд 25Теперь перемножим матрицы в обратном порядке:
Умножение матриц в общем случае некоммутативно:
Слайд 26Перечисленные операции над матрицами обладают следующими свойствами:
А+В=В+А
коммутативность
(А+В)+С=А+(В+С)
ассоциативность
1
2
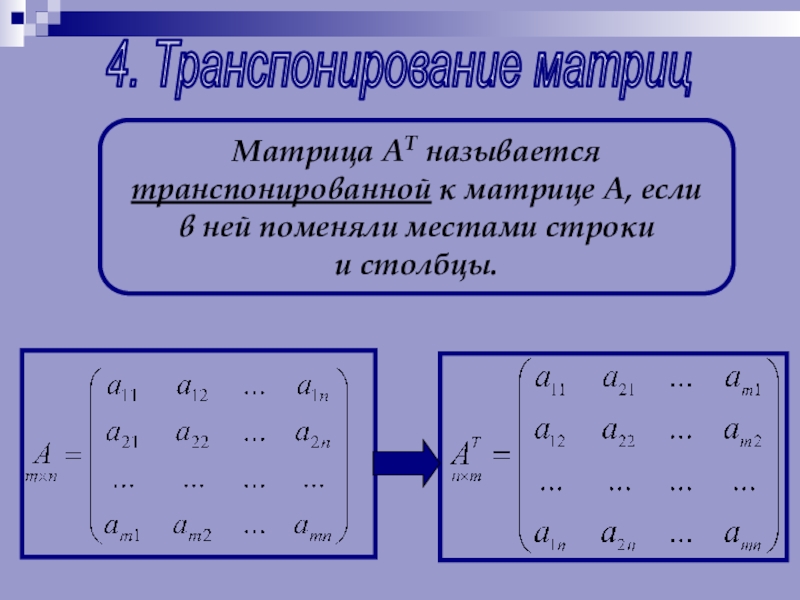
Слайд 284. Транспонирование матриц
Матрица АТ называется
транспонированной к матрице А, если
в
ней поменяли местами строки
и столбцы.
и столбцы.
