- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентація Розв`язування завдань з модулями
Содержание
- 1. Презентація Розв`язування завдань з модулями
- 2. .
- 3. Для
- 4. Розв'язування рівнянь з модулями методом интервалів
- 5. №2
- 6. Розв'язування нерівностей з модулями| х |
- 7. Наприклад:|х-6| х +5 > 2
- 8. Нераівності виду │f1 (x)│+…│fm (x)│- │fm+1(x)│-…-│fn(x)│>g(x)№3Нулі
- 9. Слайд 9
- 10. Для побудови графіка функції у = |f(х)
- 11. Для побудови графіка функції у = f
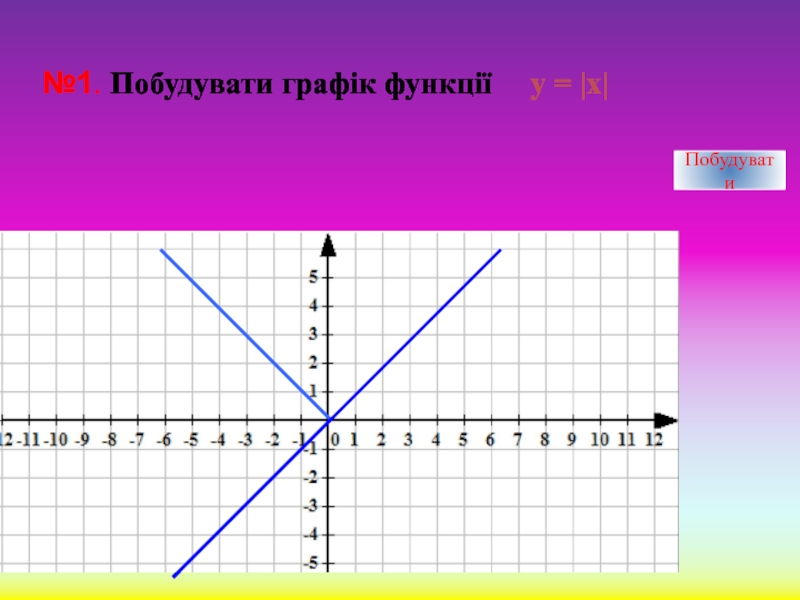
- 12. №1. Побудувати графік функції у = |х|Побудувати
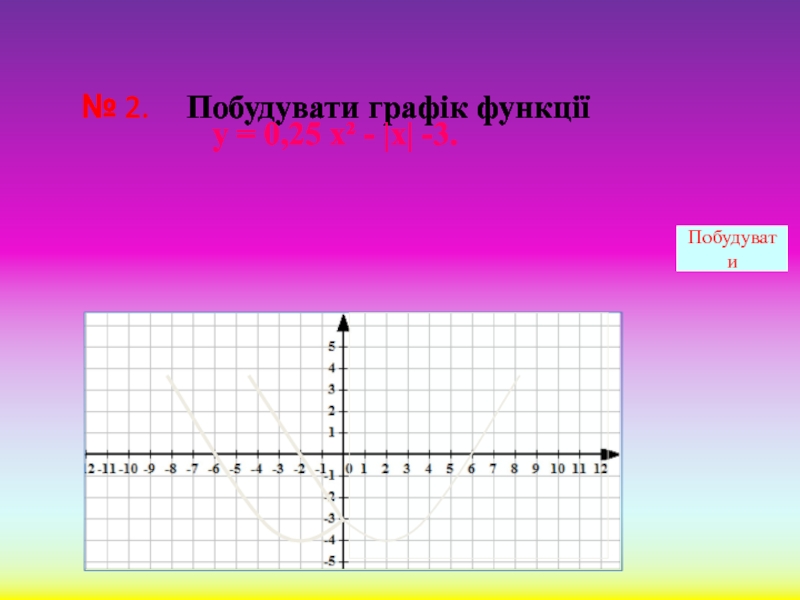
- 13. № 2. Побудувати графік функції у = 0,25 х² - |х| -3. Побудувати
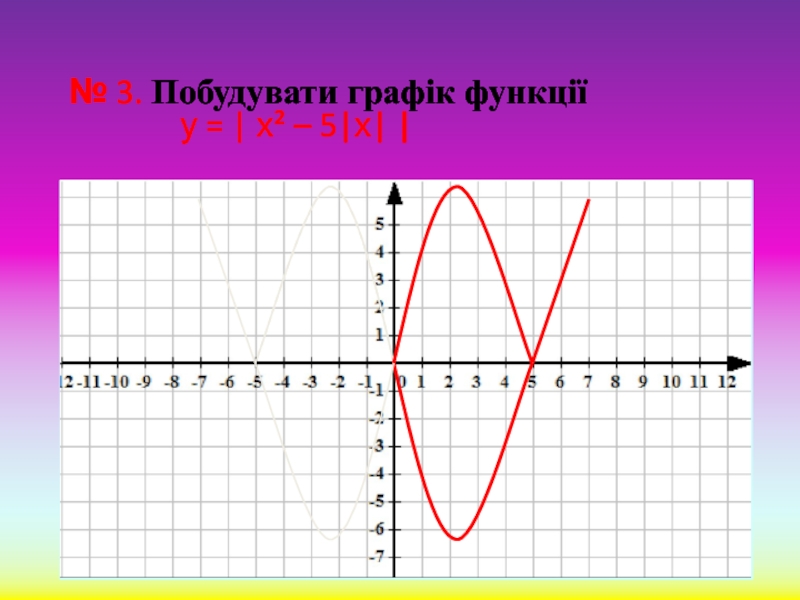
- 14. № 3. Побудувати графік
- 15. Побудова графіків функції виду у =│f1 (x)│+…│fm
- 16. Завдання для самостійного розв'язання: Розв'язати рівняння:1)
Слайд 3
Для того, щоб розв‘язати рівняння,
1. знайти значення змінних, при яких вирази, що знаходяться під знаком модуля, обертаються в нуль (знайти нулі модулів);
2. розбити область допустимих значень рівняння на проміжки на кажному з яких вирази, що стоять під модулем, зберігають знак ;
3. на кожному з таких проміжків рівняння записують без знака модуля, а потім розв‘язують його.
Об‘єднання розв'язків, знайдених на всіх проміжках, і є розв'язком даного рівняння.
Розв'язування рівнянь з модулями
методом интервалів
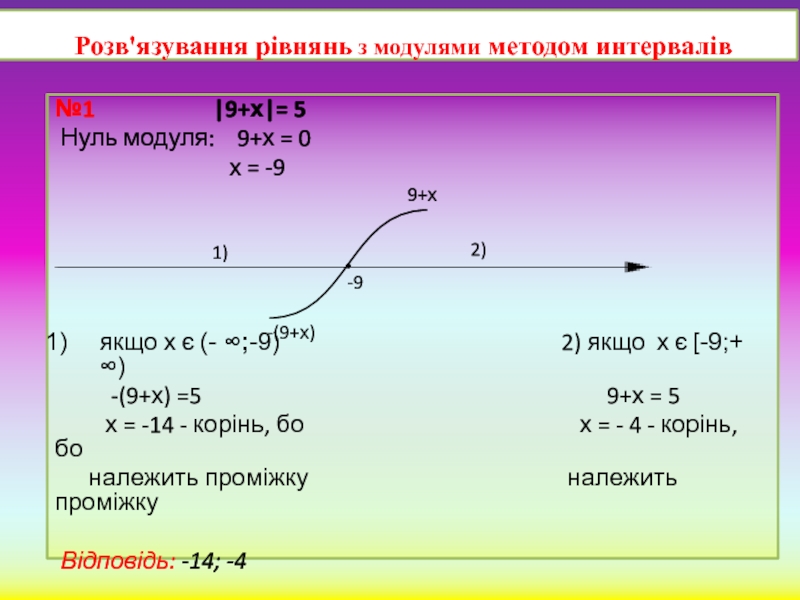
Слайд 4 Розв'язування рівнянь з модулями методом интервалів
№1
Нуль модуля: 9+х = 0
х = -9
якщо х є (- ∞;-9) 2) якщо х є [-9;+ ∞)
-(9+х) =5 9+х = 5
х = -14 - корінь, бо х = - 4 - корінь, бо
належить проміжку належить проміжку
Відповідь: -14; -4
-9
1)
2)
-(9+х)
9+х
Слайд 5№2
Нулі модулів: х+4 = 0 х-6 = 0
х = -4 х = 6
-4
6
-(х-6)
х-6
х+4
-(х+4)
1)
2)
3)
Нулі модулів розбивають промінь на проміжки, на яких всі підмодульні вирази мають постійний знак. Розкриваємо модулі і розв'язуємо рівняння на кожному з трьох утворених проміжків. Корені рівнянь повинні належати даним проміжкам.
якщо х є (- ∞;-4] 2) якщо х є (-4; 6)
-(х-6)-(х+4) = 7 х+4-(х-6) = 7
-2х+2 = 7 х+4-х+6 = 7
-2х = 5 0х+10 = 7
х = -2,5 – стор. корінь 0х = -3
3) якщо х є [ 6;+ ∞) (ǿ)
х+4+х-6 = 7
2х-2 = 7
х = 4,5 – стор. корінь Відповідь: рівняння коренів не має
Слайд 6Розв'язування нерівностей з модулями
| х | ≤ a
| х
Розв'язання:
Розв'язання:
-a
-a
a
a
x
x
-a ≤ х ≤ a
х ≤ -a ;
x ≥ a
x ͼ [ -a; a ]
x ͼ (- ∞; -a ] U [a; + ∞)
-a ≥ х ≥ a
х ≤ a
х ≥ -a
Слайд 7Наприклад:
|х-6|
1 11
x ͼ [ 1; 11 ]
2. |х+5| > 2
Розв'язання:
-2 > х +5 > 2
- 7 > х > - 3
- 7 - 3
x ͼ (- ∞; -7 ] U [-3; + ∞)
x
x
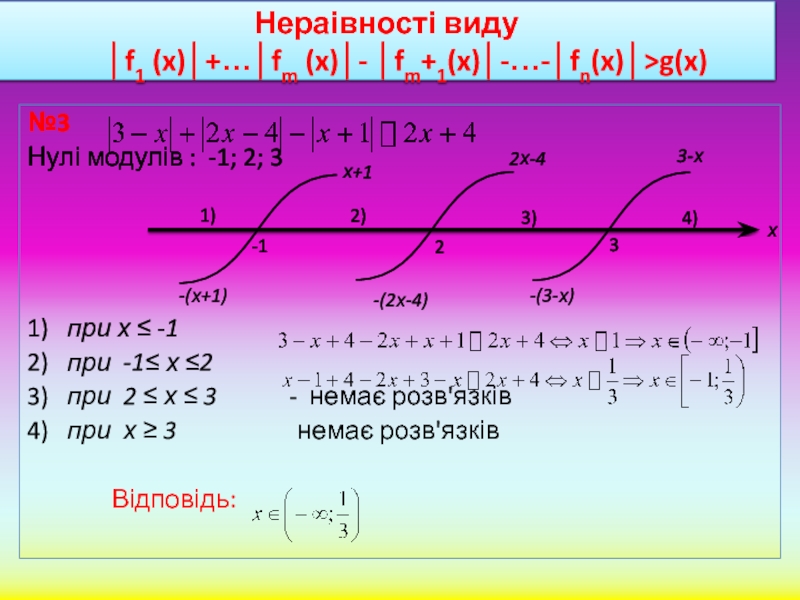
Слайд 8Нераівності виду
│f1 (x)│+…│fm (x)│- │fm+1(x)│-…-│fn(x)│>g(x)
№3
Нулі модулів : -1; 2; 3
1) при х ≤ -1
2) при -1≤ х ≤2
3) при 2 ≤ х ≤ 3 - немає розв'язків
4) при х ≥ 3 немає розв'язків
Відповідь:
-1
2
3
х
х+1
-(х+1)
-(2х-4)
-(3-х)
2х-4
3-х
1)
2)
3)
4)
:
Слайд 9 Побудова графіків
y=f(|x|), y=|f(x)|, y=|f|x||
Методичні рекомендації:
Коли у «стандартні» функції, які задають прямі, параболи, гіперболи, включають знак модуля, їхні графіки становляться незвичайними. Щоб навчити будувати такі графіки, треба володіти прийомами побудови графіків елементарних функцій, а також розуміти означення модуля числа.
Побудова графіків функції , що містять модуль
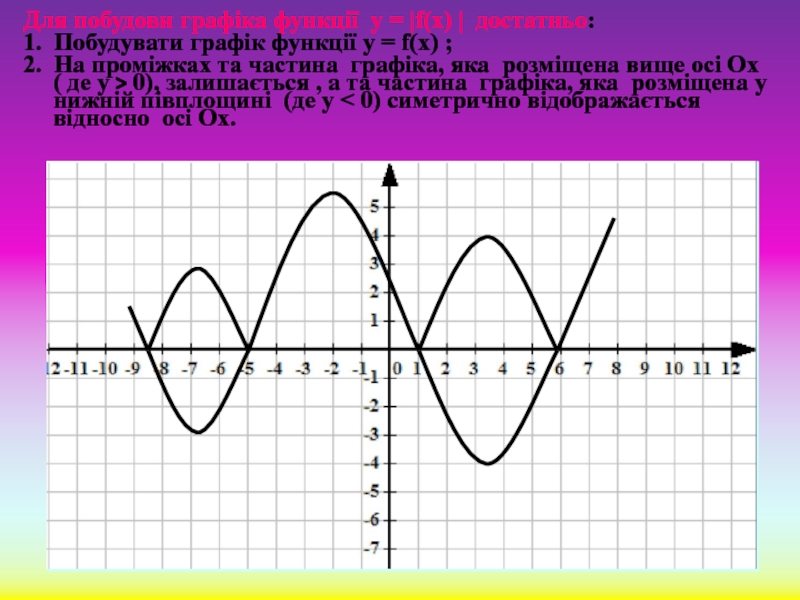
Слайд 10Для побудови графіка функції у = |f(х) | достатньо:
1. Побудувати графік
2. На проміжках та частина графіка, яка розміщена вище осі Ох ( де у > 0), залишається , а та частина графіка, яка розміщена у нижній півплощині (де у < 0) симетрично відображається відносно осі Ох.
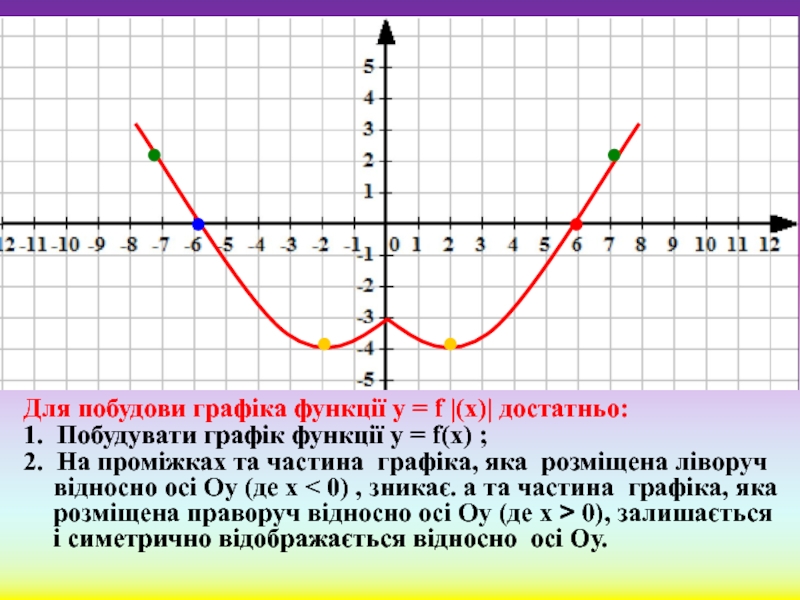
Слайд 11Для побудови графіка функції у = f |(х)| достатньо:
1. Побудувати
2. На проміжках та частина графіка, яка розміщена ліворуч відносно осі Оу (де х < 0) , зникає. а та частина графіка, яка розміщена праворуч відносно осі Оу (де х > 0), залишається і симетрично відображається відносно осі Оу.
1. построить график функции у = f(х) для х>0;
2. Та частина графіка, де х<0,зникає.
3. Ту частину графіка , де х>0 симметрично отразить построенную часть относительно оси ОУ.
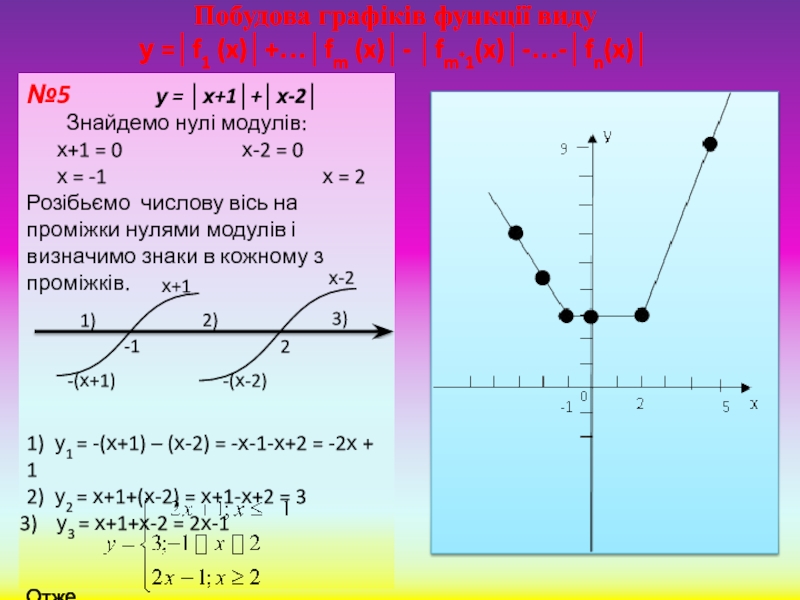
Слайд 15Побудова графіків функції виду
у =│f1 (x)│+…│fm (x)│- │fm+1(x)│-…-│fn(x)│
№5
Знайдемо нулі модулів:
х+1 = 0 х-2 = 0
х = -1 х = 2
Розібьємо числову вісь на проміжки нулями модулів і визначимо знаки в кожному з проміжків.
1) у1 = -(х+1) – (х-2) = -х-1-х+2 = -2х + 1
2) у2 = х+1+(х-2) = х+1-х+2 = 3
у3 = х+1+х-2 = 2х-1
Отже
1)
2)
3)
2
-1
-(х+1)
-(х-2)
х-2
х+1
Слайд 16Завдання для самостійного розв'язання:
Розв'язати рівняння:
1) │х+1│-│2х-5│ = 2
2) │2х+1│-│х-2│ = 1 відповідь : {-4; }
3) │3-2х│-3│х+4│ = 5х+1 відповідь : {-1}
4) │2х-1│ = 3 - 2│х+1│ відповідь : [-1; ]
5) │х-2│-1 = │х-3│ відповідь : х ≥ 3
6) 3∙│2х+1│+│2-х│ = 5│х+1│ відповідь : [- ;2]
Розв'язати нерівності:
1) 2│х+1│ < │х-2│+3х+1 відповідь : (- ;+∞)
2) │х+5│+1 > │2х-5│ відповідь : (- ; 11)
Побудувати графіки функцій: