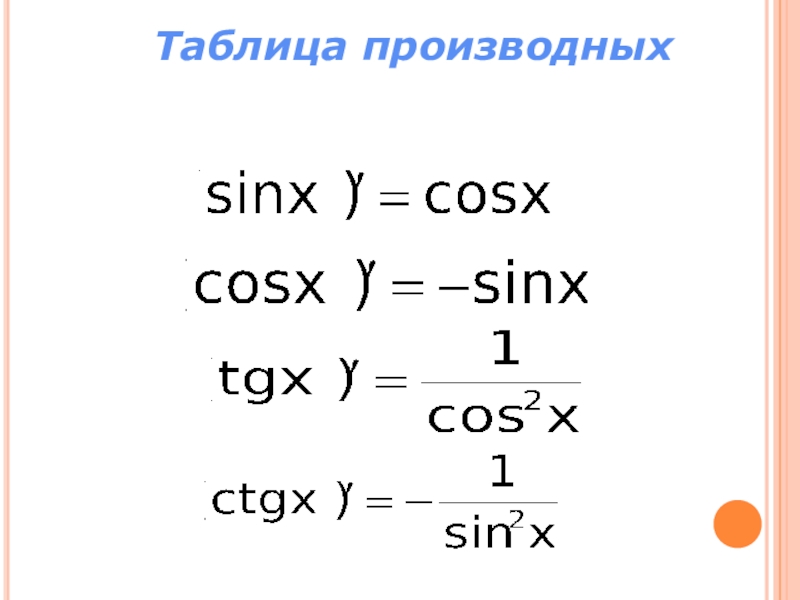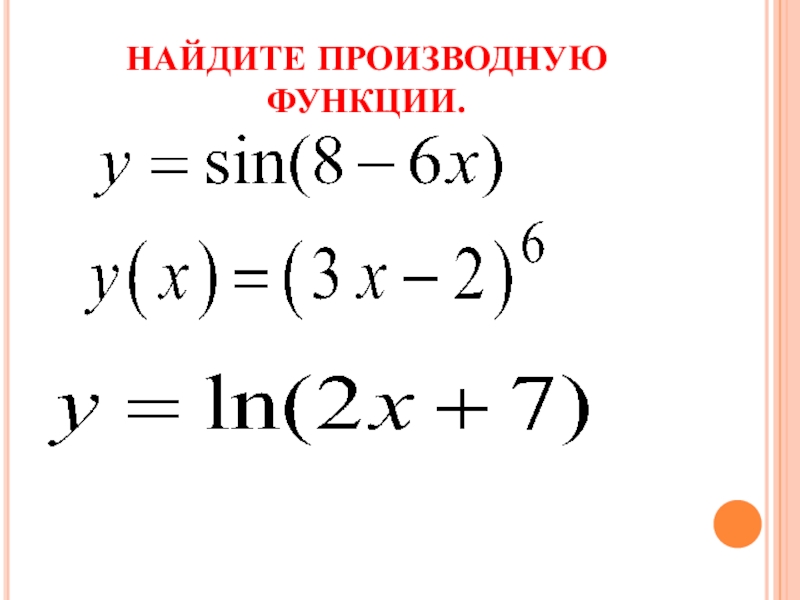ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока в11классе по теме Геометрический смысл производной
Содержание
- 1. Презентация урока в11классе по теме Геометрический смысл производной
- 2. ЦЕЛИ УРОКА: 1)Образовательные: повторить и
- 3. КРОССВОРД
- 4. ВОПРОСЫ1. Расстояние между двумя точками, измеренное вдоль
- 5. 6. Изменение положения тела в пространстве относительно
- 6. Слайд 6
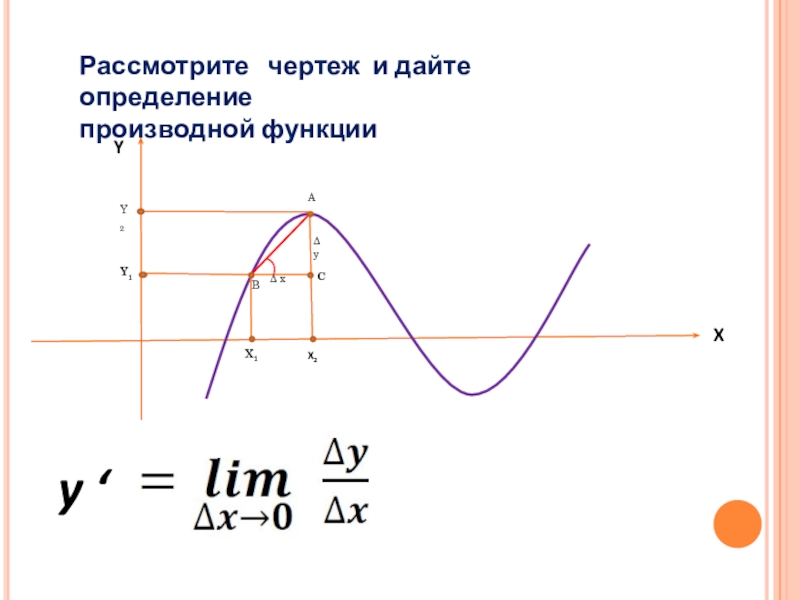
- 7. Δ xΔ yX1 X2 Y1 Y2ACBXY
- 8. Таблица производных
- 9. Таблица производных
- 10. Правила дифференцирования
- 11. АСВtg A-?tg В -?47АВСНайдите градусную меру <
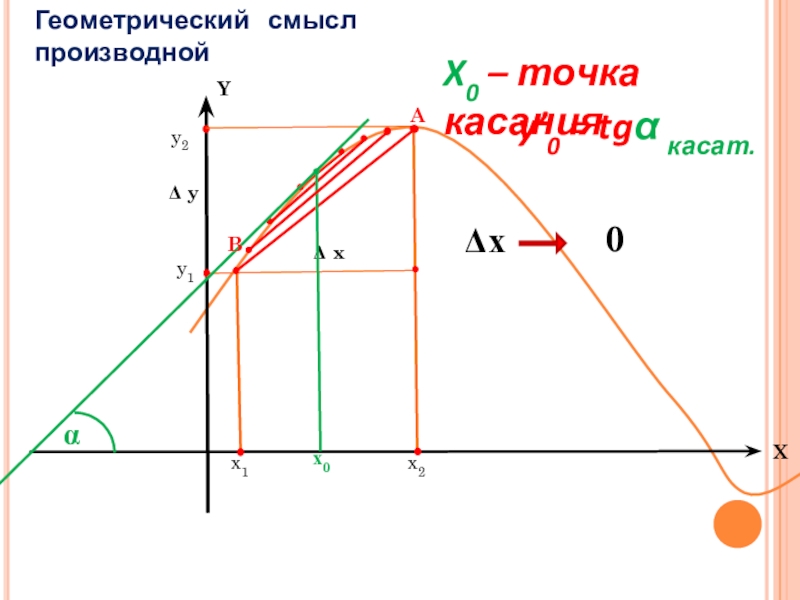
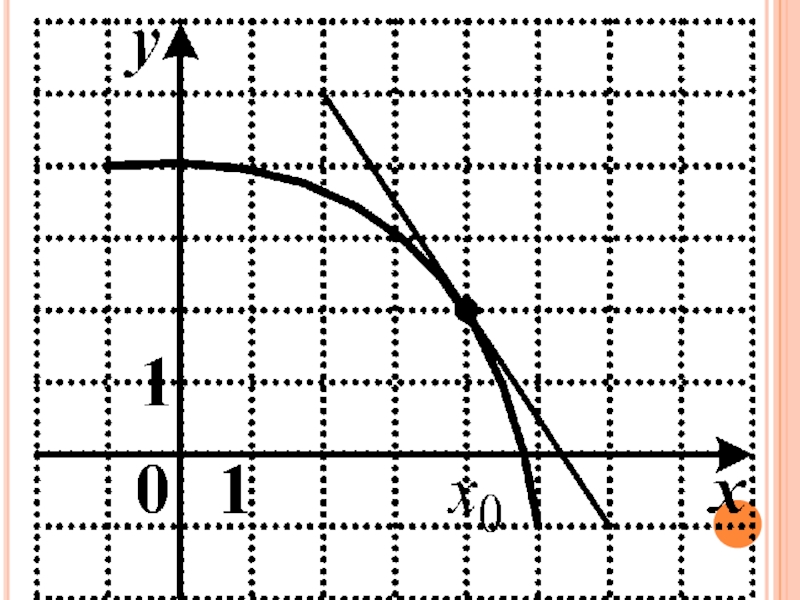
- 12. Геометрический смысл производнойAΔх0х0X0 – точка касанияy’0 = tgα касат.αB
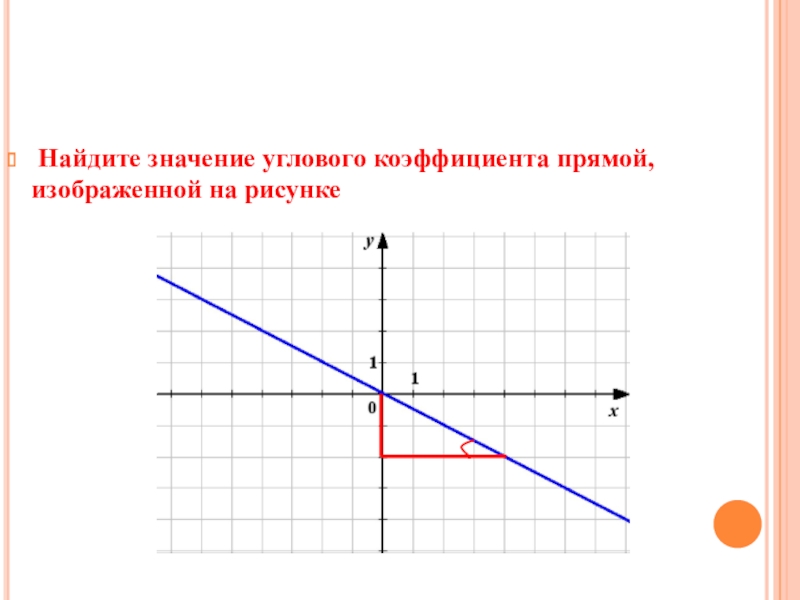
- 13. Найдите значение углового коэффициента прямой, изображенной на рисунке
- 14. Для вычисления углового коэффициента касательной, где k
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
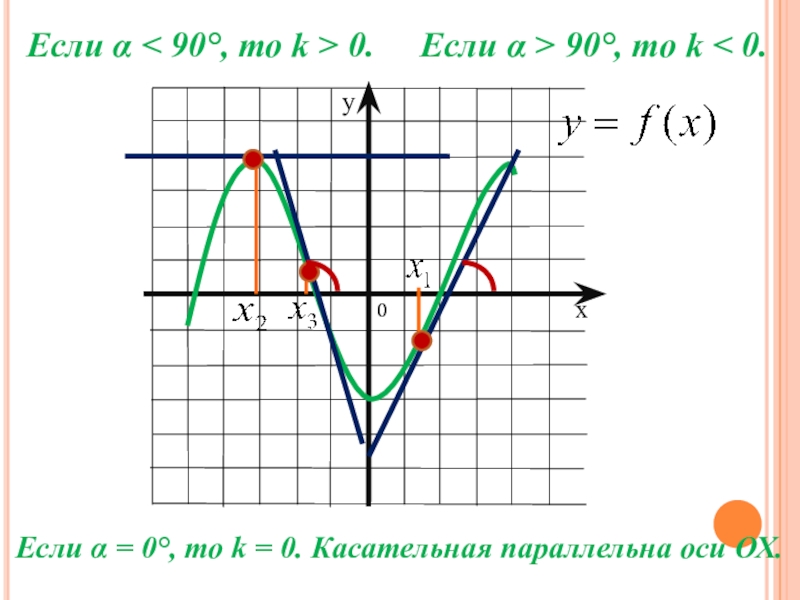
- 18. Если α < 90°, то k >
- 19. ЗАДАНИЕ 1. НАЙДИТЕ ПРОИЗВОДНУЮ ФУНКЦИИ.
- 20. НАЙДИТЕ ПРОИЗВОДНУЮ ФУНКЦИИ.
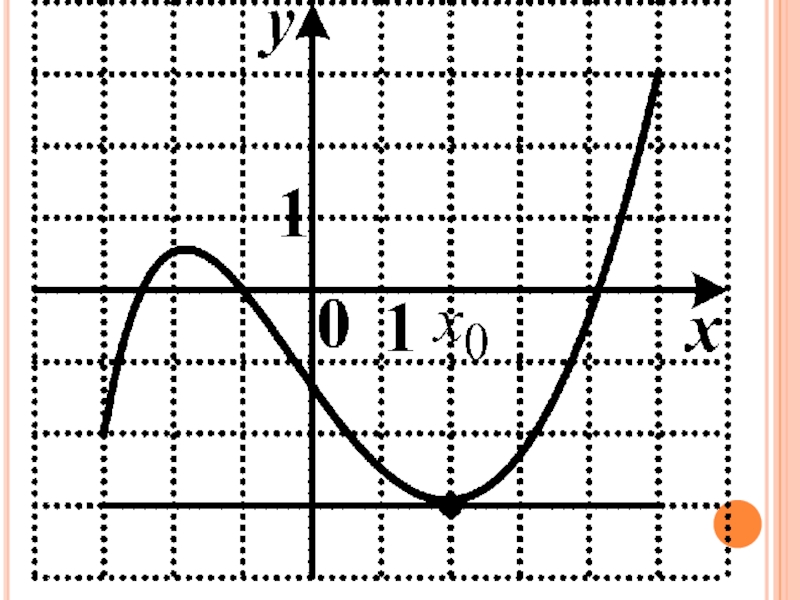
- 21. 10142Задание №2.На рисунке изображён график функции y
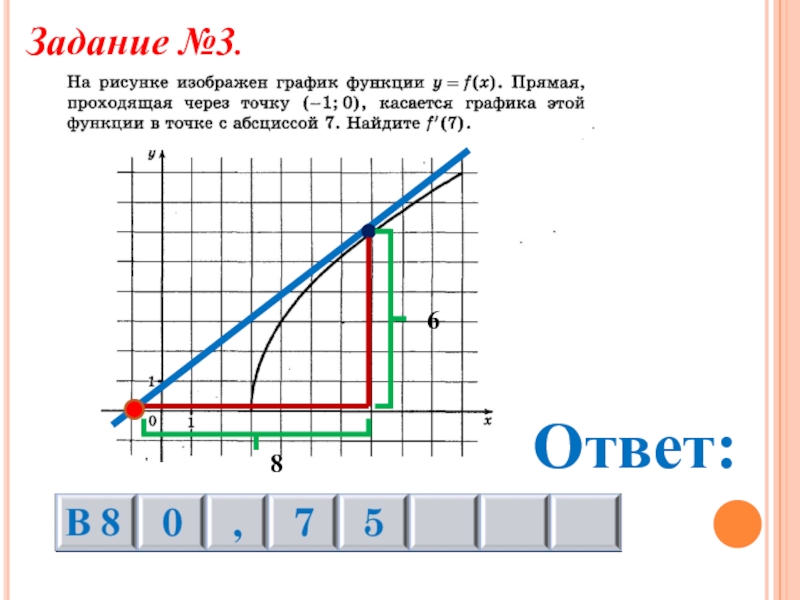
- 22. Задание №3.Ответ:68
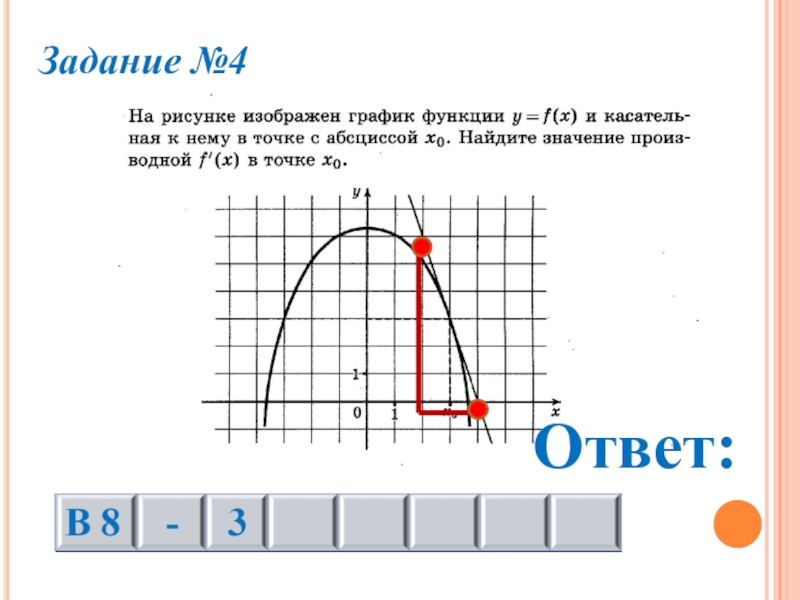
- 23. Задание №4Ответ:
- 24. На рисунке изображён график производной функции y
- 25. Задание №6К графику функции y = f(x)
- 26. Задание №70113К графику функции y = f(x)проведена
- 27. Задание №60113К графику функции y = f(x)проведена
- 28. САМОСТОЯТЕЛЬНАЯ РАБОТА РАЗНОУРОВНЕВАЯ
- 29. ОТВЕТЫ(1 УРОВЕНЬ)
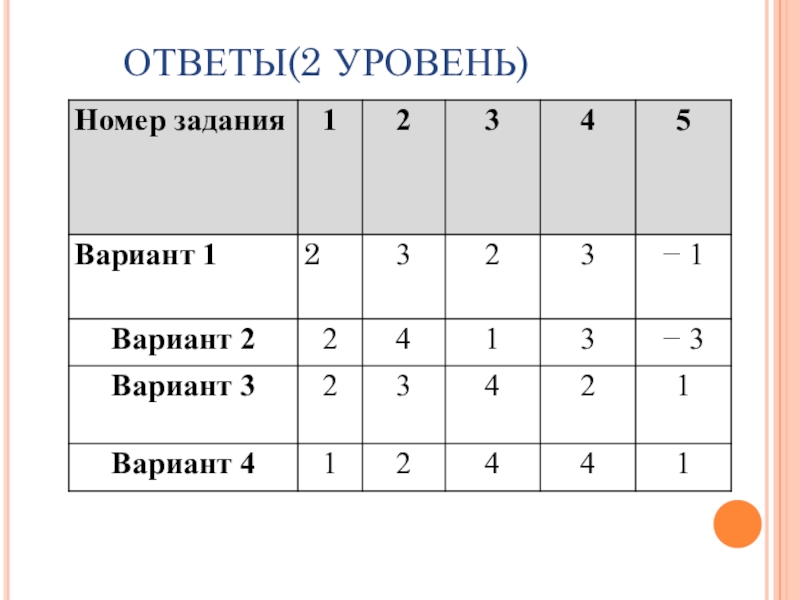
- 30. ОТВЕТЫ(2 УРОВЕНЬ)
- 31. РЕФЛЕКСИЯКакие типы задач мы рассмотрели?(задачи на применение
- 32. Домашнее заданиеВ отдельной тетради решить задания из
ЦЕЛИ УРОКА: 1)Образовательные: повторить и обобщить теоретический материал по теме «Геометрический смысл производной». Применение производной», рассмотреть решения типичных задач; 2)Воспитательные: формировать умение оценивать свой уровень знаний и стремление его повышать. 3)Развивающие: развивать умение анализировать
Слайд 1Подготовила учитель математики МБОУ «Левженская СОШ» Рузаевского муниципального района Рузаева Елена
Борисовна
Слайд 2 ЦЕЛИ УРОКА:
1)Образовательные: повторить и обобщить теоретический материал по теме
«Геометрический смысл производной». Применение производной», рассмотреть решения типичных задач;
2)Воспитательные: формировать умение оценивать свой уровень знаний и стремление его повышать.
3)Развивающие: развивать умение анализировать и систематизировать имеющуюся информацию;
2)Воспитательные: формировать умение оценивать свой уровень знаний и стремление его повышать.
3)Развивающие: развивать умение анализировать и систематизировать имеющуюся информацию;
Слайд 4ВОПРОСЫ
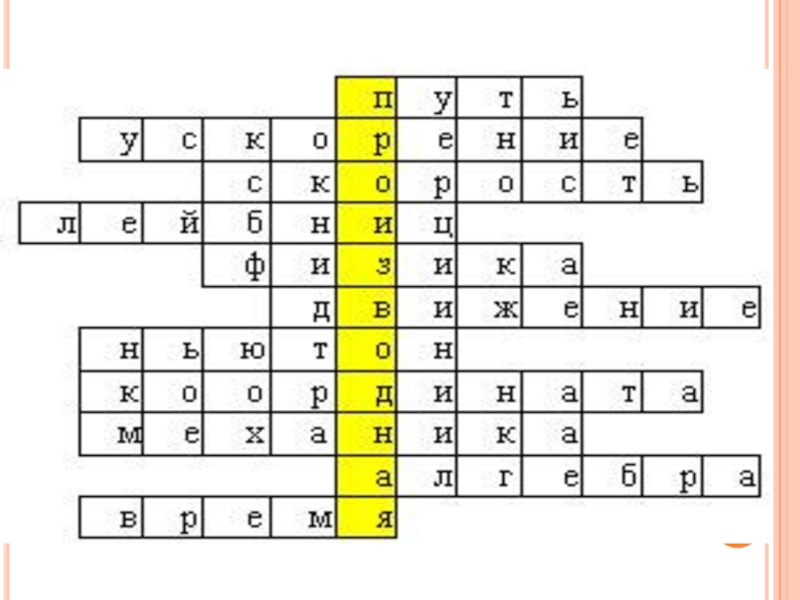
1. Расстояние между двумя точками, измеренное вдоль траектории движущегося тела.
2. Физическая
величина, характеризирующая быстроту изменения скорости .
3. Одна из основных характеристик движения .
4. Немецкий философ, математик, физик, один из создателей математического анализа .
5. Наука, изучающая наиболее общие закономерности явлений природы, состав и строение материи, законы ее движения .
Слайд 56. Изменение положения тела в пространстве относительно некоторой системы отсчета с
течением времени.
7. Выдающийся английский физик, именем которого названы основные законы механики .
8. Какие величины определяют положение тела в выбранной системе отсчета .
9. Физическая теория, устанавливающая закономерности взаимных перемещений тел в пространстве, и происходящих при этом взаимодействий .
10. Наука, изучающая применение производных в физике .
11. То, чего не достает в определении: производная от координаты по … есть скорость .
Слайд 11
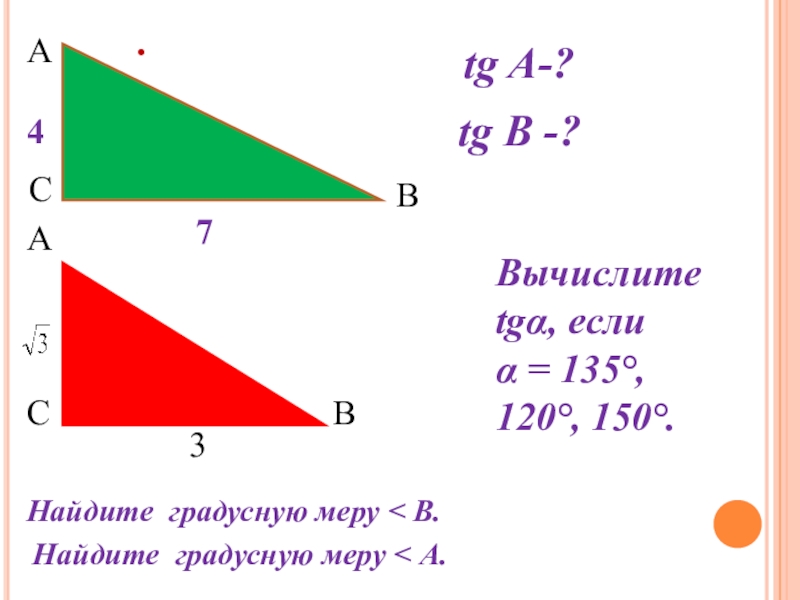
А
С
В
tg A-?
tg В -?
4
7
А
В
С
Найдите градусную меру < В.
3
Найдите градусную меру
А.
.
Вычислите tgα, если
α = 135°, 120°, 150°.
Слайд 14Для вычисления углового коэффициента касательной, где k = tgα, достаточно найти
отрезок касательной с концами в вершинах клеток и, считая его гипотенузой прямоугольного треугольника, найти отношение катет
Слайд 18
Если α < 90°, то k > 0.
Если α > 90°,
то k < 0.
Если α = 0°, то k = 0. Касательная параллельна оси ОХ.
0
Слайд 211
0
1
4
2
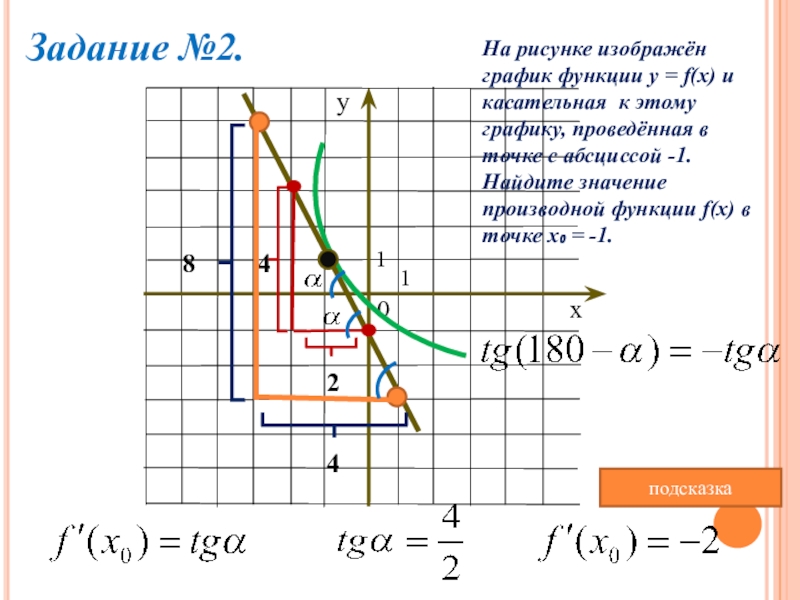
Задание №2.
На рисунке изображён график функции y = f(x) и
касательная
к этому графику, проведённая в точке с абсциссой -1. Найдите значение производной функции f(x) в точке х₀ = -1.
подсказка
4
8
Слайд 24
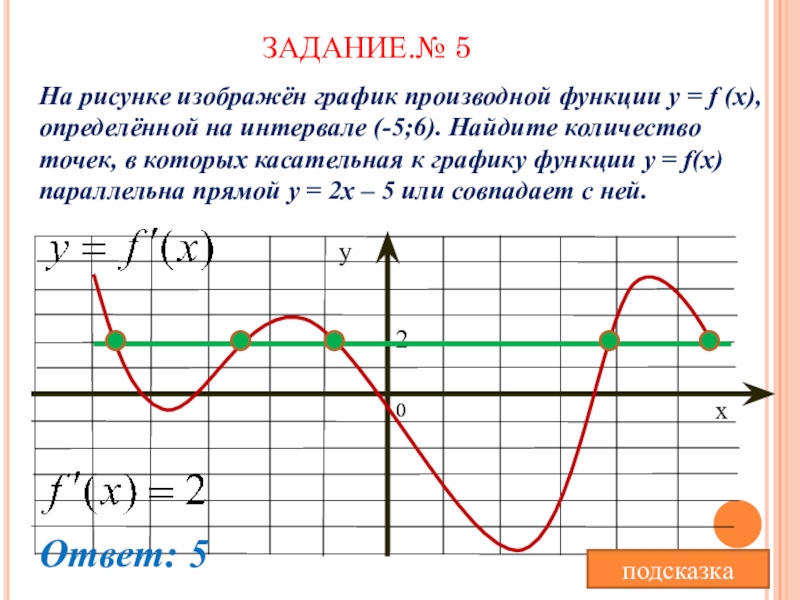
На рисунке изображён график производной функции y = f (x), определённой
на интервале (-5;6). Найдите количество точек, в которых касательная к графику функции y = f(x) параллельна прямой у = 2х – 5 или совпадает с ней.
подсказка
2
Ответ: 5
0
ЗАДАНИЕ.№ 5
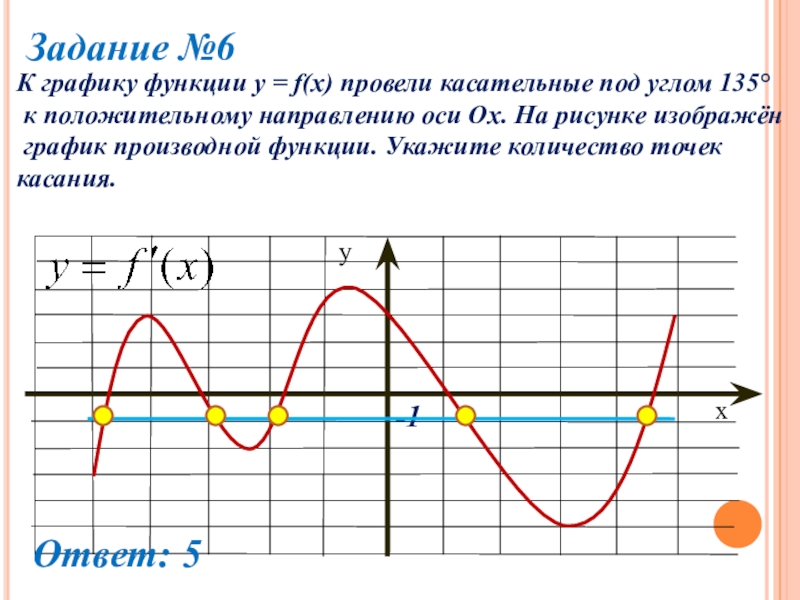
Слайд 25Задание №6
К графику функции y = f(x) провели касательные под углом
135°
к положительному направлению оси Ох. На рисунке изображён
график производной функции. Укажите количество точек
касания.
к положительному направлению оси Ох. На рисунке изображён
график производной функции. Укажите количество точек
касания.
-1
Ответ: 5
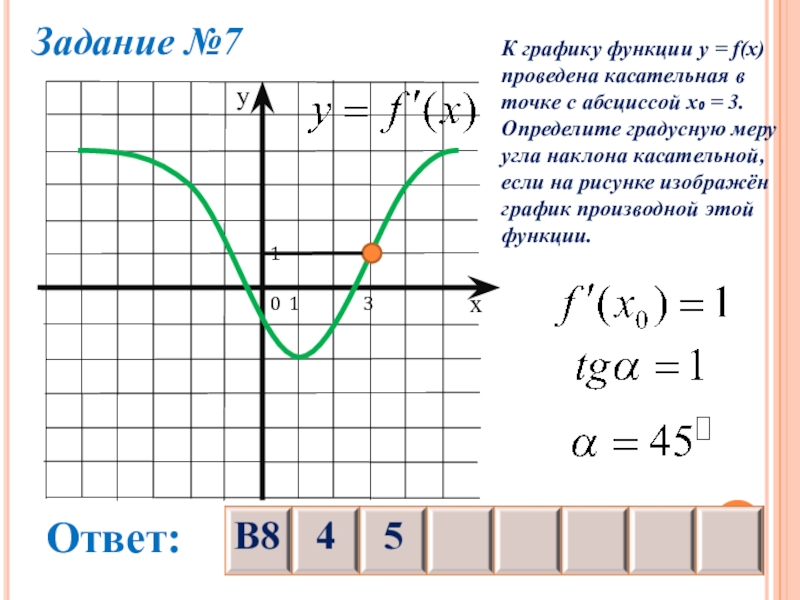
Слайд 26Задание №7
0
1
1
3
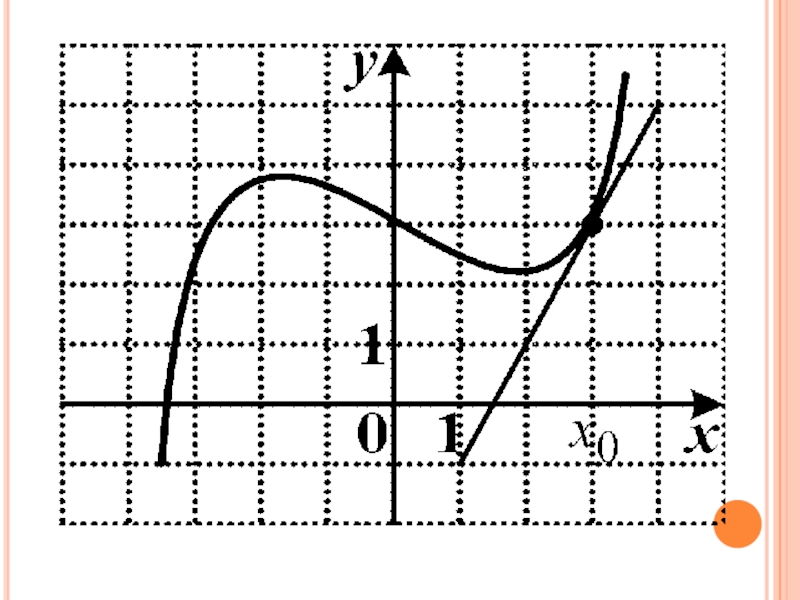
К графику функции y = f(x)
проведена касательная в
точке с
абсциссой х₀ = 3.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
Ответ:
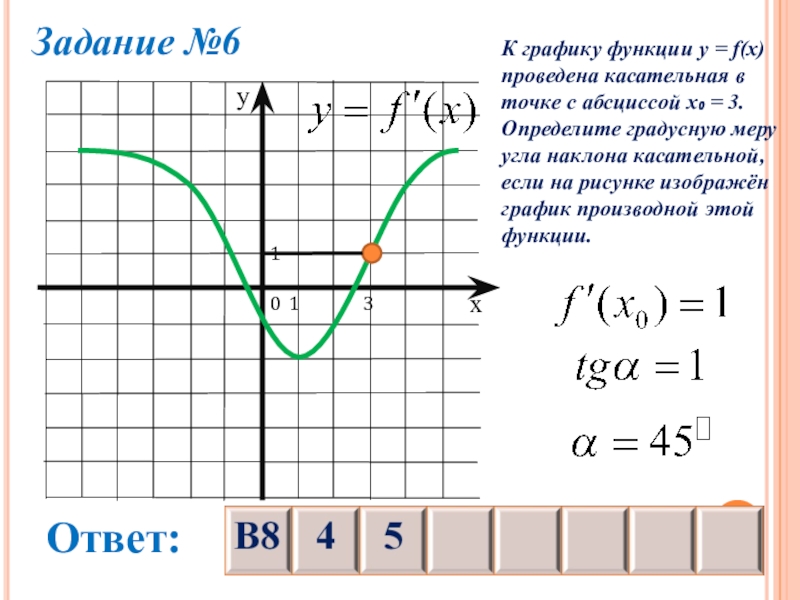
Слайд 27Задание №6
0
1
1
3
К графику функции y = f(x)
проведена касательная в
точке с
абсциссой х₀ = 3.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
Определите градусную меру
угла наклона касательной,
если на рисунке изображён
график производной этой
функции.
Ответ:
Слайд 31РЕФЛЕКСИЯ
Какие типы задач мы рассмотрели?
(задачи на применение геометрического смысла производной по
заданному графику функции или графику производной функции)
Какие знания использовали для решения задач?
(геометрический смысл производной, значение тангенса угла наклона прямой к оси Ох, условие параллельности прямых)
Какие способы мыслительной деятельности при решении задачи использовали?
(анализ, синтез, обобщение, освоение техники перевода проблемы в задачу, моделирование объекта задачи, выстраивание шагов решения, конструирование способов решения)
Какие знания использовали для решения задач?
(геометрический смысл производной, значение тангенса угла наклона прямой к оси Ох, условие параллельности прямых)
Какие способы мыслительной деятельности при решении задачи использовали?
(анализ, синтез, обобщение, освоение техники перевода проблемы в задачу, моделирование объекта задачи, выстраивание шагов решения, конструирование способов решения)
Слайд 32Домашнее задание
В отдельной тетради решить задания из прототипов В8 открытого банка
заданий ЕГ
Решить задачу Написать уравнение касательной к графику функции , проходящей через точку А(2; -5).
Решить задачу Написать уравнение касательной к графику функции , проходящей через точку А(2; -5).