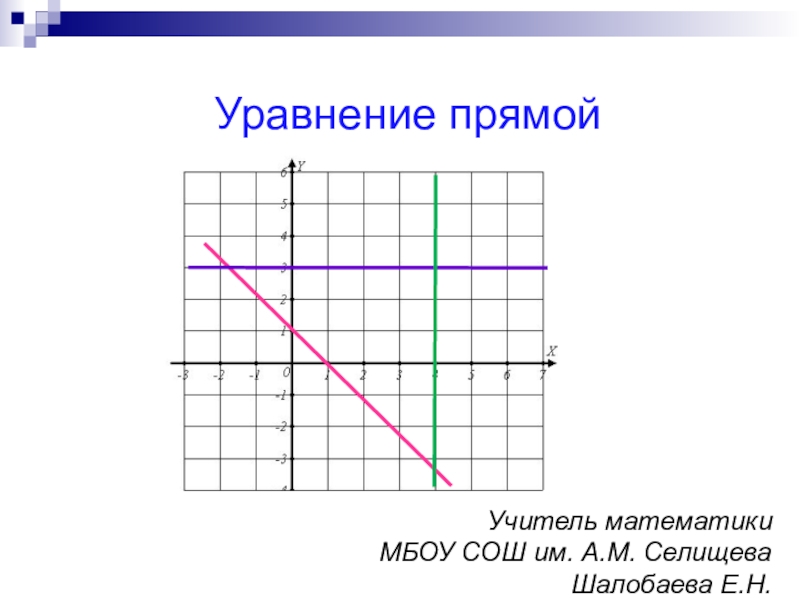
Презентация, доклад урока по теме Уравнение прямой

Содержание

1. Презентация урока по теме Уравнение прямой
2. Отметим на координатной плоскости точки А и
3. Получим уравнение:Если точка M не лежит на
4. Слайд 4
5. Слайд 5
6. Задача Написать уравнение прямой, проходящей через точки и . Ответ:
7. Слайд 7
8. Слайд 8
9. Домашнее заданиеп. 86–92; вопросы 1–21, с. 249; 972 (б, в)

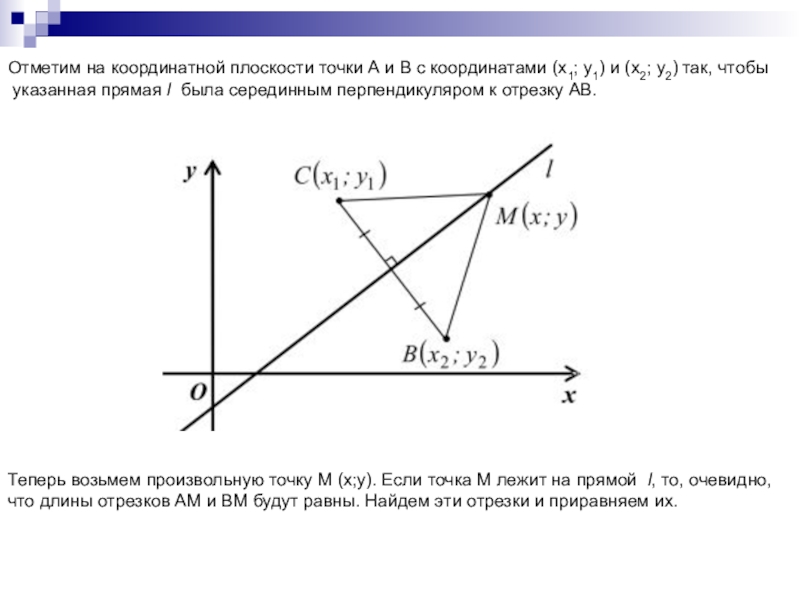
Отметим на координатной плоскости точки А и В с координатами (x1; y1) и (x2; y2) так, чтобы указанная прямая l была серединным перпендикуляром к отрезку AB.Теперь возьмем произвольную точку M (x;y). Если точка M лежит на

Главная
Алгебра
Презентация урока по теме Уравнение прямой

Слайд 1 Уравнение прямой
Учитель математики
МБОУ СОШ им. А.М. Селищева
Шалобаева Е.Н.

Слайд 2Отметим на координатной плоскости точки А и В с координатами (x1;

y1) и (x2; y2) так, чтобы
указанная прямая l была серединным перпендикуляром к отрезку AB.

Теперь возьмем произвольную точку M (x;y). Если точка M лежит на прямой l, то, очевидно,
что длины отрезков AM и BM будут равны. Найдем эти отрезки и приравняем их.

Отметим на координатной плоскости точки А и В с координатами (x1; y1) и (x2; y2) так, чтобы

Слайд 3Получим уравнение:
Если точка M не лежит на прямой, то, очевидно, что

отрезки AM и BM не будут
равны и координаты точки M не будут удовлетворять этому уравнению.
Значит, в прямоугольной системе координат уравнение прямой l имеет вид:

Раскроем скобки и выполним элементарные преобразования. Введем замену.

Получим уравнение