- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока по теме Числовые последовательности, 9 класс
Содержание
- 1. Презентация урока по теме Числовые последовательности, 9 класс
- 2. Числовая последовательность и способы ее заданияАрифметическая прогрессияГеометрическаяпрогрессияМетод математическойиндукцииЧисловые последовательности
- 3. Михаил Васильевич Ломоносов«Науки юношей питают, Отраду старым
- 4. Михаил Васильевич Ломоносов (1711-1765), русский просветитель, ученый-энциклопедист,
- 5. В начале 1736 года как один из
- 6. М.В. Ломоносов активно и успешно занимался астрономией,
- 7. Ломоносова по праву называют отцом русской
- 8. Цель нашего визита: Мы познакомимся с понятием
- 9. Последовательность - одно из самых основных понятий
- 10. Последовательность может быть составлена из чисел, точек,
- 11. Во многих семьях есть обычай, своего рода
- 12. Какие события происходят в наше жизни последовательно
- 13. 1.Какие события происходят в нашей жизни последовательно
- 14. Дни неделиНазвания месяцевКлассы в школеНомер счёта в
- 15. 1.Какие события происходят в нашей жизни последовательно
- 16. Найдите закономерности и покажите их с
- 17. Рассмотренные числовые ряды – примеры числовых последовательностейФункция
- 18. Задания для устной работы Назовите в последовательности
- 19. Способы задания последовательностейСловесный.(уп)- последовательность натуральных чисел, кратных трём.(уп): 3, 6, 9, 12, 15, :Табличный.
- 20. Графический
- 21. Аналитический.Указать формулу п-ого члена последовательности (уп =
- 22. Числа Фибоначчи х1 =х2=1;
- 23. 11112113311464115101051Связь между числами Фибоначчи и треугольником
- 24. В начале XIII века в городе Пизе
- 25. Французский религиозный философ, писатель, математик и физик
- 26. Первый математический трактат Практат «Опыт теории конических
- 27. Вариант__1______________№1. Найдите пять первых членов последовательности, кратных
- 28. Что такое последовательность?Какие виды последовательностей вы узнали?Какие
- 29. Домашнее задание№ 151,153,157Написать эссе о проведенном урокеИзучить
- 30. Слайд 30
Слайд 2Числовая последовательность
и способы ее задания
Арифметическая
прогрессия
Геометрическая
прогрессия
Метод математической
индукции
Числовые последовательности
Слайд 3Михаил Васильевич Ломоносов
«Науки юношей питают,
Отраду старым подают…
Науки пользуют везде,
Среди
В градском шуму и наедине,
В покое сладки и в труде»
М.В. Ломоносов
Слайд 4Михаил Васильевич Ломоносов (1711-1765), русский просветитель, ученый-энциклопедист, поэт, переводчик. Родился 8
В январе 1731 года Ломоносов, выдав себя за дворянского сына, поступил в Московскую славяно-греко-латинскую академию, где получил хорошую подготовку по древним языкам и другим гуманитарным наукам. Латинский язык знал в совершенстве, впоследствии был признан одним из лучших латинистов Европы.
Слайд 5В начале 1736 года как один из лучших студентов Ломоносов был
В 1739 году отправился во Фрайбург, где изучал химию и горное дело в Горной академии. К этому времени относятся первые поэтические и литературно-теоретические опыты. Ломоносов прислал в Россию "Письмо о правилах российского стихотворства" с приложенной к нему одой "На взятие Хотина", в которой практически подтверждал провозглашенные в "Письме" правила русского силлабо-тонического стихосложения.
Слайд 6М.В. Ломоносов активно и успешно занимался астрономией, мореходным делом, краеведением, географией,
Слайд 7 Ломоносова по праву называют отцом русской океанографии, в этой науке,
Жизнь и творчество таких, как Ломоносов показывает нам, как многого может достичь человеческая личность)
Слайд 8Цель нашего визита:
Мы познакомимся с понятием " числовая последовательность", узнаем,
( ее виды), познакомимся со знаменитыми последовательностями, и рассмотрим способы задания последовательностей.
Слайд 9Последовательность - одно из самых основных понятий математики.
Понятием последовательности, прогрессии,
Слайд 10Последовательность может быть составлена из чисел, точек, функций, векторов и т.д.
линейная
квадратичная функция у = ах2+вх+с,
прямая пропорциональность
у = кх,
обратная пропорциональность у =1/х ,
кубическая функция у = х3,
функция у =|х|.
Слайд 11Во многих семьях есть обычай, своего рода ритуал: в день рождения
На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день, 2 день, 3 день, 4 день
Эти примеры-примеры числовых последовательностей
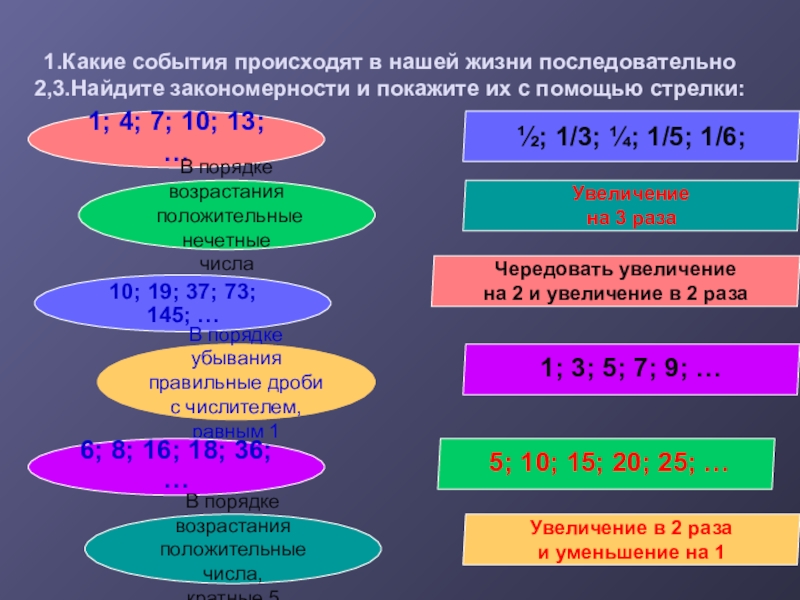
Слайд 131.Какие события происходят в нашей жизни последовательно 2,3.Найдите закономерности и покажите их
1; 4; 7; 10; 13; …
В порядке возрастания
положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3 раза
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
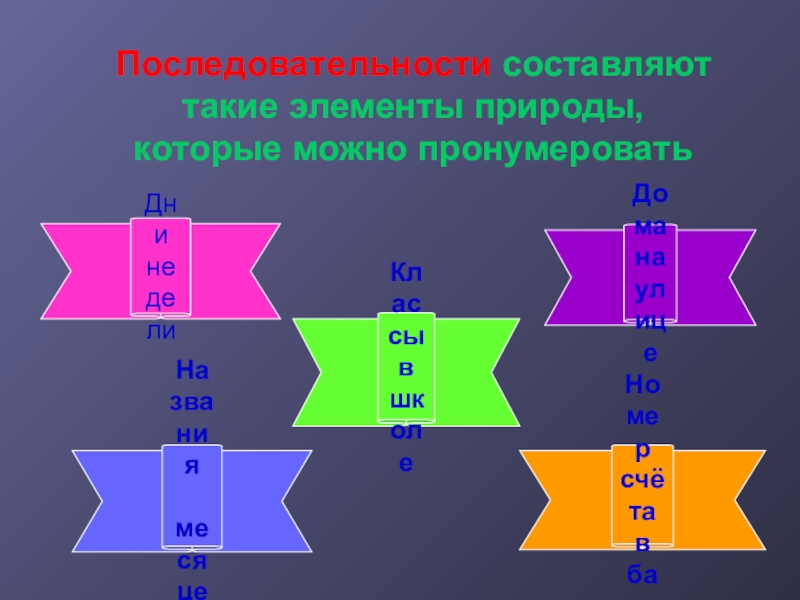
Слайд 14Дни
недели
Названия
месяцев
Классы
в школе
Номер
счёта
в банке
Дома
на улице
Последовательности составляют
такие
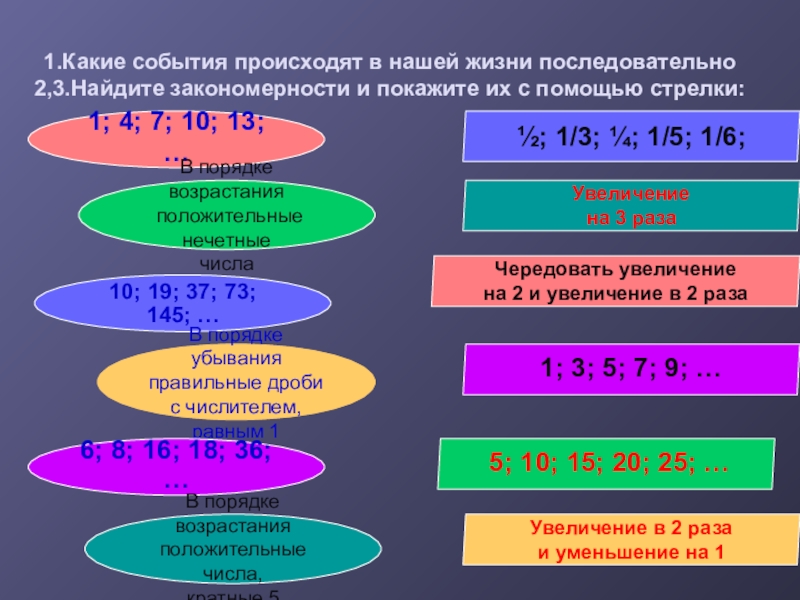
Слайд 151.Какие события происходят в нашей жизни последовательно 2,3.Найдите закономерности и покажите их
1; 4; 7; 10; 13; …
В порядке возрастания
положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3 раза
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
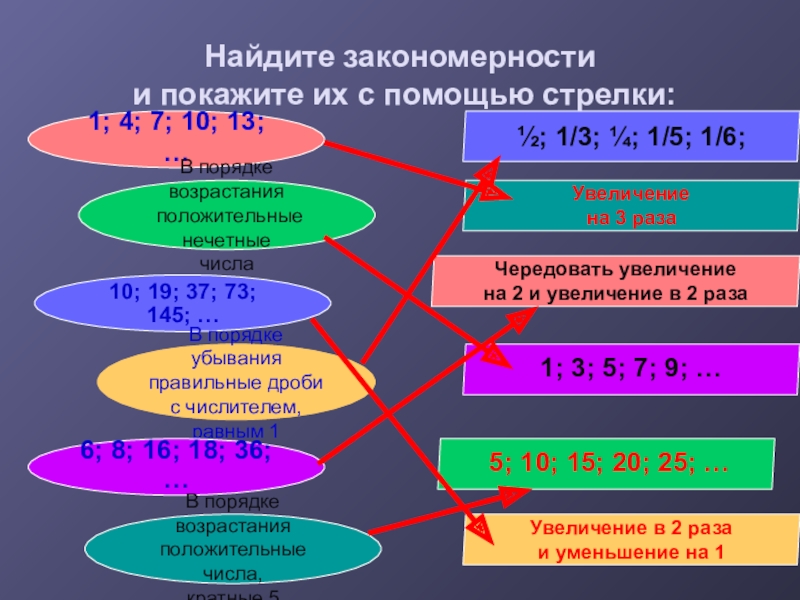
Слайд 16Найдите закономерности
и покажите их с помощью стрелки:
1; 4; 7; 10;
В порядке возрастания
положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3 раза
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
Слайд 17Рассмотренные числовые ряды –
примеры числовых последовательностей
Функция натурального аргумента называется числовой
Обозначают члены последовательности так
а1; а2; а3; а4; … аn (ап)- последовательность, ап - п-ый член последовательности
1, 2, 3, 4, 5, …, п,-порядковый номер члена последовательности.
ап-1 -предыдущий член последовательности,
ап+1 - последующий член последовательности. Последовательности бывают конечными и бесконечными, возрастающие и убывающие, постоянные.
Вот примеры бесконечных числовых последовательностей, известных еще в древности:
1, 2, 3, 4, 5, : - последовательность натуральных чисел;
2, 4, 6, 8, 10, :- последовательность четных чисел;
1, 3, 5, 7, 9, : - последовательность нечетных чисел;
1, 4, 9, 16, 25, : - последовательность квадратов натуральных чисел;
2, 3, 5, 7, 11, : - последовательность простых чисел;
1,1/2 ,1/3 ,1/4 ,… :- последовательность чисел, обратных натуральным.
Последовательность целых положительных двузначных чисел, оканчивающихся на нуль: 10,20,30,40,50,60,70,80,90-является конечной последовательностью
Последовательность (ап)называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего, например1;1/2;1/3;..;1/п
Последовательность (ап)называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, например 0;1/2;2/3;…;п-1/п
Возрастающая и убывающая последовательности называются монотонными.
Последовательность, составленная только из одного числа, называется постоянной последовательностью., например: 5;5;5;…
Слайд 18Задания для устной работы
Назовите в последовательности 1; 1/2; 1/3; 1/4;
Является ли последовательность четырёхзначных чисел конечной?
Назовите её первый и последний члены.
Является ли последовательностью запись чисел 2; 4; 7; 1; -21; -15; …?
Слайд 19Способы задания последовательностей
Словесный.
(уп)- последовательность натуральных чисел, кратных трём.
(уп): 3, 6, 9,
Табличный.
Слайд 21Аналитический.
Указать формулу п-ого члена последовательности (уп = 3п)
Формула общего члена
х5=3.5+2=17;
х45=3.45+2=137.
Рекуррентный (от латинского - возвращаться).
Это формула, выражающая любой член последовательности, начиная с некоторого, через предыдущие (уп = уп-1 + 3).
Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие (один или несколько), называют рекуррентной (от латинского слова recurro– возвращаться).
Например, последовательность, заданную правилом
а1=1; аn+1= аn +3
можно записать с многоточием:
1; 4; 7; 10; 13; …
Слайд 22Числа Фибоначчи
х1 =х2=1; хn+2=xn+1 +xn;
Последовательность чисел Фибоначчи задается так:
Вычислим несколько
её первых членов:
1; 1; 2; 3; 5; 8; 13; 21;
34;55; 89; 144;
233; 377; …
Треугольник Паскаля
Бесконечная числовая таблица треугольной формы,
где по боковым сторонам стоят 1,
а каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа.
Слайд 231
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
Связь между числами Фибоначчи
и треугольником Паскаля
Между числами Фибоначчи
и треугольником
Для 1 диагонали – 1;
Для 2 диагонали – 1;
Для 3 диагонали – 1+1=2;
Для 4 диагонали – 1+2=3;
Для 5 диагонали – 1+3+1=5;
Для 6 диагонали – 1+4+3=8 ...
В результате мы получаем числа Фибоначчи: 1; 1; 2; 3; 5; 8; …
Всегда сумма чисел n-ой диагонали есть n-ое число Фибоначчи.
Слайд 24 В начале XIII века в городе Пизе (Италия) жил большой знаток
Слайд 25Французский религиозный философ, писатель, математик и физик Блез Паскаль родился в
Слайд 26Первый математический трактат Практат «Опыт теории конических сечений» (1639, издан 1640)
Слайд 27Вариант__1______________
№1. Найдите пять первых членов последовательности, кратных пяти
№2. Назовите члены последовательности
А)а103 и а106
__________________________________________
Б) аn+2 и аn+6
№3. Числовая последовательность задана аналитически формулой хn=n2+1. Найдите третий, четвертый и пятый члены этой последовательности.
№4. Выпишите первые четыре члена последовательности, если х1=1, хn= 2+хn-1, n=2,3,4
________________
№5. Перечислите известные вам способы задания числовой последовательности.
Вариант_2_______________
№1. Найдите пять первых членов последовательности, кратных трем
____________
№2. Назовите члены последовательности аn, которые расположены между:
А)а213 и а216
__________________________________________
Б) аn+6 и аn+10
№3. Числовая последовательность задана аналитически формулой хn=n2-15. Найдите третий, четвертый и пятый члены этой последовательности.
№4. Выпишите первые четыре члена последовательности, если х1=3, хn= хn-1-2, n=2,3,4
№5. Перечислите известные вам способы задания числовой последовательности.
_____________________________________________________________________________
Слайд 28
Что такое последовательность?
Какие виды последовательностей вы узнали?
Какие способы задания вы узнали?
О
Слайд 29Домашнее задание
№ 151,153,157
Написать эссе о проведенном уроке
Изучить информацию об обитателях подводного
( по желанию)