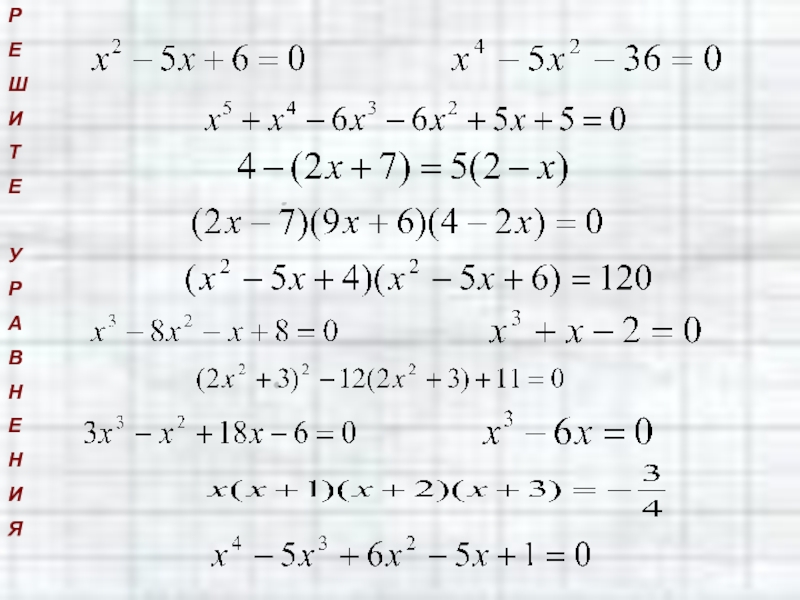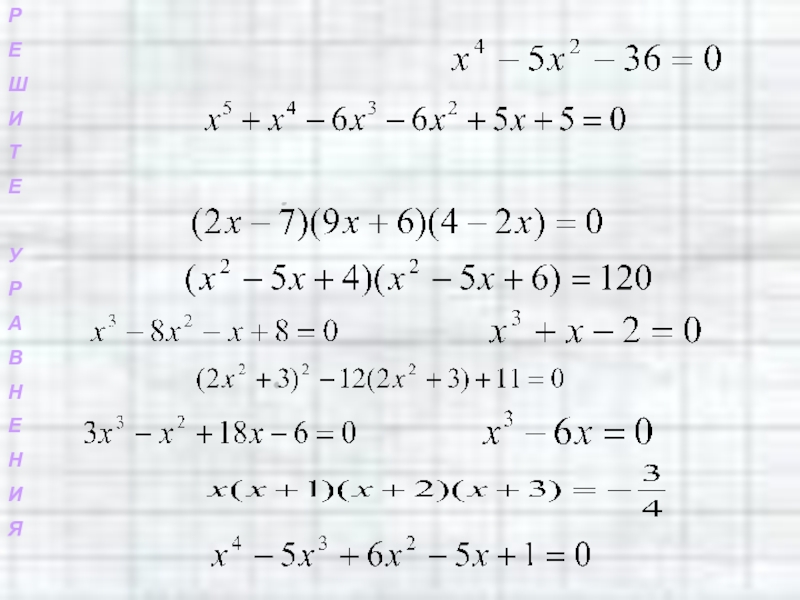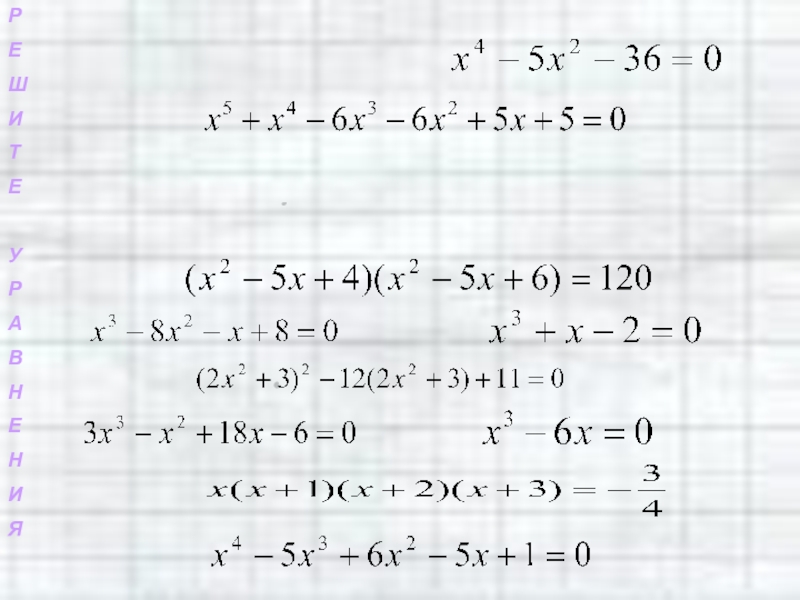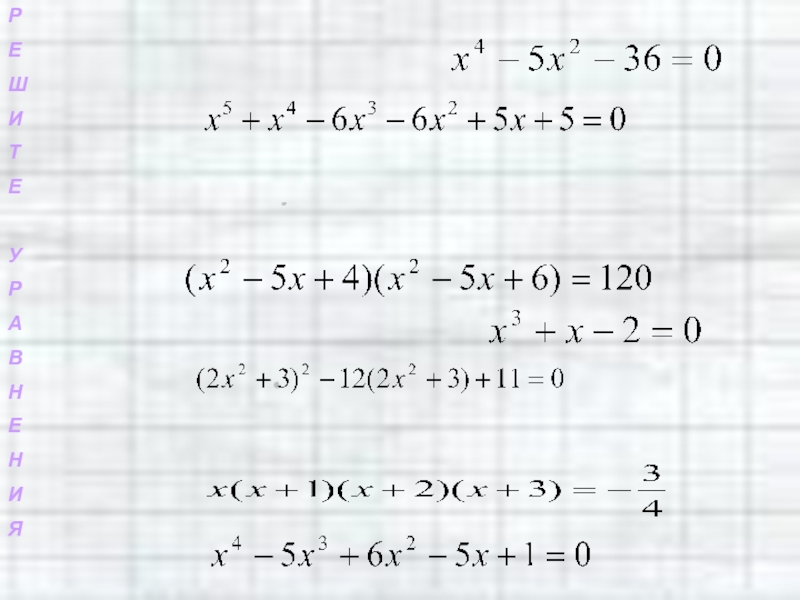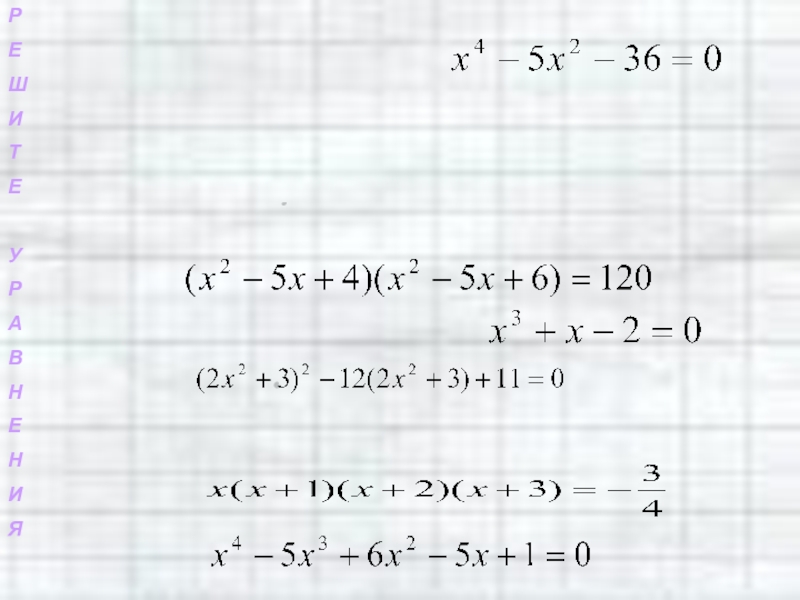Слайд 1Тема урока: «ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ»
Зачётная работа
слушателя курсов повышения
квалификации учителей математики
Павловской Светланы Фёдоровны,
учителя математики филиала МБОУ
«Трудовская школа» при ГБУЗ РК «КПБ №5»
----------------------------------------------------------------
Руководитель:
Матюшина Людмила Николаевна,
старший преподаватель кафедры
естественно-математического образования КРИППО
КРЫМСКИЙ РЕСПУБЛИКАНСКИЙ ИНСТИТУТ ПОСЛЕДИПЛОМНОГО ПЕДАГОГИЧЕСКОГО ОБРАЗОВАНИЯ
Кафедра естественно-математического образования
Слайд 3 Уравнения в школьном курсе алгебры занимают ведущее место.
На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники.
ВВЕДЕНИЕ.
Слайд 4На изучение темы «Целое уравнение и его корни» отводится 5 часов.
ОСНОВНАЯ
ЦЕЛЬ- сформировать умение решать некоторые виды целых уравнений, используя разложение многочлена на множители и введение новой переменной.
Слайд 5УРОК 1.
Тема. Целое уравнение и его корни.
Цель: ввести понятие целого
уравнения ,степени уравнения, познакомить учащихся с уравнениями высших степеней, повторить решение уравнений первой и второй степени.
УРОК 2.
Тема "Решение целых уравнений«
Цели: сформировать умение решать некоторые виды целых уравнений, используя разложение многочлена на множители, введение новой переменной и графически.
УРОК 3,4(2 часа).
Тема:"Решение целых уравнений»
Цели: обобщить и углубить сведения об уравнениях; закрепить умения и навыки решения целых уравнений систематизировать материал по данной теме.
УРОК 5.
Тема: «Решение целых уравнений»
Цели: закрепить знания, умения и навыки при решении уравнений высших степеней
Слайд 6Тема урока:
«Целое уравнение и его корни»
Тип урока: урок объяснения нового
материала.
Слайд 7ПЛАН УРОКА
Проверка домашнего задания.
(Фронтальный опрос)
2. Устная работа
(математическое домино)
3. Изучение нового материала
(Беседа
с элементами лекции)
4. Закрепление нового материала
(Вопросы. Решение № на доске и в тетрадях.
Самостоятельная работа с последующей проверкой)
5. Домашнее задание.
6. Подведение итогов урока.
Слайд 8Цели урока:
Образовательные: ввести понятие целого уравнения, степени уравнения, познакомить учащихся с
уравнениями высших степеней.
Развивающие: развитие мыслительной деятельности, внимания, развитие интереса к предмету, формирование потребностей к приобретению знаний.
Воспитательные: воспитывать у учащихся взаимоуважения, трудолюбия, навыков самоконтроля.
Слайд 9 ХОД УРОКА
Проверка домашнего задания.(Фронтальный опрос учащихся)
ПРОДОЛЖИТЬ ОТВЕТ
Уравнением называется …..
Корнем уравнения с одной переменной называется…
Решить уравнение –значит …
Уравнения с одной переменной , имеющие одни и те же корни, называются …
ПЕРЕЧИСЛИТЬ СВОЙСТВА РАВНОСИЛЬНОСТИ.
Слайд 10
Не всегда уравненья
Разрешают сомненья,
Но итогом сомненья
Может быть озаренье.
/А.Н.Колмогоров/
МАТЕМАТИЧЕСКОЕ ДОМИНО
Слайд 12Левая и правая части являются дробными выражениями.
Такие уравнения относятся к
дробным.
Слайд 13В ЭТИХ УРАВНЕНИЯХ ЛЕВАЯ И ПРАВЫЕ ЧАСТИ ЯВЛЯЮТСЯ ЦЕЛЫМИ ВЫРАЖЕНИЯМИ .
ТАКИЕ УРАВНЕНИЯ НАЗЫВАЮТСЯ ЦЕЛЫМИ.
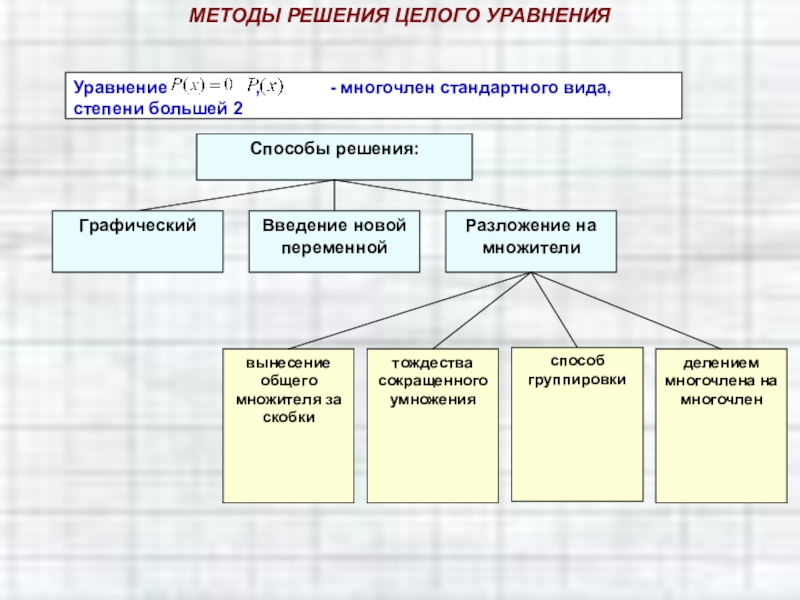
Слайд 14Для целых уравнений введём определение степени уравнения.
Если уравнение с одной переменной
записано в виде Р(х)=0, где Р(х)-многочлен стандартного вида, то степень этого многочлена называют степенью уравнения.
Степень произвольного целого уравнения называют степень равносильного ему уравнения вида Р(х)=0, где Р(х)-многочлен стандартного вида.
Слайд 16Приведём каждое уравнение к виду Р(х)=0, где Р(х) многочлен стандартного вида:
Слайд 19
Уравнение n-ой степени можно привести к общему виду:
Слайд 20Повторите алгоритм решения уравнений первой степени
Слайд 21КАК НАЗЫВАЮТСЯ УРАВНЕНИЯ ТАКОГО ВИДА?
КАК РЕШИТЬ КВАДРАТНОЕ УРАВНЕНИЕ?
СКОЛЬКО КОРНЕЙ МОЖЕТ ИМЕТЬ
КВАДРАТНОЕ УРАВНЕНИЕ?
СДЕЛАЙТЕ ВЫВОД О КОЛИЧЕСТВЕ КОРНЕЙ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ.
Уравнение второй степени
Слайд 221. Вычислить дискриминант по формуле:
2. Если
то квадратное уравнение не
имеет корней.
3. Если
то квадратное уравнение имеет один корень:
4. Если
то квадратное уравнение имеет два корня:
Алгоритм решения квадратного уравнения
В случае если b – четное число, то:
Уравнение вида
является приведенным квадратным уравнением.
Если числа таковы, что то эти числа – корни уравнения.
С помощью этого утверждения, а точнее утверждения, обратного теореме Виета можно решать приведенные квадратные уравнения
Слайд 23Для уравнений 3 и 4 степени известны формулы корней, но они
очень сложны и неудобны для практического применения.
Что касается уравнений пятой и более высоких степеней, то общих формул корней не существует.
Слайд 24Перед нами стоит задача: рассмотреть методы решения уравнений 3 , 4-й
и более высоких степени.
Слайд 25ПЕРЕХОДИМ К ЗАКРЕПЛЕНИЮ НОВОГО МАТЕРИАЛА
№265
1.Задание: Выполните устно
Как определить степень уравнения Р(х)=0?
Как
определить степень произвольного уравнения?
Слайд 26 Задание 2. Решите уравнение.
№266
Слайд 27САМОСТОЯТЕЛЬНАЯ РАБОТА.
Вариант 1. Вариант 2.
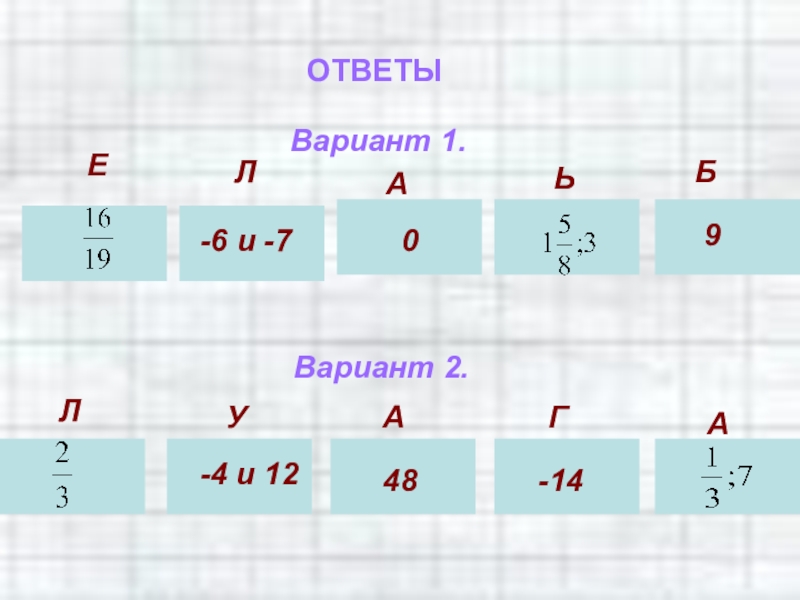
Слайд 28ОТВЕТЫ
Вариант 1.
Е
Л
-6 и -7
А
0
Ь
Б
9
Вариант 2.
Л
У
-4 и 12
А
48
Г
-14
А
Вариант 2.
Нильс Хенрик (1802—1829), норвежский математик, один из крупнейших математиков 19 в.. . Абель доказал , что алгебраические уравнения степени выше 4-й в общем случае неразрешимы в радикалах.
Эварист Галуа (1811-1832) Французский математик. Заложил основы современной алгебры. Нашёл необходимое и достаточное условие , которому удовлетворяет алгебраическое уравнение, разрешимое в радикалах.
Слайд 30ДОМАШНЕЕ ЗАДАНИЕ.
П. 12, стр 72-73.
№267
Повторить способы разложения многочлена на множители.
Стр 242
п.7
Повторить графики функций.
Стр 250 п.34-39
Слайд 31ИТОГ УРОКА.
Что нового вы узнали сегодня на уроке?
Какие уравнения называются целыми?
Как
определить степень целого уравнения?
Сколько корней может иметь уравнение первой степени? Уравнение второй степени?
Слайд 33Тема урока: "Решение целых уравнений"
Тип урока: урок объяснения нового материала.
Слайд 34Цели урока:
Образовательные: сформировать умение решать некоторые виды целых уравнений, используя разложение
многочлена на множители, введение новой переменной и графически.
Развивающие: развитие мыслительной деятельности, внимания, развитие интереса к предмету, формирование потребностей к приобретению знаний.
Воспитательные: воспитывать у учащихся взаимоуважения, трудолюбия, навыков самоконтроля.
Слайд 35План урока:
Постановка цели урока.
Проверка домашнего задания (тест)
Индивидуальная работа по карточкам
(у доски)
Фронтальный опрос учащихся (блиц-опрос)
Объяснение нового материала
Решение уравнений на доске и в тетрадях.
Подведение итогов урока.
Слайд 36Проверка домашнего задания.(7 мин)
Тест 1.
Вариант 1.
А1.Назовите степень уравнения
Четвёртая
Вторая
Первая
Седьмая
А2..Найдите корень уравнения
(5-х)(х+5)+х(х-10)=25
1)5
2)10
3)-2
4)0
В1. Решите уравнение.
В ответе укажите корень ,если корней несколько, то их сумму
Ответ :_______________
А1.Назовите степень уравнения
1) десятая
2) пятая
3)Первая
4)вторая
А2..Найдите корень уравнения
(7-х)(х+7)+х(х-14)=49
1)0
2)7
3)-14
4)-7
В1. Решите уравнение.
В ответе укажите корень ,если корней несколько, то их произведение
Ответ :_______________
Вариант 2.
Слайд 37Индивидуальная работа по карточкам.
Слайд 38БЛИЦ-ОПРОС.
(РАБОТА С КЛАССОМ.)
КАКОЕ УРАВНЕНИЕ НАЗЫВАЕТСЯ ЦЕЛЫМ?
ПРИВЕДИТЕ ПРИМЕР ЦЕЛОГО УРАВНЕНИЯ?
ЧТО НАЗЫВАЕТСЯ СТЕПЕНЬЮ
ЦЕЛОГО УРАВНЕНИЯ?
СКОЛЬКО КОРНЕЙ МОЖЕТ ИМЕТЬ ЦЕЛОЕ УРАВНЕНИЕ?
К КАКОМУ ВИДУ МОЖНО ПРИВЕСТИ УРАВНЕНИЕ ПЕРВОЙ СТЕПЕНИ?
К КАКОМУ ВИДУ МОЖНО ПРИВЕСТИ УРАВНЕНИЕ ВТОРОЙ СТЕПЕНИ?
Слайд 39Проверка работы учащихся у доски..
План ответа
К карточкам №1 и №2.
Назвать степень
уравнения.
К какому виду уравнение приведено.
Сколько корней может иметь уравнение данного вида.
Алгоритм решения
К карточке №3.
Назвать способы разложения на множители.
Слайд 40
2.Прямая
1.Кубическая парабола
4.Парабола
3.Гипербола
Установить соответствие
Слайд 41На прошлом уроке мы познакомились с понятием степени целого уравнения ,
научились определять степень целого уравнения и повторили решение уравнений первой и второй степеней
Из предложенных на слайде уравнений , найдите уравнения первой и второй степени и решите их устно.
Изучение нового материала.
Сегодня на уроке мы будем учиться решать уравнения более высоких степеней.
Слайд 43Какое из уравнений на слайде вы можете решить?
Слайд 45
Какое свойство вы использовали при решение этого уравнения?
Определим, уравнение какой степени
мы решили.
Слайд 46Мы решили уравнение третьей степени, благодаря тому, что его левая часть
была представлена в виде произведения множителей, а правая - равна 0.
Слайд 47Что значит представить многочлен в виде произведения?
Какие способы разложения многочлена на
множители вы знаете?
Нет ли на слайде уравнения, левую часть которого можно легко разложить на множители?
Слайд 49Разложим многочлен в левой части уравнения на множители способом группировки.
Ответ: -1;1;8.
Решим
уравнения
х-8=0 или х-1=0 или х+1=0
Получаем
х=8, х=1 ,х= -1.
Слайд 50При решении данного уравнения мы применили один из методов решения целых
уравнений - метод разложения многочлена на множители.
Суть его заключается в следующим:
В уравнении Р(х)=0 многочлен Р(х)разложить на множители и затем прировнять каждый множитель к 0.Решив получившиеся уравнения , находим корни уравнения Р(х)=0.
Слайд 51
Р
Е
Ш
И
Т
Е
У
Р
А
В
Н
Е
Н
И
Я
Какие из уравнений можно решить методом разложения на множители?
Слайд 52Решите уравнения используя разложение многочлена на множители.
является биквадратным.
Биквадратное уравнение является квадратным относительно
Решить его можно используя метод введения новой переменной. , t ≥ 0 Тогда исходное уравнение запишется в виде :
Находим корни и .Решаем уравнения
И .
Немного теории.
Слайд 56
Решим уравнение
Применим метод введения новой переменной для
решения биквадратного уравнения.
Слайд 57НАЙДИТЕ НА СЛАЙДЕ БИКВАДРАТНОЕ УРАВНЕНИЕ И РЕШИТЕ ЕГО.
Слайд 60Метод введения новой переменной применяется при решении не только биквадратных уравнений.
Этим
методом можно решить и такие уравнения, как
Слайд 62Какую замену можно выполнить при решении этого уравнения?
ПРОВЕРИТЬ
Слайд 63
Р
Е
Ш
И
Т
Е
У
Р
А
В
Н
Е
Н
И
Я
У нас на слайде осталось три уравнения.
Слайд 64 Можно выделить целую группу уравнений, которые решить одним из рассмотренных
методом трудно.
И тогда на помощь приходят графики функций.
Слайд 65Решим уравнение
Такой метод решения уравнений называется графическим методом
используя графики функций.
Слайд 66Суть графического метода:
левую и правую части уравнения рассматриваем как две
функции.
В одной системе координат строим графики этих функций.
Находим точки пересечения графиков.
Абсциссы точек пересечения являются корнями уравнения.
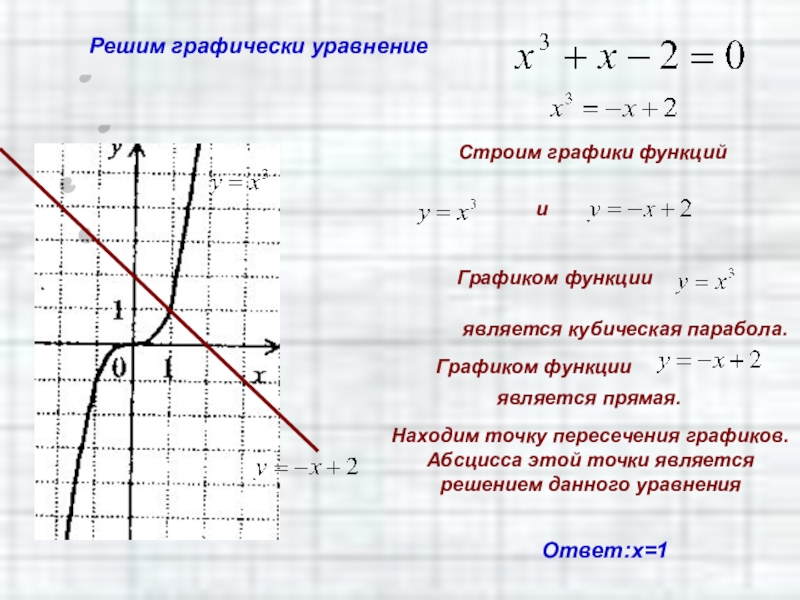
Слайд 67Решим графически уравнение
Ответ:х=1
Находим точку пересечения графиков. Абсцисса этой точки является решением
данного уравнения
Слайд 68 Как вы думаете, в чём недостаток данного метода решения?
Графический способ
решения уравнений не всегда обеспечивает высокую точность результата, и поэтому иногда приходится этот результат уточнять при помощи вычислений.
Слайд 69Итог урока
Какие методы решения целых уравнений мы разобрали на уроке?
Какое уравнение
называется биквадратным?
Сколько корней может иметь биквадратное уравнение?
Сегодня на уроке мы рассмотрели некоторые методы решения целых уравнений.
Слайд 71Домашнее задание
№273(а,д)
№278(а,г)
№276(б)
Провести исследование корней биквадратного уравнения.
Слайд 72У нас остались не решены два уравнения
К сожалению мы разобрали не
все приёмы используемые при решении целых уравнений. Значит нам есть над чем работать на следующем уроке.
Слайд 74Тема урока:
"Решение целых уравнений"
Тип урока: урок отработки навыков.
Вид урока: урок
- практикум.
(2 часа)
Слайд 75Цели урока:
Образовательные: обобщить и углубить сведения об уравнениях; закрепить умения и
навыки решения целых уравнений; систематизировать материал по данной теме.
Развивающие: развитие мыслительной деятельности, внимания, развитие интереса к предмету, формирование потребностей к приобретению знаний.
Воспитательные: воспитывать у учащихся взаимоуважения, трудолюбия, навыков самоконтроля.
Слайд 76ПЛАН УРОКА
Проверка домашнего задания. (Работа с таблицей)
Устная работа. (Математическая эстафета)
Решение задач
на доске и в тетрадях.
Самостоятельная работа.
Практическая работа.
Углубление материала.
Домашнее задание.
Подведение итогов урока. Рефлексия.
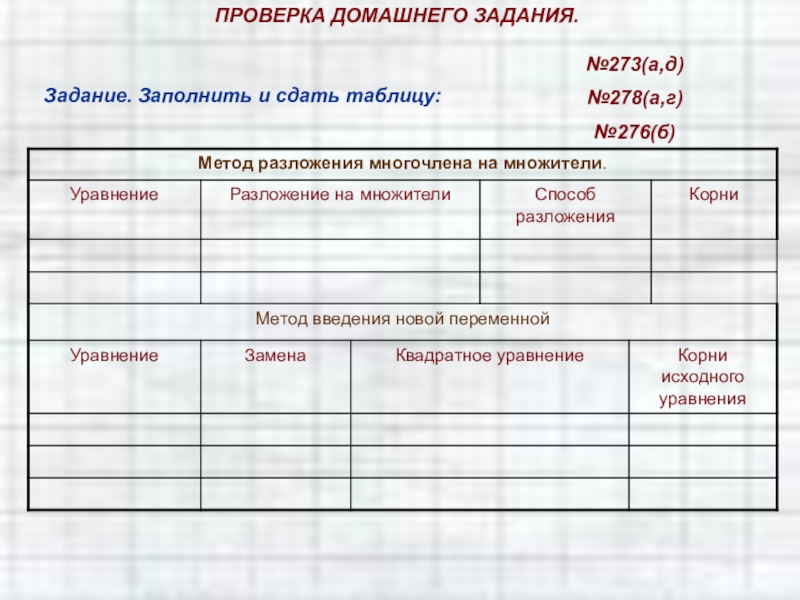
Слайд 77ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ.
Задание. Заполнить и сдать таблицу:
№273(а,д)
№278(а,г)
№276(б)
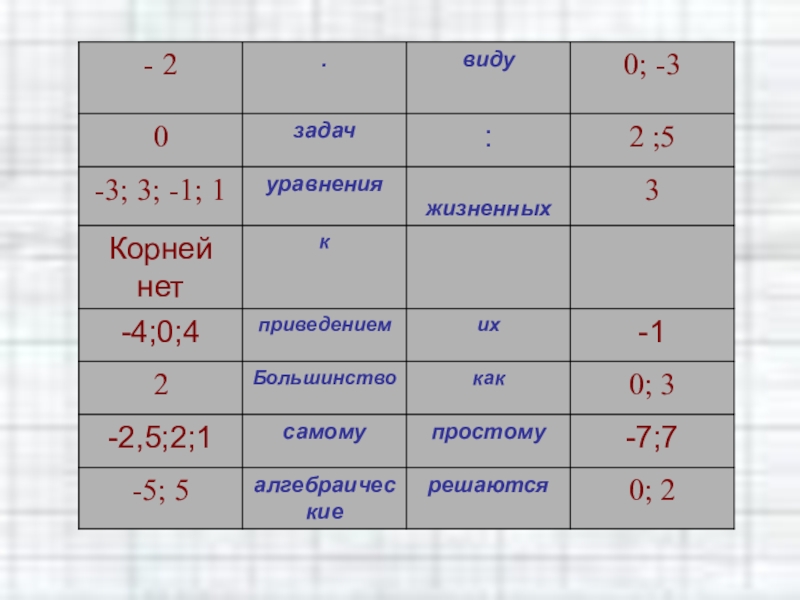
Слайд 78 Игра «Эстафета».
Каждому ряду даются уравнения. Решив их по цепочке и
заменив ответ соответствующим словом из таблицы, можно прочитать эпиграф к нашему уроку.
Слайд 81Вопросы учащимся
Какие уравнения вы сейчас решали?
Какие методы вы применяли при решении?
Какое
уравнение называется биквадратным?
Сколько корней может иметь биквадратное уравнение?
Когда биквадратное уравнение имеет 4 корня?
Когда биквадратное уравнение имеет 3 корня?
Когда биквадратное уравнение имеет два корня?
Когда биквадратное уравнение не имеет корней?
Слайд 82Устная самостоятельная работа
Установите соответствие:
Уравнение → способ
1.
2.
3. 4.
5.
Способы решения:
А. графический способ
Б. разложение на множители способом вынесения общего множителя за скобки
В. Ввести новую переменную, т.е. подстановку: t=…
Г. Разложение на множители способом группировки
Д. Разложение на множители способом вынесения общего множителя за скобки, введением подстановки: t=…
Слайд 83
Ответы
к устной самостоятельной работе
Ответы:
1 → В
2 → Б
3 →
Д
4 → Г
5 → А
Слайд 84Решение уравнений на доске
и в тетрадях.
Слайд 85Выбрав удобную подстановку решите уравнения
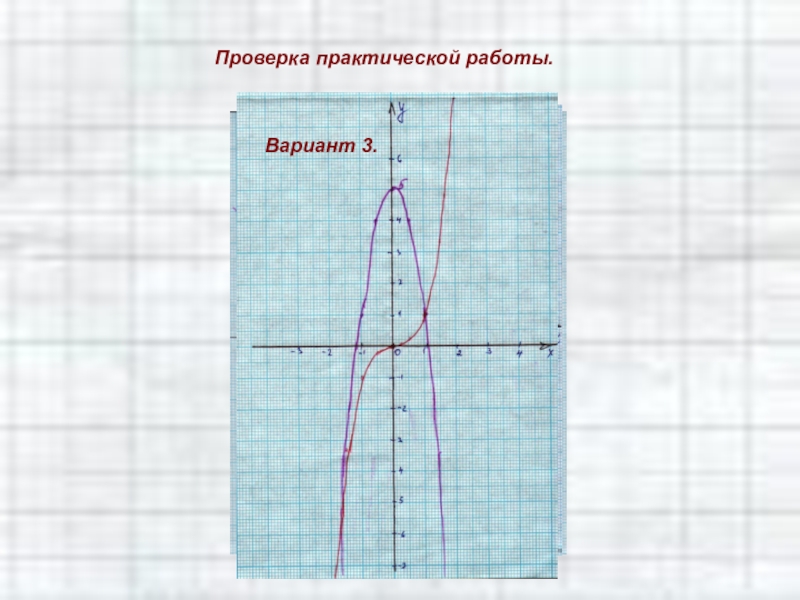
Слайд 86Проведем практическую работу.
У каждого на миллиметровой бумаге задана координатная плоскость
и записано уравнение. Решите эти уравнения графически.
.
1 вариант.
2 вариант.
3 вариант.
Слайд 88Решим задачу №270.
Прочитайте условие задачи и составьте уравнение.
Какое вы получили уравнение?
Решите
полученное уравнение.
Слайд 89
Все ли найденные значения х удовлетворяют условию задачи?
Ответ : 6см.
Проверяем решение.
Слайд 90Решим задачу на нахождение координат точек пересечения графика функции с осями
координат.
№280.(У доски)
АЛГОРИТМ НАХОЖДЕНИЯ КООРДИНАТ ТОЧЕК ПЕРЕСЕЧЕНИЯ.
С осью х:
Решить уравнение f(х)=0
С осью у:
Находим f(0).
Слайд 91№280 решить самостоятельно.
Вариант 1.(б)
Вариант 2.(в)
Проверить
Слайд 92На прошлом уроке у нас остались не решены два уравнения
Сегодня мы
разберём некоторые приёмы решения уравнений высших степеней и решим эти уравнения.
Слайд 93Ни один из рассмотренных методов решения уравнений не подходит для решения
этого уравнения.
Хотя левая часть разложена на множители- правая часть ≠0.
Очевидно, что раскрытие скобок тоже ни к чему не приведёт.
Да и графический метод нам в этом случае не поможет.
Решим уравнение
Слайд 94Для решения уравнений подобных данному можно применить такой приём:
Перемножим по два
множителя так, чтобы коэффициенты перед х были одинакова.
Умножим х на (х+3) и (х+1) на (х+2)
Теперь уравнение легко решить методом введения новой переменной.
Решите это уравнение комментируя решение.
Слайд 97Решим второе уравнение
Получили 4 корня.
Запишите ответ.
Слайд 98Решим уравнение
Это симметрическое уравнение четвёртой степени.
Слайд 99Группируем слагаемые с и .
Выносим -5 за
скобки.
Получаем уравнение
Слайд 101Воспользуемся такой заменой в нашем уравнении.
Получим уравнение
Решив его ,найдем корни
Слайд 104Решим №268.
Что называется корнем уравнения?
Какова область значений этой функции?
Значит, при любых
значениях х , у≥4.
Слайд 105Мы рассмотрели некоторые приёмы решения целых уравнений высших степеней. Чтобы отработать
навыки их применения, предлагаю дома решить два уравнения:
Слайд 106Домашнее задание.
П.12 стрю.83 вопр.1-3.
По вариантам
1 вариант- в
2 вариант- г
№273
№276
№278
Решить №271 и
280 (г)
Для тех. Кто хочет знать больше: №274(а)
Слайд 107Подведём итог урока.
Что нового вы узнали на уроке?
Какие задачи мы сегодня
решали?
Какие способы решения уравнений повторили?
Слайд 108СПАСИБО ЗА УРОК!
УРОК ОКОНЧЕН.
Оцените вашу работу на уроке .
Слайд 109Тема урока: "Решение целых уравнений"
Тип урока: урок закрепления .
Форма урока: урок
–консультация.
Слайд 110Цели урока:
Образовательные: Закрепить знания, умения и навыки при решении уравнений высших
степеней
Развивающие: развитие мыслительной деятельности, внимания, развитие интереса к предмету, формирование потребностей к приобретению знаний.
Воспитательные: воспитывать у учащихся взаимоуважения, трудолюбия, навыков самоконтроля.
Слайд 111
Описание урока:
Урок –консультация представляет собой своеобразную самостоятельную работу, во время которой
ученик может консультироваться с учителем. При этом за каждую консультацию оценка снижается на 0,25 балла.
Для каждого ученика готовятся карточки. В каждой карточке 4 задания. Первое задание направлено на проверку обязательных результатов обучения.
Второе задание– задания обязательного уровня с элементом сложности.
Третье задание- аналогично второму, только уровень сложности увеличен в два раза.
Четвёртое задание – это задание повышенной трудности. Сюда входят упражнения требующие дополнительных знаний, смекалки, неординарного мышления.
Слайд 112Первое задание выполняют все учащиеся.
Если при выполнении задания возникают вопросы, то
ученик может обратится за консультацией к учителю, о при этом снимается 0,25 балла.
Далее учащиеся сами выбирают задания и набирают баллы.
За консультацию второго задания снимается 0,5 балла.
За консультацию третьего задания - 1балл.
4 задание лишено консультации.
Баллы, набранные учащимися, с учётом консультаций, суммируются и выставляется оценка.
Слайд 113Задания на 1балл.
Вариант 1.
Вариант2.
Задания на 2 балла.
Слайд 114Задания на 3 балла.
Вариант 1.
Вариант 2.
Задания на 4 балла
Найдите четыре последовательных
целых числа, произведение которых равно 120.
Найдите четыре последовательных нечётных числа, произведение которых равно 105.
Слайд 115От 4 до 9 баллов – «3»
От 10 до 14 баллов
– «4»
От 15 до 20 баллов – «5»
Критерий оценивания
Слайд 116СПАСИБО ЗА УРОК!
УРОК ОКОНЧЕН.
Оцените вашу работу на уроке .