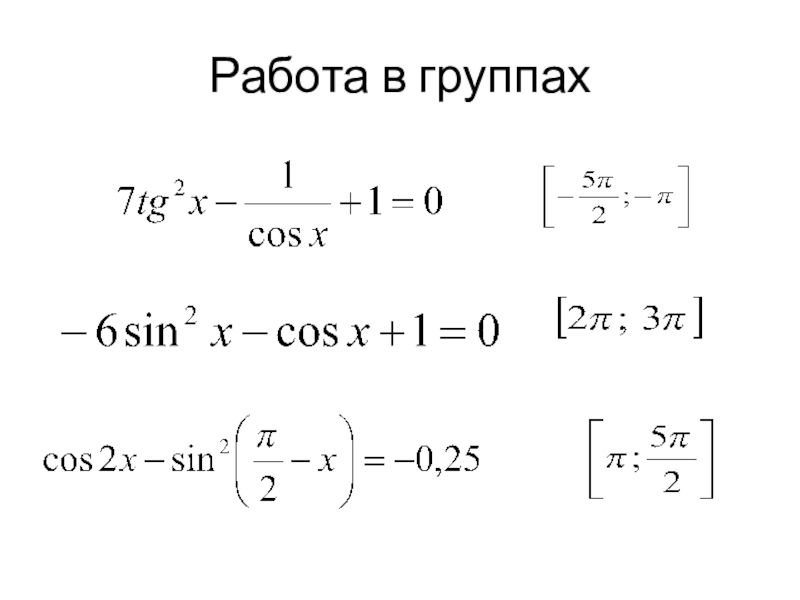(задание №13)»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Урок-практикум по теме Решение тригонометрических уравнений с выбором корней для 11 класса
Содержание
- 1. Презентация Урок-практикум по теме Решение тригонометрических уравнений с выбором корней для 11 класса
- 2. «Учиться можно только весело… Чтобы переваривать знания,
- 3. Цель:систематизация знаний по теме: «Решение тригонометрических уравнений с выбором корней на промежутке»
- 4. «Метод решения хорош тем, что если с
- 5. а). Решите уравнениеб). Найдите все корни этого уравнения, принадлежащие отрезку
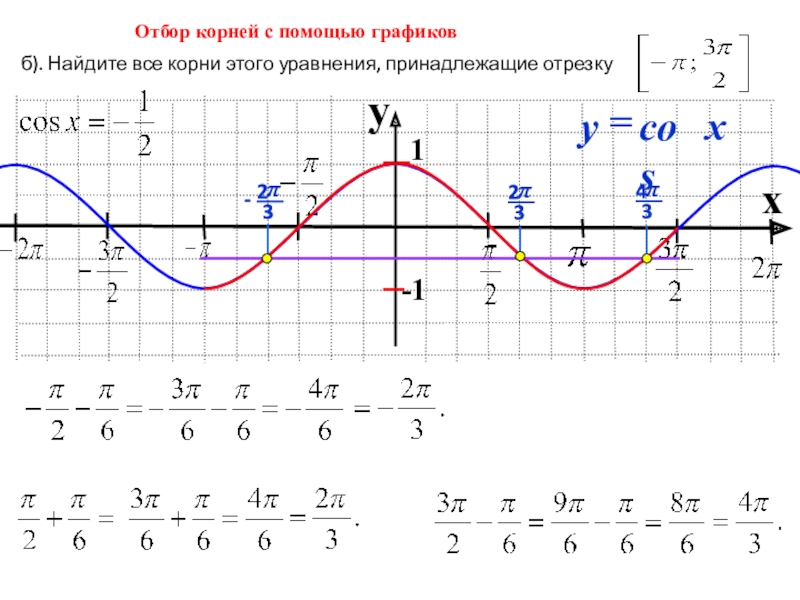
- 6. yx1-1б). Найдите все корни этого уравнения, принадлежащие отрезку Отбор корней с помощью графиков
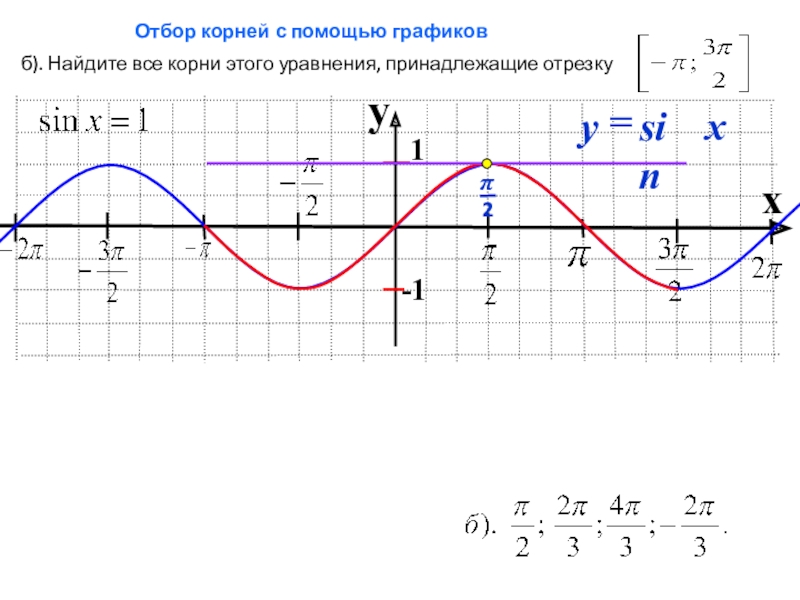
- 7. yx1-1б). Найдите все корни этого уравнения, принадлежащие отрезку Отбор корней с помощью графиков
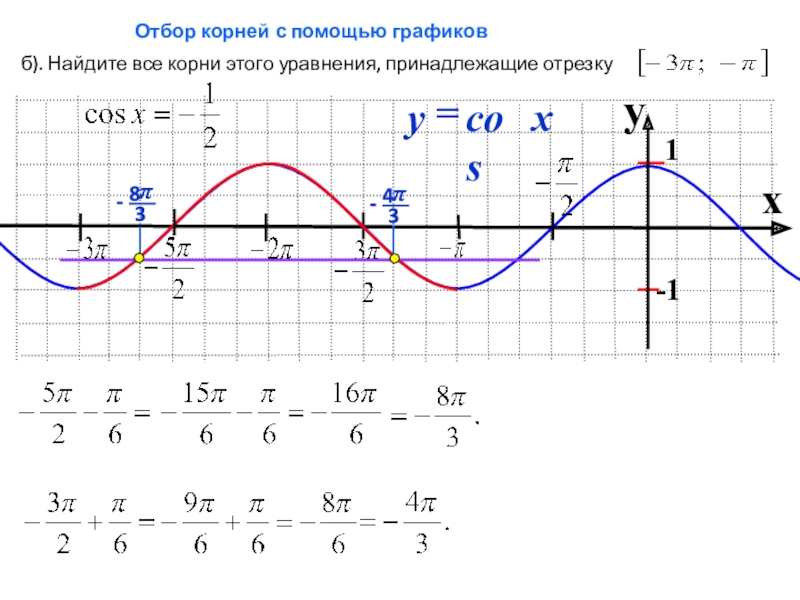
- 8. xб). Найдите все корни этого уравнения, принадлежащие отрезку Отбор корней с помощью графиков
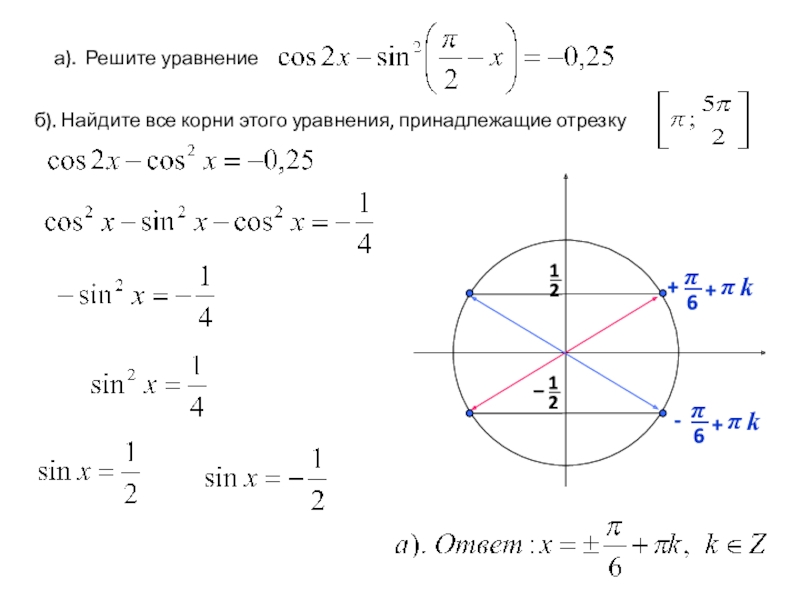
- 9. а). Решите уравнениеб). Найдите все корни этого уравнения, принадлежащие отрезку
- 10. Слайд 10
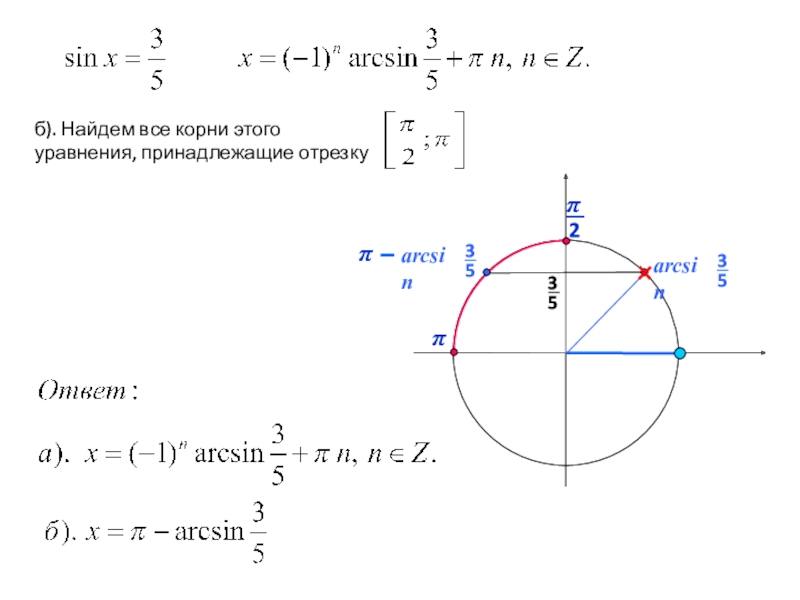
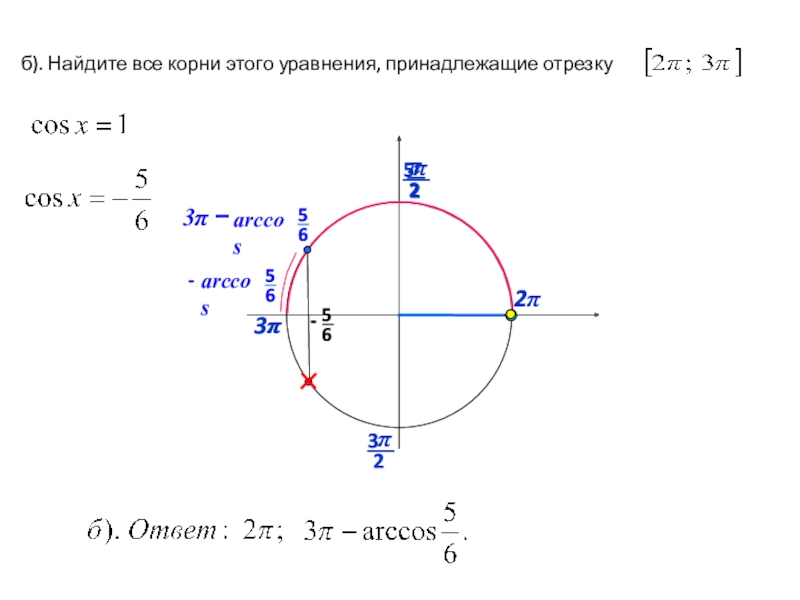
- 11. а). Решите уравнениеб). Найдите все корни этого
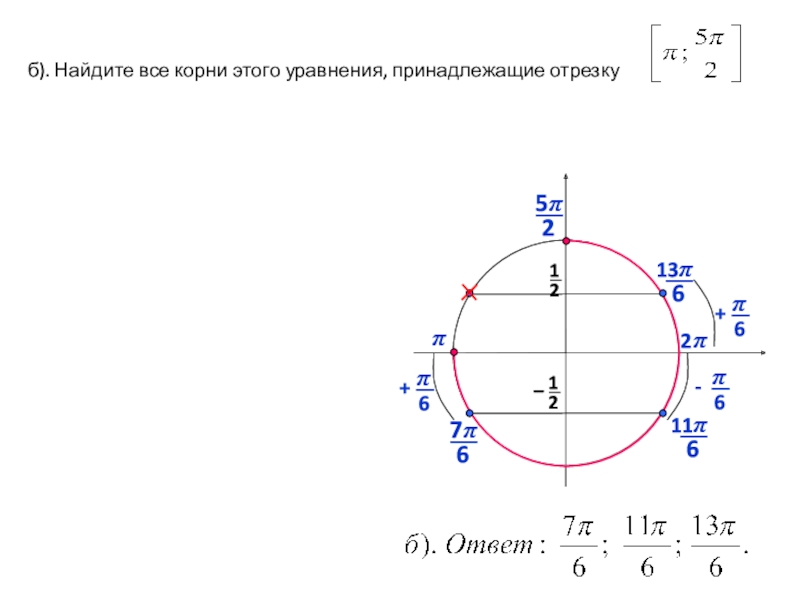
- 12. б). Найдите все корни этого уравнения, принадлежащие
- 13. Работа в группах
- 14. 1 группа
- 15. а). Решите уравнениеб). Найдите все корни этого уравнения, принадлежащие отрезку
- 16. б). Найдите все корни этого уравнения, принадлежащие
- 17. 2 группа
- 18. а). Решите уравнениеб). Найдите все корни этого уравнения, принадлежащие отрезку p или
- 19. 2ppб). Найдите все корни этого уравнения, принадлежащие отрезку 3p
- 20. 3 группа
- 21. а). Решите уравнениеб). Найдите все корни этого уравнения, принадлежащие отрезку
- 22. б). Найдите все корни этого уравнения, принадлежащие отрезку p
- 23. Решение тригонометрического уравнения с последующим выбором корней
- 24. «Вы - талантливые дети! Когда – нибудь
«Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом»
Слайд 2«Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с
аппетитом»
Анатоль Франс
(1844-1924)
Слайд 3Цель:
систематизация знаний по теме:
«Решение тригонометрических уравнений с выбором корней на
промежутке»
Слайд 4«Метод решения хорош тем, что если с самого начала мы можем
предвидеть и впоследствии подтвердить это, то, следуя этому, мы достигнем цели»
Вильгельм Лейбниц
Слайд 6y
x
1
-1
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с
помощью графиков
Слайд 7y
x
1
-1
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с
помощью графиков
Слайд 8x
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с
помощью графиков
Слайд 11а). Решите уравнение
б). Найдите все корни этого уравнения, принадлежащие отрезку
б).
Выбирать корни по тригонометрической окружности не удобно, т.к. это … полтора круга
Слайд 23Решение тригонометрического уравнения с последующим выбором корней из заданного промежутка эксперты
оценивают выполнение задания по следующим критериям:
- обоснованно получены ответы в обоих пунктах – 2 балла (это макс. балл);
- обосновано решение в пункте а или б –
1 балл;
- решение не соответствует ни одному из критериев, перечисленных выше – 0 баллов.
Слайд 24«Вы - талантливые дети! Когда – нибудь вы сами приятно поразитесь,
какие вы умные, как много вы сумеете, если будете постоянно работать над собой…»
Жан-Жак Руссо